Магнитная сборка Халбаха — особая конфигурация постоянных магнитов, характеризующаяся тем, что магнитное поле с одной из её сторон практически полностью отсутствует благодаря особому расположению элементов сборки. В этой задаче мы исследуем это явление.

Магнитные диполи

Диполем называется точечный магнитный элемент (например, маленькая петля с током. Ее дипольный момент $I\vec S$, где $I$ — это ток, бегуший по петле, a $\vec S$ — ориентированная площадь). Поле, создаваемое магнитным диполем, описывается следующей формулой: $$\vec B (\vec r) = \frac {\mu_0}{4\pi} \left(\frac{3\vec r (\vec m \cdot \vec r )} {r^5} - \frac { \vec m} {r^3}\right), $$ где $m$ — дипольный момент, $\vec r$ — радиус-вектор точки в пространстве относительно диполя. $\mu_0=4\pi\cdot 10^{-7}~\text{Гн/м}$. На рисунке изображены диполь, вектор и угол между ними.

A1  ^0.50 Магнитное поле ослабляется с увеличением расстояния, для заданного угла $\theta$ найдите зависимость магнитного поля $B$ на расстоянии $r$ от диполя.

Магнитная шайба

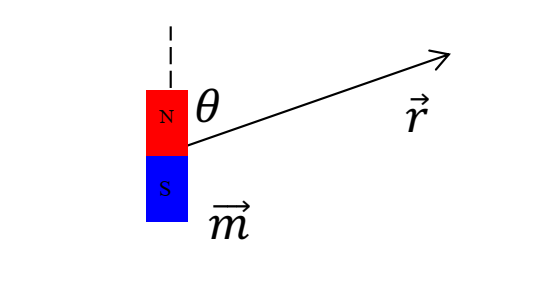
Рассмотрим лёгкий магнит, представляющий собой плоский цилиндр радиуса $R$ и толщиной $h \ll R$ c поверхностной плотностью магнитного момента $\vec\sigma$. Вектор поверхностной плотности ориентирован вдоль оси диска.

B1  ^1.50 Выразите магнитное поле $B(y)$ вдоль оси, перпендикулярной магниту, на расстоянии $y$ от центра.

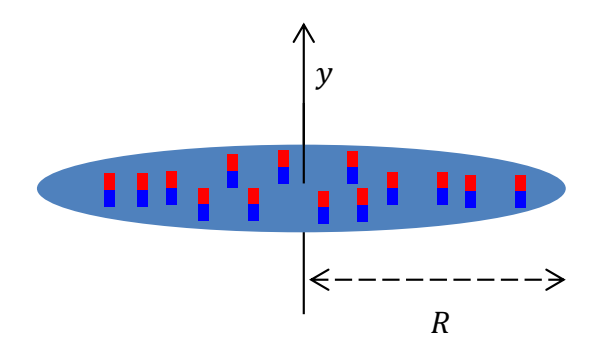
Если приблизить маленький круглый магнит к металлической двери холодильника, магнит притягивается к ней с силой, зависящей от размеров и типа материала магнита, а также толщины двери. В этом пункте считайте толщину двери много большей линейных размеров магнита. Рассмотрим цилиндрический магнит с объемной плотностью дипольного момента $\rho = 1.05 \cdot 10^6 \frac {\text{ Тл} \cdot \text{м}}{\text{Гн}}$ толщиной $t=2~\text{мм}$ и диаметром $D=20~\text{мм}$.

B2  ^0.50 Оцените величину магнитного поля вблизи поверхности магнита. Ответ выразите через величины $t,~D,~\rho,~\mu_0$.

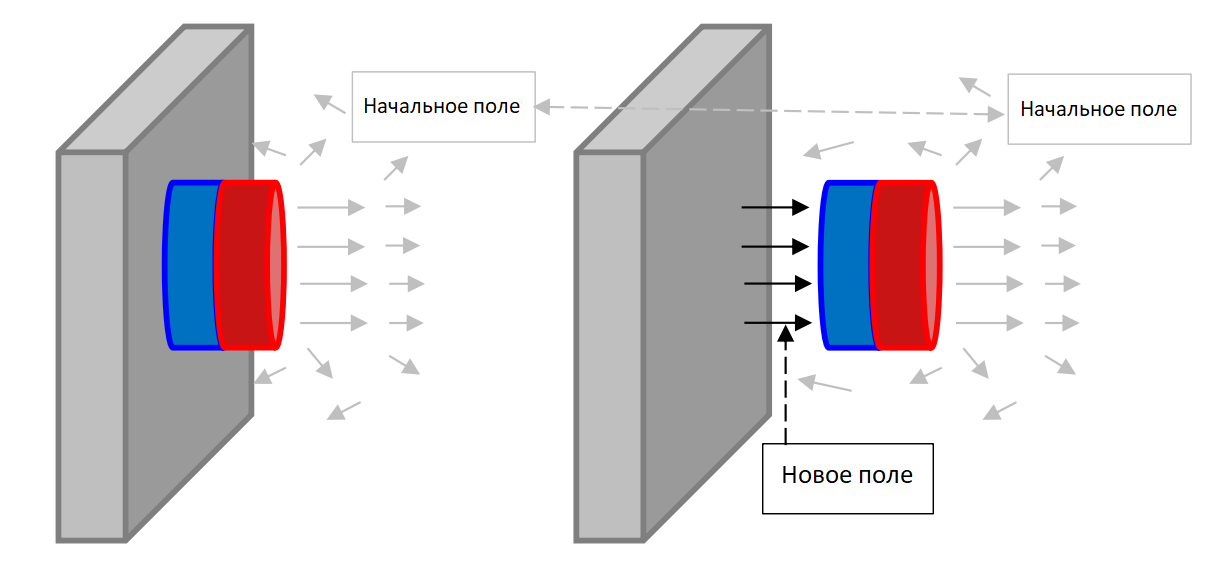
Чтобы определить силу взаимодействия магнита и двери холодильника, необходимо воспользоваться законом сохранения энергии. Когда магнит отрывают от двери, между ними возникает поле, приблизительно равное полю с другой стороны магнита. Остальная часть поля (включая и то, что внутри двери) почти не меняется. Выражение для объёмной плотности энергии магнитного поля в воздухе: $w=\frac{B^2}{2\mu_0}$.

B3  ^0.50 Получите выражение и численное значение силы взаимодействия $F_0$ между дверью и прижатым к ней магнитом, также вычислите давление $P_0$ магнита на дверь.

Магнитная сборка Халбаха

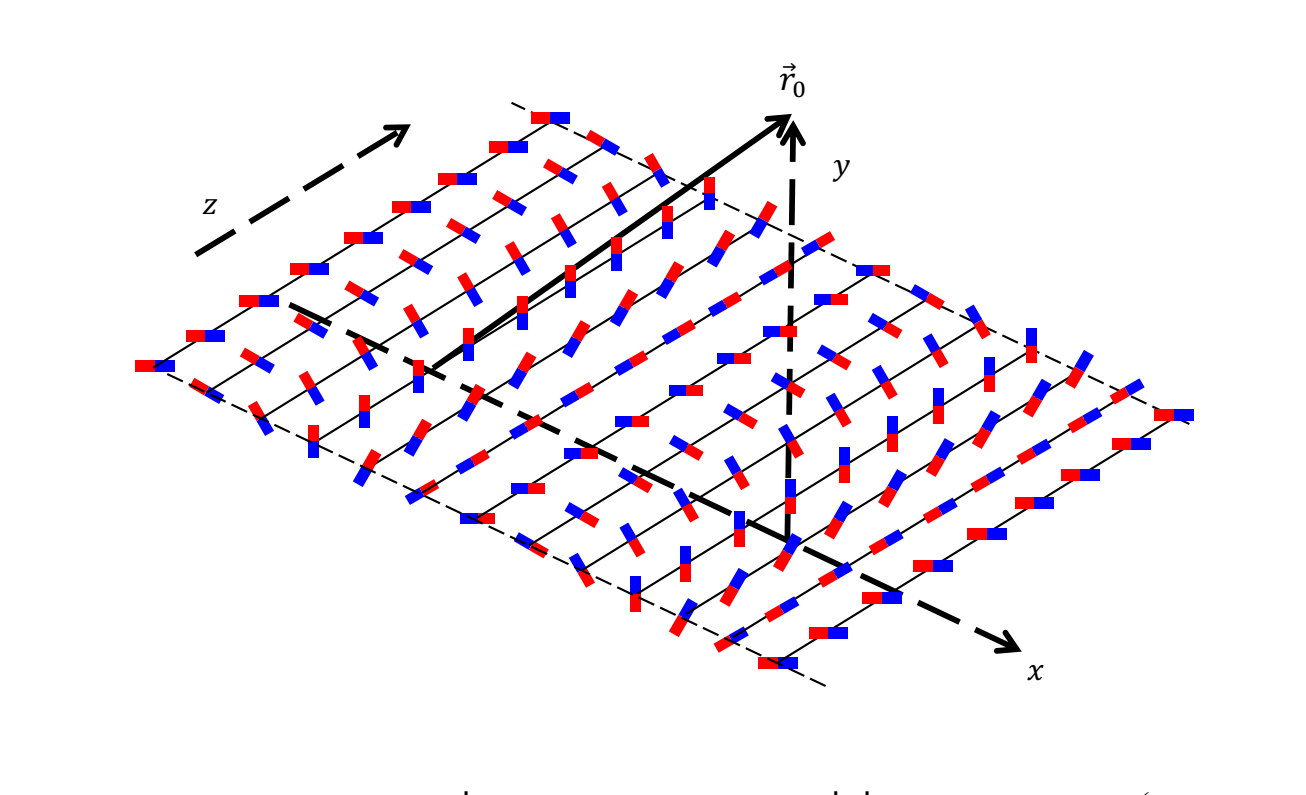
Для того чтобы получить выражение магнитного поля в сборке Халбаха, найдем поле длинного ряда магнитов, как показано на рисунке. Линейная плотность дипольного момента ряда $\rho_L$, направление — вдоль оси $y$.

C1  ^2.00 Запишите выражение для поля $\vec B(\vec r_0, y)$ которое создает ряд магнитов. (Для удобства поле выражается и через $\vec r_0$, и через $y$, хотя технически $y = (\vec r_0)_y$.)

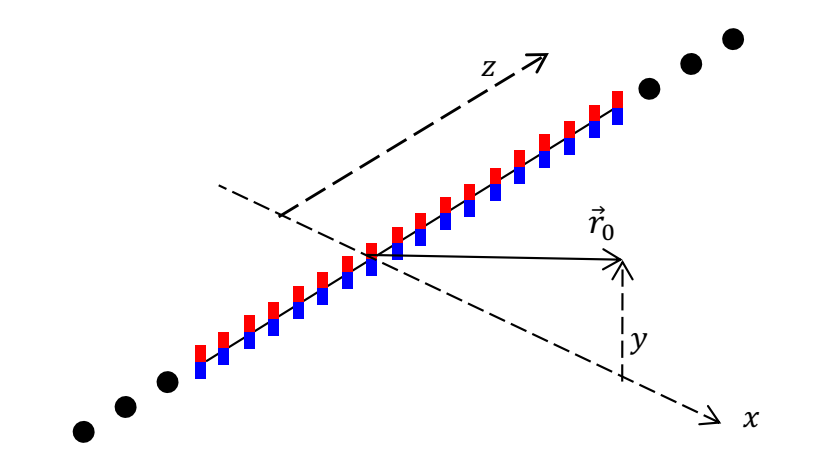
В плоской магнитной сборке Халбаха направление поляризации маленького элемента площади непрерывно вращается. Его положение меняется в соответствии с формулой: $$\beta(x,z)=\beta_0+k\cdot x,~k=2\pi/\lambda,~ t\ll\lambda$$ Здесь $\beta$ — это угол между направлением диполя и перпендикуляром к плоскости, этот угол вращается в плоскости $xy$. Длина $\lambda$ — это шаг сборки, а $t$ — толщина сборки.

C2  ^1.00 Найдите магнитного поля с двух сторон от сборки. Ответ дать в виде некоторого интеграла.

Один из этих интегралов нужен для решения этого пункта: $$ \int_{-\pi/2}^{\pi/2} dx\cdot\cos(2x)\cdot\cos(c\cdot\tan x)=\frac{c \cdot \pi} {e^c}=\int^{\pi/2}_{-\pi/2}dx\cdot\sin(2x)\cdot\sin(c\cdot\tan x) $$ $$ \frac{\pi}{e^d} = \int_{-\infty}^{\infty} dx\cdot\frac{\cos x}{d^2+x^2} $$ $$ \frac{\pi}{a\cdot e^a}= \int^{\infty}_{-\infty} dx\cdot \frac {2x\cdot\sin(2x)} {(a^2+x^2)^2} $$ $$ \frac {(b+1)\pi}{e^b}= \int^{\infty}_{-\infty}dx \cdot \frac{2b^3x\cdot \cos(x)}{(b^2+x^2)^2} $$

C3  ^1.00 Покажите, что с одной стороны идеальной сборки магнитное поле стремится к нулю.

C4  ^1.00 Запишите выражение для поля с другой стороны.

C5  ^1.50 На основании выражения поля найдите среднее давление $Р$ такого магнита на дверь холодильника. Возьмите следующие параметры: толщина $t=0.5~\text{мм}$, объемная плотность магнитного диполя $\rho = 2 \cdot 10^5 \frac {\text{Тл} \cdot \text{м}} {\text{Гн}}$, шаг сборки $\lambda=5~\text{мм}$.

C6  ^0.50 Найдите соотношение между давлением, которое создает магнитная сборка Халбаха и давлением, которое создает обычный магнит из того же материала, с теми же радиусом и толщиной. Здесь тоже следует пренебречь эффектами на периметре кружка и и толщиной магнита.

Вы могли подумать, что ни в чем более инновационном, чем магнитики для холодильника, сборка Халбаха не применяется. Однако компания Hendo разработала на ее основе разработала целый ховерборд (тот самый, что был в фильме <<Назад в будущее>>). Используя кольцевую сборку Халбаха из электромагнитов, Hendo добились подъемной силы достаточной, чтобы заставить человека средней массы подняться над землей! Но только над медью.