A1  ^0.20 Запишите уравнение колебаний бруска без учета трения и внешних сил в виде
$$
\ddot{x} + \omega_0 ^2 x + \varepsilon x^3 = 0.
$$
Укажите численные значения частоты свободных гармонических колебаний малой амплитуды $\omega_0$ и параметра нелинейности $\varepsilon$.

Уравнение колебаний
$$
I \ddot{x} = - k_1 x - k_3 x^3
$$

A2  ^1.00 Снимите зависимость периода от амплитуды колебаний $T(A)$. Опишите методику (какие начальные условия и времена использовали, по каким формулам определяли период). Исследуйте диапазон амплитуд, при которых период меняется не более чем на 10%. Проведите не менее 15 измерений при различных значениях амплитуды.

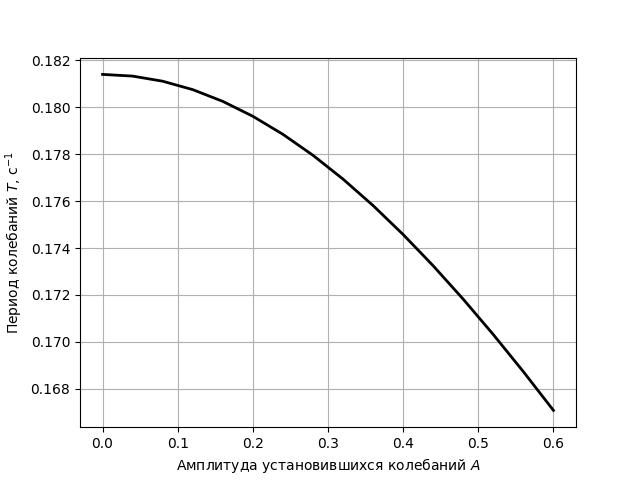
Зададим в качестве начального условия $x_0 = A, \; v_0 = 0$, тогда амплитуда колебаний будет равна $A$. Период колебаний можно определить, измерив положение одного из следующих максимумов или нулей зависимости $x(t)$. График зависимости периода от амплитуды приведен выше.

A3  ^0.80 При достаточно малых амплитудах зависимость периода от амплитуды имеет вид
$$
T = T_0 (1 + \alpha A^n).
$$
Здесь $T_0$ — период колебаний малой амплитуды.
Определите из ваших данных параметры $\alpha$, $n$.

Построим график зависимости $\ln( (T_0 -T)/T_0)$ от $\ln A$. Из него найдем

Заметим, что квадратичная зависимость периода от амплитуды работает тем точнее, чем меньше амплитуда. Если использовать слишком большие амплитуды, эффективное значение показателя степени окажется меньше.

A4  ^1.50 При достаточно малой амплитуде колебаний зависимость угла от времени имеет вид
$$
x = a \cos \omega t + b \cos 3 \omega t.
$$
Исследуйте зависимость амплитуды гармоники утроенной частоты $b$ от амплитуды колебаний $A$. Исследуйте ту же область амплитуд $A < 0.5$ и определите как можно точнее значение $b$ для 5 различных амплитуд.

\textit{Примечание:} Исследуемый эффект достаточно мал. Убедитесь, что вы проводите вычисления и измерения с достаточной точностью, чтобы его качественно наблюдать. При необходимости вы можете уменьшить шаг по времени для численного решения.

Используя формулу $\cos 3 \omega t = 4 \cos^3 \omega t - 3 \cos \omega t$, представим зависимость координаты от времени в виде
$$
x = (a - 3 b) \cos \omega t + 4 b \cos^3 \omega t.
$$
Таким образом, зависимость $x/\cos \omega t$ от $\cos^2 \omega t$ линейна, причем коэффициент наклона графика равен $4b$. Для линеаризации нужно точно знать значение частоты колебаний при данной амплитуде $A = a + b$. При этом можно считать $b \ll a$, поэтому $a \approx A$.
Для амплитуд $A = 0.1;\, 0.2;\, 0.3;\, 0.4 ;0.5.$ точно измеряем несколько точек на первой четверти периода зависимости $x(t)$ и получаем отсюда значения $b$.

A5  ^0.50 Известно, что при малых амплитудах $b = \beta A^3$. Определите по вашим данным коэффициент $\beta$.

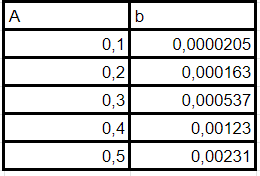
Построим график найденной в прошлом пункте зависимости в координатах, в которых она линейна (например $b$ от $A^3$). Отсюда найдем $
\beta = 0.019
$.

Для сравнения теоретическое значение $\beta = \varepsilon /32 \omega_0^2 \approx 0.0208$. Отличие связано в первую очередь с тем, что при конечных амплитудах нужно учитывать поправки высшего порядка, которые при $A = 0.5$ уже не совсем пренебрежимы.

B1  ^1.00 Как можно точнее определите значения $\omega_0$, $\varepsilon$, $\gamma$.

Значение $\omega_0 = 2\pi/T_0$ можно найти, измерив период свободных колебаний (положив величину внешнего момента равной нулю), а коэффициента $\gamma$ — по затуханию колебаний (нужно выбрать амплитуду колебаний так, чтобы их можно было считать линейными). Амплитуда колебаний зависит от времени как $A = A_0 e^{- \gamma t}$, $\gamma = - \frac{1}{t} \ln \frac{A}{A_0}$.

Для определения коэффициента перед нелинейным слагаемым приложим силу нулевой частоты (то есть постоянную) и найдем установившееся значение смещения $A$. Тогда $\varepsilon = \frac{f - \omega_0 A}{A^3}$.

B2  ^1.50 Выберем значение $f = 25 ~\text{c}^{-2}$. Постройте графики зависимости амплитуды колебаний и сдвига фаз от частоты. Для сравнения на тех же графиках постройте аналогичные теоретические зависимости без учета нелинейности.

Будем задавать различные значения частоты внешнего момента и измерять отвечающие им значения амплитуды колебаний и фазы. Измерить амплитуду можно непосредственно. Для измерения фазы точно определим положения нескольких максимумов по времени $t_n$.
Зависимость смещения от времени имеет вид
$$
x = A \cos \omega (t - t_n),
$$
поэтому фаза колебаний равна $\varphi = - \omega t_n$. Вычитая отсюда целое кратное $2 \pi$ можно получить фазу в указанном в условии диапазоне. Строим графики полученных зависимостей и видим, что из-за нелинейности положение резонансного максимума сместилось в область больших частот, а его форма деформировалась.

B3  ^1.00 Выберите значение $f = 80 ~\text{c}^{-2}$. Постройте график зависимости амплитуды результирующих колебаний от частоты. Укажите область частот, в которой наблюдается гистерезис (то есть два значения амплитуды при одной и той же частоте).

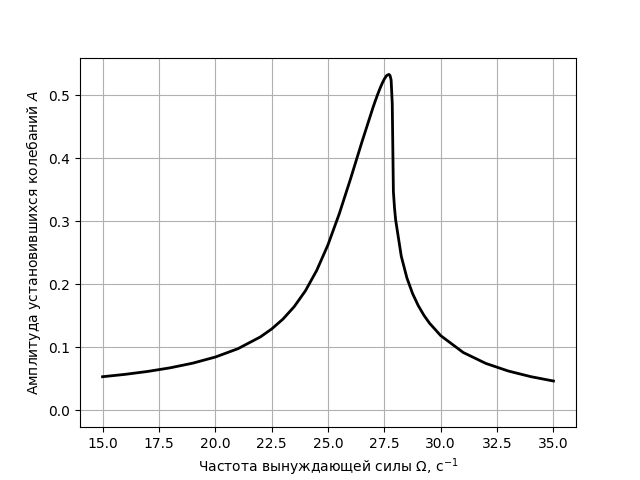
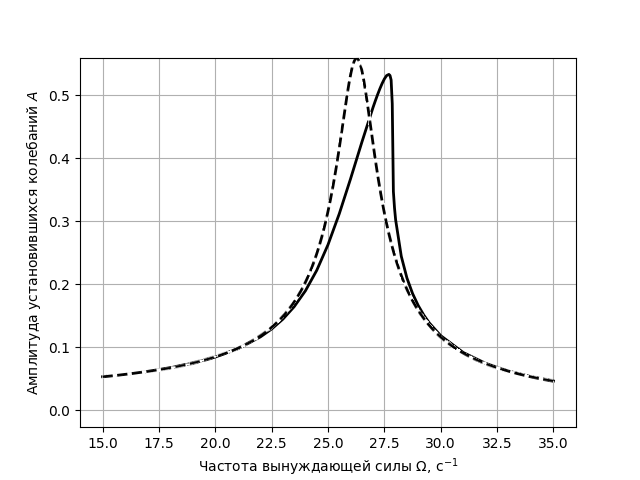
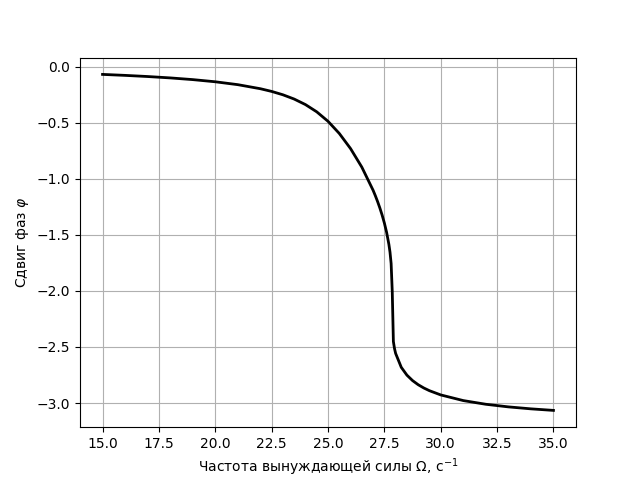
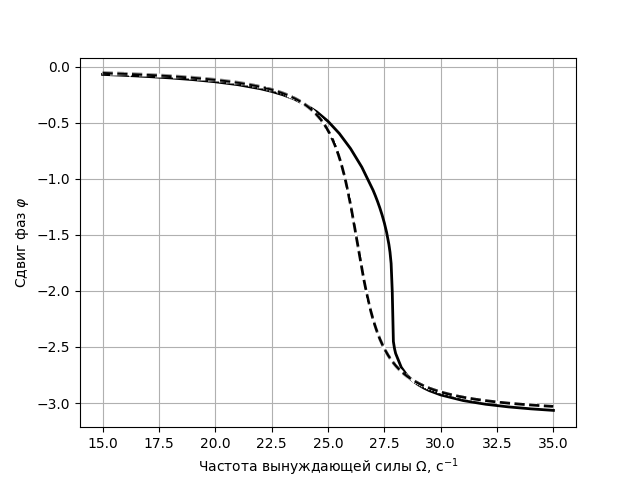
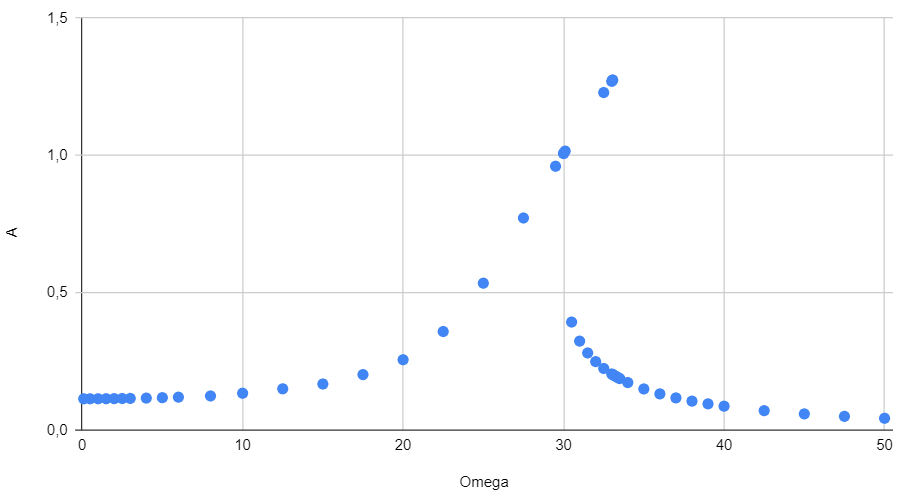
Аналогично предыдущему пункту измеряем зависимость амплитуды от частоты. Если идти в сторону увеличения частоты колебаний (и использовать большое значение $x_0$), можно заметить, что при некоторой частоте амплитуда изменяется скачком. Если же идти со стороны больших частот и использовать маленькие начальные $x_0$, то амплитуда при некоторой частоте увеличится скачком. При этом будет область частот, в которой в зависимости от начальных условий будет два возможных значения амплитуды. При значении $f$ из условия эта область примерно $\Omega \in [30.5,\, 33] ~\text{с}^{-1}$.

С1  ^1.00 Наиболее быстрый рост амплитуды колебаний наблюдается при частоте $\Omega \approx 2 \omega_0$.
Определим отклонение от резонансной частоты $\delta = \Omega - 2 \omega_0 $.
Амплитуда колебаний будет возрастать, если $\delta$ не слишком велико.
На плоскости $\delta$, $\mu$ изобразите область, где амплитуда колебаний растет.
Рассматривайте область $\mu \ll 1$, $\delta \ll \omega_0$.

Будем задавать различные значения $\delta $ (а значит и $\Omega$) и $\mu$. В области вблизи резонанса хорошо виден экспоненциальный рост амплитуды, а при больших отклонениях по частоте амплитуда периодически меняется.
Для каждого значения $\mu$ можно подобрать соответствующую граничную частоту и таким образом построить границу области резонанса.

С2  ^0.50 Определите уравнение для границы области $\delta(\mu)$. Запишите уравнение и найдите его параметры.

Из рисунка в предыдущем пункте видно, что граница имеет вид двух прямых. Измерив на этих прямых координаты нескольких точек, найдем их уравнения.

C3  ^1.50 В области параметрического резонанса зависимость амплитуды от времени имеет вид $A \sim e^{s t}$. Определите зависимость параметра $s$ от относительного изменения частоты $\mu$ и отстройки по частоте $\delta$. Используя численные данные, найдите форму зависимость $s(\mu,\, \delta)$ и определите ее параметры.

Подсказка: может быть полезным изучить зависимость $s (\mu)$ при постоянной частоте $\delta$ для нескольких значений $\delta$. При этом зависимость $s^2$ от $\mu^2$ имеет очень простой вид.

При нескольких значениях $\delta$ построим графики зависимости $s^2$ от $\mu^2$. Видим, что эти зависимости линейны, причем коэффициенты наклона графиков одинаковы (и равны $\omega_0^2/4 = 100 ~\text{c} ^{-1}$), а постоянный член равен $- \delta ^2$.

С4  ^1.00 Амплитуда колебаний растет также и вблизи области $\Omega \approx \omega_0$, при достаточно малых $\delta = \Omega - \omega_0$. Найдите границы области, при которой возможен рост амплитуды $\delta ( \mu)$. Изобразите эту область на плоскости $\delta$, $\mu$. Определите уравнение этой границы. (Подсказка: зависимость $\delta (\mu)$ имеет степенной вид.)

Аналогично части C1 наблюдаем, что есть область, в которой амплитуда колебаний экспоненциально растет. Границы этой области теперь не прямые. Измерив на них координаты несколько точек убеждаемся, что границы — параболы. Их уравнения имеют вид $\delta = \mu^2 \omega_0/32$ и $\delta = - 5 \mu^2 \omega_0 /32$

С5  ^0.50 Пусть $\gamma = 0.2 ~\text{c}^{-1}$, $\varepsilon = 450 ~ \text{c} ^{-2}$. Нарисуйте на плоскости $\mu$, $\delta = \Omega - 2 \omega_0$ область, в которой амплитуда колебаний растет. Для $\delta = 0$ и $\mu = 0.05$ найдите амплитуду установившихся колебаний, а также время оцените время, за которое они устанавливаются.

Амплитуда будет расти, если скорость роста за счет модуляции частоты будет выше скорости затухания за счет трения, то есть $s > \gamma$.
Значит эта область ограничена гиперболой
$$
\mu^2 \omega_0^2/4 - \delta^2 > \gamma^2.
$$
Это можно понять из результата пункта C3 или наблюдать численно.
Рост амплитуды колебаний наблюдается, только если начальная амплитуда достаточно мала. При заданных в условии параметрах устанавливается значение установившейся амплитуды колебаний $A \approx 0.13$ за время $t \approx 50 ~\text{с}$ (точное время зависит от начальных условий).

D1  ^1.00 В случае $\gamma = \omega_0/ 2$ найдите минимальное значение $f_0$, при котором возможно такое движение. (Начальный угол отклонения и начальную угловую скорость маятника считайте равными нулю.)
При $f- f_0 \ll f_0$ зависимость средней угловой скорости от приложенного момента имеет вид $\langle \omega \rangle \sim (f - f_0)^\alpha$. Найдите значение постоянной $\alpha$.

Увеличивая значение $f$ заметим, что линейный рост угла отклонения начинается с $f_0 = 400 ~\text{с}^{-2}$. (Можно и теоретически показать, что рост начинается с $f_0 = \omega_0^2$.)
Снимем зависимость средней частоты от $f$ вблизи порогового значения $f_0$.
Заметим, что угловая скорость скачком приобретает конечное значение $\langle \omega \rangle \approx 10 c^{-1}$ и достаточно слабо зависит от приложенной силы. Поэтому показатель степени $\alpha \approx 0$