A1  ^0.20 Выразите теоретически $F_\min$ и $F_\max$ через $D_\text{сф}$ и $D_\text{ц}$.

Лучи из пучка, падающего в разные точки одного из выделенных диаметров, преломляются и цилиндрической линзой, и сферической, и оптические силы линз складываются: $\cfrac {1}{F_{min}}=\left(D_{\text{сф}}+D_{\text{ц}}\right)$. На ходе другого пучка лучей цилиндрическая линза не сказывается, и фокусировка осуществляется только сферической линзой: $\cfrac {1}{F_{max}}=D_{\text{сф}}$. Таким образом, $F_{min}=\dfrac{1}{D_{\text{сф}}+D_{\text{ц}}},\ F_{max}=\dfrac{1}{D_{\text{сф}}}$.

A2  ^0.40 Для каждой линзы экспериментально определите положения двух ее выделенных направлений. С помощью рисунков и схем объясните, как вы это делаете.

Располагая за освещаемой фонариком линзой экран на различных расстояниях, будем получать различные формы светлых пятен. Видим, что для каждой из линз все возникающие формы пятен симметричны относительно двух перпендикулярных осей, наклоненных под $45^{\circ}$ к горизонту. Это и есть выделенные направления. Таким образом, для всех линз выделенные направления проходят под углами $45^{\circ}$ и $135^{\circ}$.

\textit{Для справки.} Если представлять каждую из астигматических линз как совокупность некоторой сферической и некоторой \textit{собирающей} цилиндрической, то при сборке линз поддерживались следующие направления осей собирающих цилиндров относительно закрепленных на линзах транспортиров: линза №1 – $\left(135\pm5\right)^{\circ}$, линза №2 – $\left(45\pm5\right)^{\circ}$, линза №3 – $\left(45\pm5\right)^{\circ}$.

A3  ^0.40 Определите, какая из трех линз эквивалентна цилиндрической линзе (т.е. имеет $D_\text{сф}=0$). Запишите номер этой линзы в лист ответов, а также приведите обоснование вашего выбора.

Лучи, падающие в разные точки одного из выделенных диаметров цилиндрической линзы, не преломляются, и отвечают за размер светового пятна на экране, измеренный в соответствующем выделенном направлении. По мере удаления экрана от линзы этот размер должен увеличиваться синхронно (по подобию) с увеличением диаметра тени от оправы линзы. В эксперименте такое подобие наблюдается для линзы №2, поэтому она и является цилиндрической.

A4  ^2.00 Для каждой линзы экспериментально определите фокусные расстояния для двух ее выделенных направлений: $F_\min$ и $F_\max$. В листе ответов необходимо подробно описать последовательность действий и измерений, с приведением схем использующихся установок и указанием всех применяемых элементов. Рассчитайте пары значений $D_\text{сф}$ и $D_\text{ц}$. Все полученные числа занесите в таблицу в листе ответов.

Перечислим методы, которыми можно определить фокусные расстояния линзы №1. Во-первых, можно при различных расстояниях между фонариком и линзой подбирать положение экрана так, чтобы видеть на нем четкое изображение (наклонный отрезок), а после этого с помощью формулы тонкой линзы (и линеаризации для увеличения точности) рассчитать одно из фокусных расстояний. Второе фокусное расстояние оказывается слишком большим, чтобы соответствующая установка помещалась на парте. Во-вторых, можно стараться получить четкие изображения на удаленной стене, тогда два различные расстояния между фонариком и линзой будут примерно равны фокусным расстояниям линзы. В-третьих, можно заметить, что одной из комбинаций линз №2 и №3 можно получить сферическую линзу, т.е. создать параллельный пучок света круглого сечения. Параллельность можно проверить, получая на экране одну и ту же форму светового пятна при всех положениях экрана в этом параллельном пучке. Тогда внесение линзы №1 в параллельный пучок позволит наблюдать четкие изображения на экране при двух его положениях, соответствующих фокусам. Возможны и другие экспериментальные способы определения фокусных расстояний.

Описанные для линзы №1 первые два метода применимы также для нахождения одного из фокусных расстояний линзы №2 (второе ее фокусное расстояние равно бесконечности, исходя из результата п. A3).

Одно из фокусных расстояний линзы №3 находится любым из перечисленных выше методов. Другое фокусное расстояние третьей линзы отрицательное (линза рассеивает), его удобно найти, если совместить линзу с одной из первых двух для получения собирающей сферической линзы, а дальше использовать один из названных методов и уже найденные величины для первых двух линз.

Результаты измерений и расчетов занесены в таблицу ниже. Отметим, что каждую из линз №1 и №3 можно представлять как совокупность сферической и либо собирающей цилиндрической, либо рассеивающей цилиндрической. В зависимости от этого выбора могут получаться различные ответы для величин $D_{\text{сф}}$ и $D_{\text{ц}}$, поэтому в таблице приведены различные возможные комбинации, все их можно считать соответствующими действительности.

	линза №1	линза №2	линза №3
$F_\min$, см	17	25	-100
$F_\max$, см	50	$(\infty)$	33
$D_\text{сф}$, дптр	2 или 6	0	3 или -1
$D_\text{ц}$, дптр	4 или -4	4	-4 или 4

B1  ^0.30 Соберите установку, в которой на линзу №1 свет падает параллельным пучком с круговым поперечным сечением. В листе ответов зарисуйте схему установки и обозначьте все использованные элементы. Опишите, как вы контролируете параллельность пучка.

Одна из комбинаций линз №2 и №3 образует сферическую линзу, на которую можно светить расположенным в ее фокусе фонариком для получения параллельного пучка. Как упоминалось выше, параллельность можно проверить, получая на экране одну и ту же форму светового пятна при всех положениях экрана в этом параллельном пучке.

B2  ^1.60 Расположите экран за линзой №1 и, двигая только экран, наблюдайте, как форма светового пятна на нём зависит от положения экрана. В листе ответов схематично изобразите несколько характерных фигур и запишите расстояния $d$ от линзы №1 до экрана в момент их получения.

Последовательность форм пятен при увеличении $d$ приведена на рисунке. Вместо круглых пятен могут возникать пятна, имеющие форму квадрата или ромба со скругленными углами. Изображенный на рисунке порядок фигур соответствует случаю, когда параллельный пучок падает на линзу со стороны закрепленного на ней транспортира. При освещении другой поверхности линзы на экране будут возникать картинки, отличающиеся от этих поворотом на $90^{\circ}$.

B3  ^0.30 Определите, при каком $d=d_{exp}~(d_{exp} > 10~\text{см})$ световое пятно на экране имеет одинаковые размеры $h_{exp}$ вдоль двух выделенных направлений линзы №1. Запишите величины $d_{exp}$ и $h_{exp}$ в лист ответов. Соответствующая расстоянию $d_{exp}$ форма светового пятна должна присутствовать среди фигур, изображенных вами в листе ответов для предыдущего пункта.

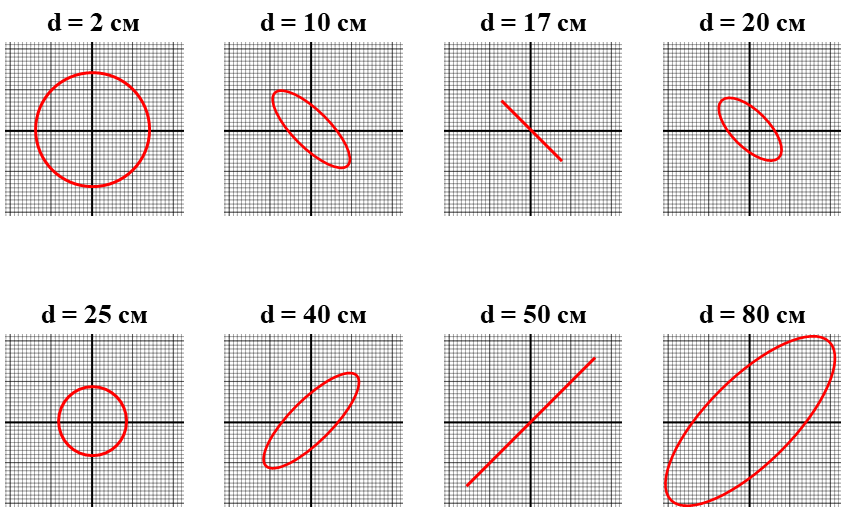
Из предыдущего пункта следует: $d_{exp} = 25~\text{см}$. Измеряем диаметр круглого пятна: $d_{exp} = 2.9~\text{см}$.

B4  ^0.80 Измерьте диаметр линзы $2R$ и запишите результат в лист ответов. Рассчитайте теоретически (с помощью геометрических построений) величину $d_{th}$, равную расстоянию между линзой №1 и экраном для получения на нём светового пятна, имеющего одинаковые размеры $h_{th}$ вдоль двух выделенных направлений линзы №1. Можете пользоваться приведенными во введении сведениями о ходе лучей, падающих на линзу в точках ее выделенных диаметров. В лист ответов запишите рассчитанные значения $d_{th}$ и $h_{th}$.

Измеряем $2R=5.5~\text{см}$. Круглое пятно получается на экране в том случае, если в его плоскости два "выделенных" узких пучка дают отрезки одинаковых длин. Два чертежа для соответствующих пучков (фокусирующихся в точках $F_{min}$ и $F_{max}$) объединены в один и представлены на рисунке.

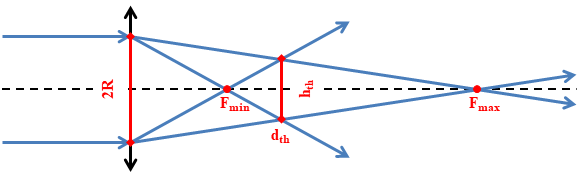
Запишем подобие двух пар треугольников (с вершинами в точках $F_{min}$, $F_{max}$ и $d_{th}$): $$\cfrac{h}{2R} = \cfrac{d-F_{min}}{F_{min}} = \cfrac{F_{max}-d}{F_{max}}$$ $$\cfrac{d}{F_{min}}-1 = 1-\cfrac{d}{F_{max}}$$ $$d = \left( D_{\text{сф}} + \cfrac{D_{\text{ц}}}{2} \right) ^{-1} = 25~\text{см}$$ $$h=2R \cdot \left( \cfrac{d}{F_{min}} - 1 \right) = 2R \cdot \left( \cfrac {\left( D_{\text{сф}} + \cfrac{D_{\text{ц}}}{2} \right) ^{-1}} {\left( D_{\text{сф}} + D_{\text{ц}} \right) ^{-1}}-1 \right) = 2R \cdot \cfrac{D_{\text{ц}}}{2D_{\text{сф}} + D_{\text{ц}}} \approx 2.8~\text{см}$$

C1  ^1.00 Расположите экран за линзой №1 и, двигая только экран, наблюдайте, как наклон освещенного отрезка на экране зависит от положения экрана. В листе ответов схематично изобразите несколько характерных картин и запишите расстояния $d$ от линзы №1 до экрана в момент их получения. На отдельном чертеже изобразите, как, по вашему мнению, будет располагаться отрезок на бесконечно удаленном экране.

Последовательность картинок, получающихся по мере увеличения $d$, приведена на рисунке. Такой порядок фигур соответствует случаю, когда параллельный пучок падает на линзу со стороны закрепленного на ней транспортира. При освещении другой поверхности линзы отрезок на экране будет поворачиваться на те же углы, но не по часовой стрелке, а против. При переходе от $d = 50~\text{см}$ к бесконечно удаленному экрану отрезок повернется еще на небольшой угол. Это можно предположить, наблюдая изображение отрезка на далекой стене аудитории.

C2  ^0.40 Измерьте два расстояния ($d_\min$ и $d_\max$), при которых направление отрезка на экране совпадает с одним или другим выделенным направлением линзы №1. Совпадают ли эти измеренные величины с определенными ранее $F_\min$ и $F_\max$?

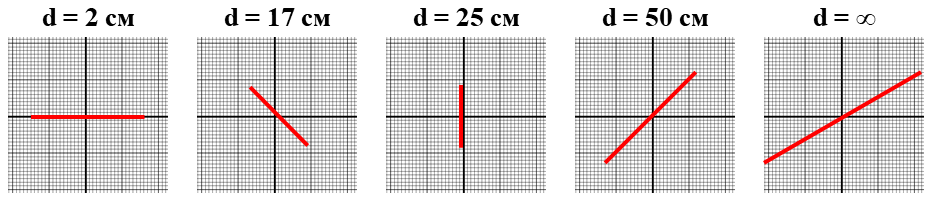
Отрезок наклонен к горизонту под углом $135^{\circ}$ (и совпадает с одним из выделенных направлений) при $d_{min} = 17~\text{см} = F_{min}$. И совпадает с другим выделенным направлением, т.е. наклонен под $45^{\circ}$, при $d_{max} = 50~\text{см} = F_{max}$.

C3  ^2.00 Для собранной вами экспериментальной установки (с параллельным пучком света, падающим на астигматическую линзу с щелевой диафрагмой) теоретически опишите наблюдаемую зависимость наклона отрезка на экране от положения экрана. Получите теоретически значение угла $\beta_{inf}$, на который повернут относительно горизонта отрезок на бесконечно удаленном экране. На какой угол $\beta_{total}$ должен поворачиваться отрезок за всё время движения экрана от $d = 0$ до $d = +\infty$ при таком взаимном расположении щели и выделенных направлений линзы, как в нашей установке?

Для описания наклона отрезка на экране, зафиксированном на некотором расстоянии $d$ от линзы, можно рассматривать только его крайнюю точку (помимо центральной, освещаемой всегда одним и тем же лучом, идущим по главной оптической оси). Распространяясь в пространстве, некоторые два "крайних" луча лежат на скрещивающихся прямых и всегда задают концы высвечиваемого на экране отрезка. На рисунке ниже эти лучи изображены красными пунктирами. Как мы знаем из пункта B2, при $d=F_{min}$ или $d=F_{max}$ все падающие на линзу лучи, в том числе ограниченные щелевой диафрагмой, должны собираться в наклонный отрезок, параллельный одному из выделенных направлений линзы. Это использовано при построении рисунка и объясняет результаты пункта C2.

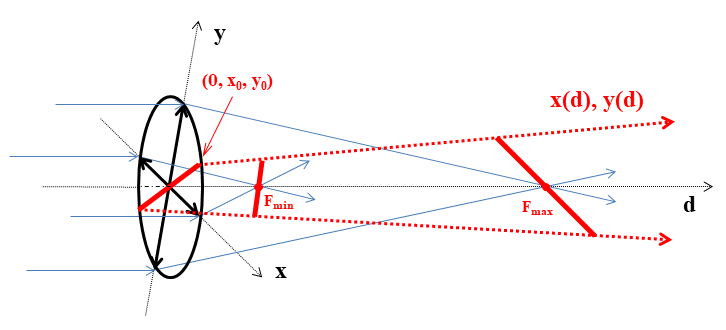
Введем систему координат с началом в центре линзы и осями $d, x, y$, причем координата $d$ будет отвечать за расстояние между линзой и плоскостью экрана, а оси $x$ и $y$ будут сонаправлены с выделенными диаметрами линзы. Пусть "крайний" луч выходит из линзы в точке $(0, x_0, y_0)$. Получим его уравнение в виде двух зависимостей: $x(d)$ и $y(d)$. Для вспомогательных выкладок ниже приведены чертежи в плоскостях $(d, x)$ и $(d, y)$.

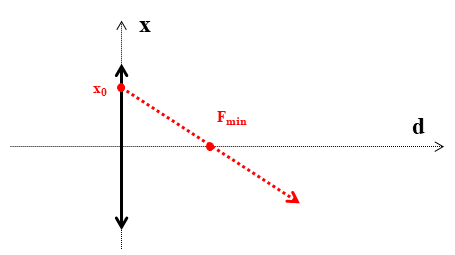
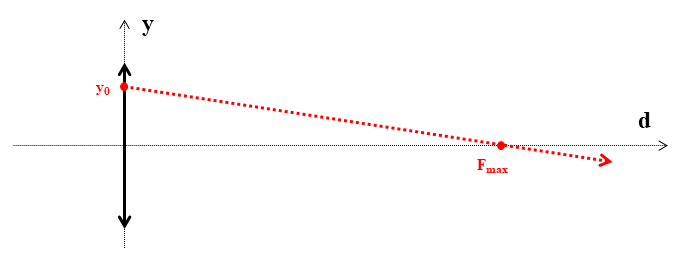
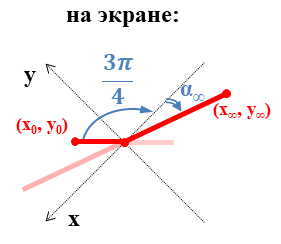
Опираясь на приведенные "плоские" рисунки, выводим уравнения, которые задают прямые в плоскостях, а в совокупности описывают "крайний" луч в пространстве: $$x = x_0 \cdot \left( 1 - \cfrac{d}{F_{min}} \right);\ y = y_0 \cdot \left( 1 - \cfrac{d}{F_{max}} \right)$$ При постепенном увеличении $d$ от $d=0$ до $d=+\infty$ сначала проходит через $0$ и становится отрицательным значение $x(d)$, а потом $y(d)$. В соответствующих точках высвеченный на экране отрезок становится параллельным выделенным направлениям линзы, что и наблюдается в эксперименте. Угол $\beta_{total}$ будем рассчитывать по рис. 7 с учетом направления вращения отрезка: $$\beta_{total} = \cfrac{3\pi}{4}+\alpha_{\infty} = \cfrac{3\pi}{4} + \arctan{\left( \lim_{d \to \infty} \cfrac{y(d)}{x(d)} \right)},$$ $$\beta_{total} = \cfrac{3\pi}{4} + \arctan{\left( \lim_{d \to \infty} \cfrac{y_0 \cdot \left( 1 - \cfrac{d}{F_{max}} \right)} {x_0 \cdot \left( 1 - \cfrac{d}{F_{min}} \right)} \right)},$$ $$\beta_{total} = \cfrac{3\pi}{4}+\arctan{\left( \cfrac{y_0}{x_0} \cdot \cfrac{F_{min}}{F_{max}} \right)}.$$ С учетом того, что щель горизонтальна, т.е. $x_0 = y_0$: $$\beta_{total} = \cfrac{3\pi}{4}+\arctan{\cfrac{F_{min}}{F_{max}}} = 2,68~рад.=154^{\circ} .$$ В качестве угла между отрезком на бесконечности и горизонтом можно взять либо этот же (тупой) угол $\beta_{total}$, либо вычислить дополнительный к нему (острый) угол $(\pi - \beta_{total})$. Таким образом, засчитывается любой из двух ответов: $$\beta_{inf}=\cfrac{3\pi}{4}+\arctan{\cfrac{F_{min}}{F_{max}}} = 2,68~рад.=154^{\circ}$$ или $$\beta_{inf}=\cfrac{\pi}{4}-\arctan{\cfrac{F_{min}}{F_{max}}} = 0,46~рад.=26^{\circ}$$.

С4  ^0.60 Докажите теоретически, что изображение отрезка - отрезок, т.е. что все промежуточные лучи после преломления приходят на экран в точках, лежащих на одной прямой с точками от крайних лучей.

В пункте C3 получено выражение для угла наклона отрезка, ограниченного "центральным" лучом и "крайним": $$\alpha(d) = \cfrac{y_0 \cdot \left( 1 - \cfrac{d}{F_{max}} \right)} {x_0 \cdot \left( 1 - \cfrac{d}{F_{min}} \right)} = \cfrac{y_0}{x_0} \cdot \cfrac{1 - \cfrac{d}{F_{max}}} {1 - \cfrac{d}{F_{min}}} .$$ При любом (не обязательно горизонтальном) направлении щели, проходящей церез центр координат, отношение $\cfrac{y_0}{x_0}$ для всех "промежуточных" точек щели одинаковое – такое же, как для "крайних". А значит выходящие из "промежуточных" точек лучи пересекают экран в точках с одинаковым $\alpha(d)$, т.е. "промежуточные" светлые точки на экране ложатся на отрезок между "крайней" точкой и "центральной". И изображение на экране является отрезком прямой линии.