
Существует дефект зрения — астигматизм — при котором хрусталик искривлён по-разному в разных направлениях, и поэтому не может сфокусировать широкий пучок лучей в одну точку. Для коррекции таких отклонений при подборе очков и контактных линз используют так называемые астигматические линзы.
Технология их изготовления сложна и обычно подразумевает, что одной из поверхностей линзы придается форма участка поверхности тора, а другая поверхность делается сферической, как при шлифовке обычных линз. Однако изучением фактической формы поверхности подобных линз мы в рамках этой задачи заниматься не будем, а сосредоточимся на исследовании действия линз на падающие на них световые пучки. С этой точки зрения тонкая астигматическая линза эквивалентна совокупности расположенных вплотную обычной сферической тонкой линзы и цилиндрической тонкой линзы. Они характеризуются своими фокусными расстояниями $F_\text{сф}$ и $F_\text{ц}$ и оптическими силами $D_\text{сф}$ и $D_\text{ц}$ соответственно.
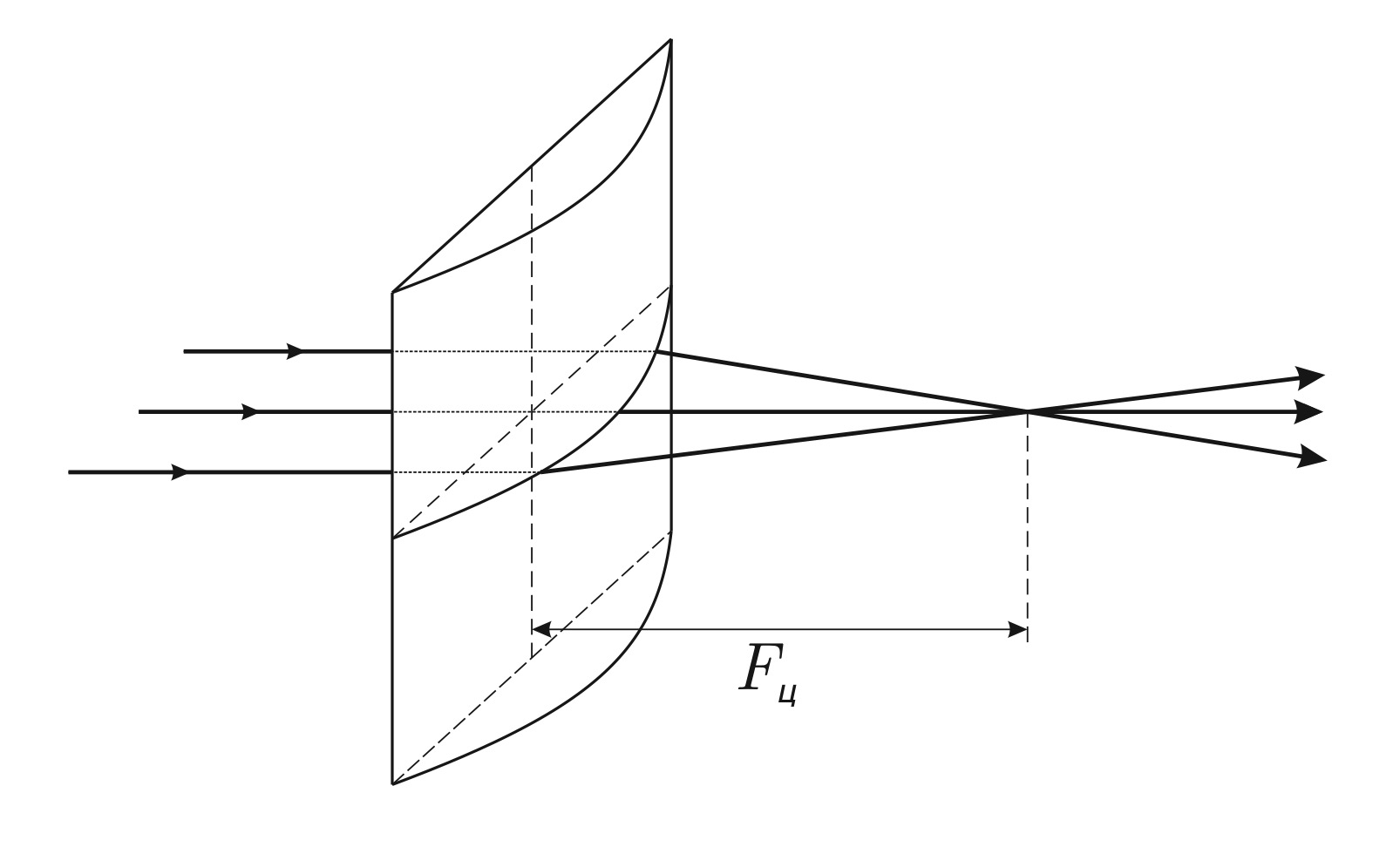
Плоскость тонкой цилиндрической линзы содержит два выделенных направления. И два соответствующих им отрезка, проходящих через центр линзы, — назовем их «выделенными диаметрами». У цилиндра отсутствует кривизна в одном из выделенных направлений, и поэтому лучи при преломлении в линзе сохраняют угол с этим направлением. Второе направление перпендикулярно первому, а узкий пучок параллельных лучей, перпендикулярных линзе и упавших в разные точки соответствующего выделенного диаметра, собирается линзой в точку на расстоянии $F_\text{ц}$ от линзы.

Три различные астигматические линзы в оправах для установки на столе
Фонарик в держателе
Картонная щелевая диафрагма (и 2 канцелярские клипсы для ее крепления к линзе?)
Картон с закрепленной на нем миллиметровкой для использования в качестве экрана
Мерная лента
Линейка
\emph{Внимание!} Не пачкайте стеклянные поверхности линз, касаясь их пальцами!
\emph{Внимание!} Запрещается наносить пометки на линзы, их оправы и закрепленные на них транспортиры.
\emph{Внимание! Изображая линзу на схеме установки, всегда отмечайте сторону, на которой укреплен транспортир!}
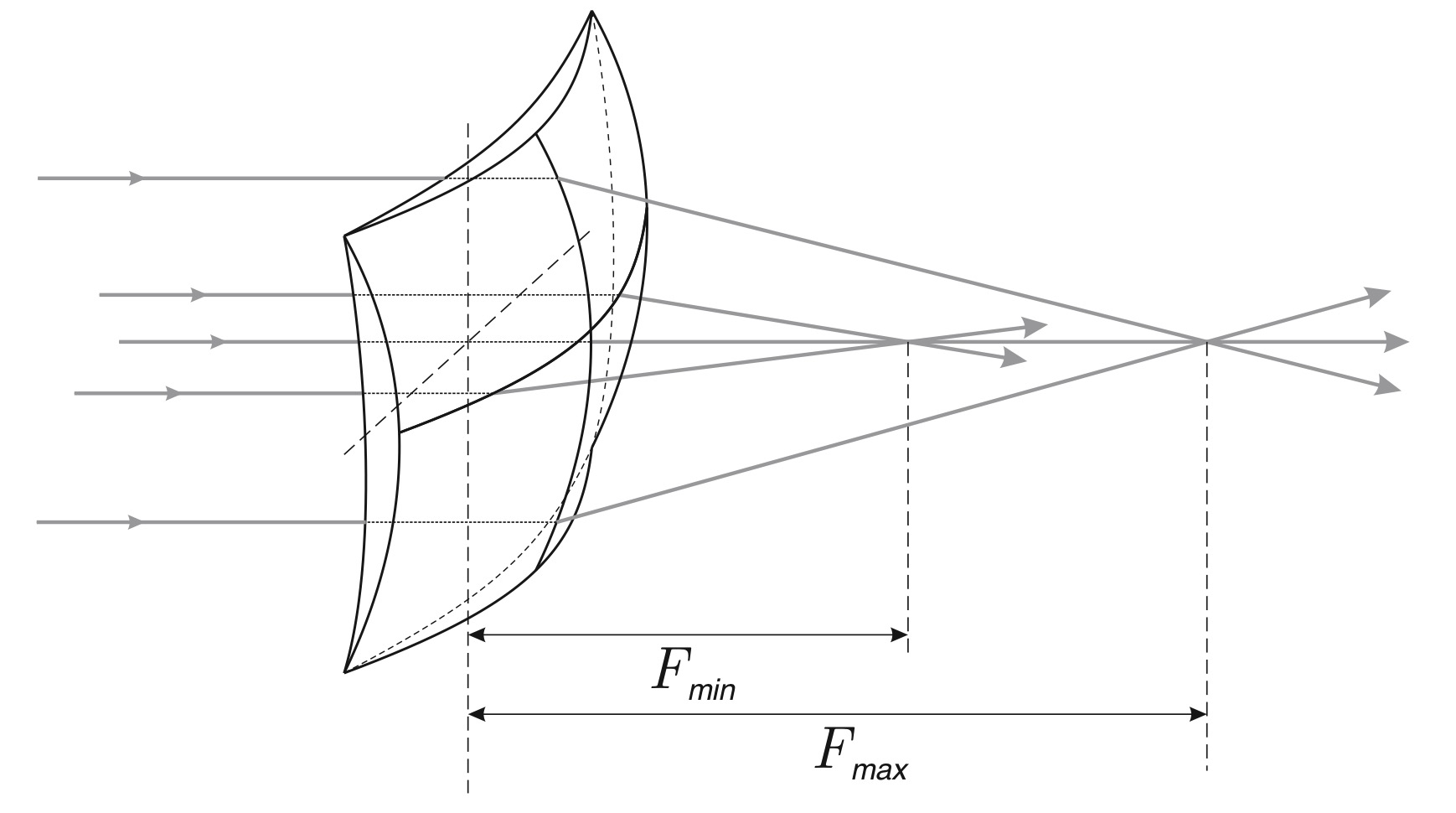
Наличие выделенных направлений у цилиндрической линзы объясняет наличие выделенных направлений у астигматической линзы. Пусть лучи одного из узких параллельных пучков упали в разные точки одного выделенного диаметра астигматической линзы, лучи другого пучка — в точки другого выделенного диаметра. Фокусные расстояния линзы для этих двух пучков лучей различаются — обозначим меньшее и большее из них как $F_\min$ и $F_\max$ соответственно.
A4
2.00
Для каждой линзы экспериментально определите фокусные расстояния для двух ее выделенных направлений: $F_\min$ и $F_\max$. В листе ответов необходимо подробно описать последовательность действий и измерений, с приведением схем использующихся установок и указанием всех применяемых элементов. Рассчитайте пары значений $D_\text{сф}$ и $D_\text{ц}$. Все полученные числа занесите в таблицу в листе ответов.
B3
0.30
Определите, при каком $d=d_{exp}~(d_{exp} > 10~\text{см})$ световое пятно на экране имеет одинаковые размеры $h_{exp}$ вдоль двух выделенных направлений линзы №1. Запишите величины $d_{exp}$ и $h_{exp}$ в лист ответов. Соответствующая расстоянию $d_{exp}$ форма светового пятна должна присутствовать среди фигур, изображенных вами в листе ответов для предыдущего пункта.
B4
0.80
Измерьте диаметр линзы $2R$ и запишите результат в лист ответов. Рассчитайте теоретически (с помощью геометрических построений) величину $d_{th}$, равную расстоянию между линзой №1 и экраном для получения на нём светового пятна, имеющего одинаковые размеры $h_{th}$ вдоль двух выделенных направлений линзы №1. Можете пользоваться приведенными во введении сведениями о ходе лучей, падающих на линзу в точках ее выделенных диаметров. В лист ответов запишите рассчитанные значения $d_{th}$ и $h_{th}$.
В этом пункте, как и в предыдущем, требуется освещать линзу №1 параллельным световым пучком кругового поперечного сечения. Вставьте в оправу линзы №1 картонную щелевую диафрагму, задействуя свободные от линзы бороздки ее оправы. Щель должна располагаться горизонтально. Поверните линзу так, чтобы ее сторона с диафрагмой была обращена к источнику.
emph{Внимание!} Новые диафрагмы выдаваться не будут!
C1
1.00
Расположите экран за линзой №1 и, двигая только экран, наблюдайте, как наклон освещенного отрезка на экране зависит от положения экрана. В листе ответов схематично изобразите несколько характерных картин и запишите расстояния $d$ от линзы №1 до экрана в момент их получения. На отдельном чертеже изобразите, как, по вашему мнению, будет располагаться отрезок на бесконечно удаленном экране.
C3
2.00
Для собранной вами экспериментальной установки (с параллельным пучком света, падающим на астигматическую линзу с щелевой диафрагмой) теоретически опишите наблюдаемую зависимость наклона отрезка на экране от положения экрана. Получите теоретически значение угла $\beta_{inf}$, на который повернут относительно горизонта отрезок на бесконечно удаленном экране. На какой угол $\beta_{total}$ должен поворачиваться отрезок за всё время движения экрана от $d = 0$ до $d = +\infty$ при таком взаимном расположении щели и выделенных направлений линзы, как в нашей установке?