Как известно, при дифракции на отверстии лучи приближённо расходятся на $\theta = \frac{\lambda}{2R_0}$. Тогда размер пятна на экране $$R \approx R_0 + L \theta = R_0 \left(1 + \frac{L \lambda}{2R_0^2} \right)$$

Из ЗСЭ получим $I_0 \pi R_0^2 \approx I \pi R^2$. Тогда ответ $$I = I_0 \frac{1}{ \left(1 + \frac{L \lambda}{2R_0^2} \right)^2}$$

Продифференцировав выражение для размера пятна, получим, что $R_{\text{min}}$ соответствует $R_0 = \sqrt{L \lambda /2} $. Тогда ответ
$$R_{\text{min}} \approx \sqrt{2 L\lambda}$$

Лучи расходятся на угол $\theta$. Расстояние до фокуса $F$. Тогда диаметр пятна $$D_F \approx 2 \theta F = 2 \frac{F\lambda}{D}.$$

Здесь считаем, что радиус первого светлого пятна определяется первым минимумом. Можно считать, что радиус первого светлого пятна в два раза меньше, чем первый минимум.

Запишем ЗСЭ:
$$I_0 \frac{\pi}{4}D^2 = I \pi R^2 = I \pi \left(\frac{F\lambda}{D}\right)^2.$$
Тогда ответ:
$$I \approx I_0 \frac{D^4}{4 F^2 \lambda^2}$$

Точный ответ можно посчитать при помощи зон Френеля. Пусть интенсивности $I$ и $I_0$ соответствуют амплитудам $E$ и $E_0$ соответственно. Заметим, что фокус -- такая точка, что лучи проходят одинаковые пути от внешней поверности линзы до него и, соответственно, прибывают туда в фазе. Если бы линзы не было, то из отверстия из-под линзы в фокусе было бы видно $m$ зон Френеля, $\frac{1}{4}D^2 = m \lambda F$. Тогда длина спирали Френеля равна $\pi m E_0 = \frac{\pi}{4}\frac{D^2}{\lambda F} E_0$. Заметим, что когда есть линза, все волновые фронты приходят в фокус в фазе и спираль "выпрямляется". Тогда $E = E_0 \frac{\pi}{4} \frac{D^2}{\lambda F}$ и ответ:
$$I = I_0 \frac{\pi^2}{16}\frac{D^4}{F^2 \lambda^2}$$
Видно, что оценка в предыдущем пункте сходится с ответом.\\
Можно получить ответ, если показать, что при некой ширине ког в фокусе линзы будет наблюдаться большая интенсивность, чем на поверхности источника.

Уравнения параболы , при вращении которой образуется зеркало $ y^2 = 2px$. Как известно, парабола -- ГМТ точек, равноудалённых от некой прямой и точки. Пусть фокусное расстояние $F$. Тогда расстояние от точки $(0, 0)$ до прямой тоже $F$. Рассмотрим точку параболы, $x$ - координата которой равна координате фокуса. Тогда она удалена на $2F$ от прямой и от фокуса. Получаем, что $4F^2 = 2 pF$ и ответ: $$F = \frac{1}{2}p$$.

Опять запишем ЗСЭ. Оценка углового расхождения аналогична $\theta \approx \frac{\lambda}{D}$. Тогда размер пятна в фокусе $R = F \theta = \frac{F \lambda}{D} = \frac{p \lambda}{D}$. Из ЗСЭ получаем:
$$I \approx I_0 \frac{D^4}{p^2 \lambda^2}$$

То есть, $I \sim \lambda^{-2}$. Тогда при уменьшении длины волны волны в два раза интенсивность увеличивается в 4 раза.

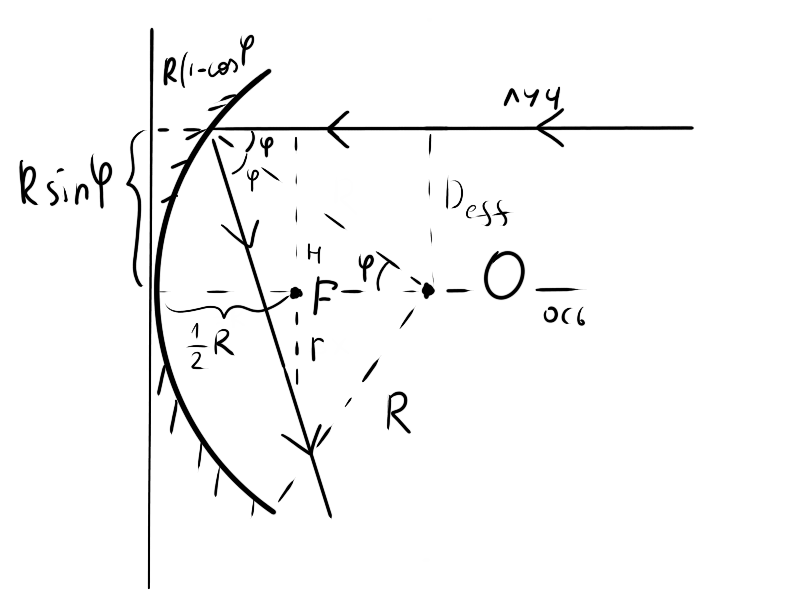
Посчитаем фокусное расстояние. Из чертежа ниже видно, что оно равно $\frac{1}{2} R$

Первый эффект: дифракционное размытие. Тогда радиус пятна
$r_D = \frac{\lambda R}{2D}$.

Второй эффект: аберрация. Из чертежа видно, что
\begin{align*}
H =&\; R \sin \varphi \\
H + r =&\; R \tan{2\varphi} \left(\frac{1}{2} - (1 - \cos \varphi)\right)\\
r =&\; R \tan{2\varphi} \left(\cos \varphi - \frac{1}{2}\right) - R \sin \varphi \\
r_A \approx&\; \frac{1}{2} \varphi^{3} R = \frac{1}{2} (D/R)^3 R = \frac{D^3}{2R^2}.\\
\end{align*}

Для $D_1$ реализуется дифракция. Для $D_2$ аберрация. Надо посчитать.

Для дифракции считаем как раньше через энергию:
$$I \left( \frac{\lambda R}{2D} \right)^2 = I_0 \frac{D^2}{4} ,$$
$$I = I_0 \frac{D^4}{\lambda^2 R^2} .$$
Для аберрации посчитаем интенсивность в центре как отношение мощности к радиусу. Возъмём в центре диск радуса $r$, в этот диск попадают лучи из зеркала диаметром
$$d = (2 r R^2)^{1/3}$$.
Мощность, которая собирается этим зеркалом $I_0 \pi d^2/ 4$. Интенсивность в этом диске вокруг центра:
$$I = \frac{I_0 \pi (2 r R^2)^{2/3}}{4 \pi r^2} = I_0 \frac{2^{2/3}R^{4/3}}{4r^{4/3}}.$$
Видно, что в предельном переходе ответ стремится к бесконечности.

Дифракция:
$$ I \approx \frac{D^4}{\lambda^2} I_0$$

Второй случай: никто не знает. Но Зенькович говорит вот так:
Здесь же в фокус, точнее, в ту область, в которой дифрация усредняет интенсивности попадают только те лучи, которые падали под $\varphi < \varphi_{crit}$, где$\varphi_{crit}$ -- угол, при котором смещение, вызванное аберрацией, меньше, чем дифракционное отклонение: $$\frac{1}{2}\varphi_{crit}^3 R = \frac{1}{2}R \frac{\lambda}{D}$$
$$\varphi_{crit} \approx \left(\frac{\lambda}{D}\right)^{\frac{1}{3}}$$
Площадь, лучи из которой упадут на зеркало под углом, меньшим $\varphi_{crit}$, равна $\pi R^2 \varphi_{crit}^2$
Тогда запишем ЗСЭ:
$$I_0 \pi R^2 \varphi_{crit}^2 = I \frac{1}{4} \pi R^2 \frac{\lambda^2}{D^2}$$
$$I \approx I_0 \left(\frac{\lambda}{D}\right)^{-\frac{4}{3}}$$
Тогда при уменьшении длины волны интенсивность увеличится в $2^\frac{4}{3} \approx 2.5$ раз. Это ответ на второй вопрос.

Амплитуда падающей волны $E_S=√(I_S )$. В нулевой максимум попадают все волны, которые пропускаются щелью, причём с одинаковой фазой. Поэтому, амплитуда нулевого максимума
$$E_0=a/d E_S,$$
интенсивность нулевого максимума
$$I_0=(a/d)^2 I_S.$$

Направление на максимум $h$:

$$\sin⁡φ=hλ/d.$$

Находим амплитуду максимума с номером $h$:

$$E_h=\frac{E_0}{a} ∫_0^a e^{(-i 2π/λ x \sin⁡φ )} dx=\frac{E_0}{a} ∫_0^a e^{(-i 2π x/d h)} dx ∼ E_S \frac{\sin⁡(πha/d)}{πh}.$$

Тут опущена фаза, которая не важна для интенсивности. В итоге:

$$I_h=E_h^2=I_S \left( \frac{ \sin⁡(πh a/d)}{ πh} \right)^2.$$

Плоская волна в плоскости решетки является источником вторичных волн. То есть непропускающая часть $d-a$ поглощает не только энергию, которая идёт в нулевой максимум, но и всё то, что рассеивалось бы во все направления. Можно показать, что дополняющая решетка рассеивает туда же и столько же, сколько и начальная.
Поглощает в нулевом направлении:

$$I_0=((d-a)/d)^2 I_S,$$

Поглощает во всех направлениях (и столько же попадает в реальные максимумы):

$$βI_S.$$

Итого:

$$1=(a/d)^2+((d-a)/d)^2+2β$$

$$β=\frac{a(d-a)}{d^2} $$

Поглощается решеткой:

$$γ=((d-a)/d)^2+β=(d-a)/d.$$

Если что, суммарно на экран попадает доля энергии

$$(a/d)^2+β=a/d,$$

Что равно $1-γ$, как и должно быть из ЗСЭ.