A1  ^0.50 Покажите, что суммарная сила, действующая на кольцо, определяется выражением: $$ \vec F_{tot} = - \mu mg \cdot f \left( \frac{v(t)}{\omega (t)\ r} \right) \hat x, $$ где $$ f(a) = \frac{1}{2 \pi} \int \limits_0^{2 \pi} \frac{a - \sin \theta}{\sqrt{ 1 + a^2 - 2 a \sin \theta}} d \theta $$

Обозначим скорость кусочка, видимого из центра кольца под углом $d \theta$ как $\vec{u}$. Так как тело движется, а коэффициент трения не зависит от направления движения, то сила трения, действующая на выбранный кусочек, направлена противоположно его скорости. Тогда её можно записать в таком виде: $$ d \vec{F}_{fric} = - \frac{\vec{u}}{u} \mu \: dN = - \frac{(v-\omega r \sin \theta) \hat x + (\omega r \cos \theta) \hat y}{\sqrt{v^2 + (\omega r)^2 - 2 v \omega r \sin \theta}} \mu mg \: \frac{d \theta}{2 \pi} $$ Полная сила трения получается при интегрировании выражения вдоль всего кольца, т. е. в диапазоне углов от $0$ до $2 \pi$. Несложно заменить, что $F_{tot \: y} = 0$, так как всё выражение меняет знак при замене $\theta \rightarrow \pi - \theta$. Физически это соответствует тому, что силы, действующие на кусочки, симметричные относительно оси OX, проходящей через центр кольца, компенсируют y-составляющие друг друга. Разделив числитель и знаменатель на $\omega r$, приходим к искомому выражению.

A2  ^0.50 Покажите, что суммарный момент, действующий на кольцо, равен: $$ \tau_{tot} = - \mu mg r f \left(\frac{\omega(t) r}{v(t)} \right) $$

$$ d \vec{\tau} = \left[ \vec r \times d \vec{F}_{fric} \right] = - \frac{\left[\vec r \times \vec u \right]}{u} \mu g \: dm $$ В векторное произведение входит только компонента $\vec u$, перпендикулярная радиусу, т. е. $u_\tau = \omega r - v \sin \theta$. подставляя всё в итоговое выражение, получим: $$ \vec \tau = - \mu m g r\int \limits_0^{2 \pi} \frac{\omega r-v \sin \theta }{\sqrt{v^2 + (\omega r)^2 - 2 v \omega r \sin \theta}} \: \frac{d \theta}{2 \pi}, $$ откуда после сокращения на $v$ получится искомая формула.

A3  ^0.10 Докажите, что уравнения движения имеют вид: $$ \dot v = - \mu g\cdot f \left( \frac{v}{\omega r} \right) \\ \dot \omega r = - \mu g \cdot f \left( \frac{ \omega r}{v} \right) $$

Векторная сумма сил всегда сонаправлена скорости, поэтому $| \dot{\vec{v}} | = \dot{|v|} $, то есть тангенциальное ускорение равно нулю. Тогда уравнения движения примут вид: $$ m \dot v = - \mu mg f \left( \frac{v}{\omega r} \right) \\ m \dot \omega r^2 = - \mu m g r f \left( \frac{\omega r}{v} \right), $$ откуда после сокращения на $m$ и $mr$ соответственно получатся искомые равенства.

B1  ^0.50 Докажите: a) $ f(0) = 0, \: f(1) = \dfrac{2}{\pi}, \: f(\infty) = 1$ b) $ f(a) $ строго возрастает при $a \geqslant 0 $

a) $$ f(0) = \frac{1}{2 \pi} \int \limits_0^{2 \pi} -\sin \theta \: d \theta = 0 \\ f(1) = \frac{1}{2 \pi} \int \limits_0^{2 \pi} \frac{1-\sin \theta}{\sqrt{2 - 2 \sin \theta}} \: d \theta = \frac{1}{2 \pi}\int \limits_0^{2 \pi} \sqrt{\frac{1-\sin \theta}{2}} \: d \theta = \\ = \frac{1}{2 \pi}\int \limits_0^{2 \pi} \left|\sin \left(\frac{\theta}{2} - \frac{\pi}{4} \right) \right| d \theta = \frac{1}{\pi}\int \limits_0^{\pi} \sin \left( \frac{\theta}{2} \right) \: d \left( \frac{\theta}{2} \right) = \frac{2}{\pi} \\ f(\infty) = \frac{1}{2 \pi} \int \limits_0^{2 \pi} \lim \limits_{a \rightarrow \infty} \frac{a - \sin \theta}{\sqrt{1 +a^2 - 2a \sin \theta}} \: d \theta = \frac{1}{2 \pi} \int \limits_0^{2 \pi} d \theta = 1 $$

b) $$ \frac{df}{da} = \frac{1}{2 \pi} \int \limits_0^{2 \pi} \frac{\partial}{\partial a} \left[ \frac{a - \sin \theta}{\sqrt{1 +a^2 - 2a \sin \theta}} \right] \: d \theta = \\ = \frac{1}{2 \pi} \int \limits_0^{2 \pi} \left[ \frac{1}{\sqrt{1 +a^2 - 2a \sin \theta}} - \frac{(a - \sin \theta)^2}{(1 +a^2 - 2a \sin \theta)^{3/2}} \right] \: d \theta = \\ = \frac{1}{2 \pi} \int \limits_0^{2 \pi} \frac{cos^2 \theta}{(1 +a^2 - 2a \sin \theta)^{3/2}} \: d \theta > 0 $$

B2  ^0.30 Рассмотрим поведение параметра $a(t) = \dfrac{v(t)}{\omega (t) r} $. Покажите, что происходит с $a(t)$ (растёт/уменьшается/остаётся неизменным) в каждом из следующих случаев: a) в некоторый момент $a(t) = 1$ b) в некоторый момент $a(t) < 1$ c) в некоторый момент $a(t) > 1$

$$ \dot a = \frac{d}{dt} \left( \frac{v}{\omega r}\right) = \frac{\dot v \: \omega r- v \: \dot \omega r}{(\omega r)^2} = - \frac{\mu m g}{\omega r} \bigg( f(a) - a f \left(\tfrac{1}{a} \right) \bigg) $$ Анализируя данное выражение, получаем: $$ f(a) - a f \left(\tfrac{1}{a} \right) = \frac{1}{2 \pi} \int \limits_0^{2 \pi} \frac{a - \sin \theta - a( 1- a \sin \theta)}{\sqrt{1 +a^2 - 2a \sin \theta}} d \theta= \\ \\ = \frac{a^2-1}{2 \pi} \int \limits_0^{2 \pi} \frac{\sin \theta}{\sqrt{1 +a^2 - 2a \sin \theta}} d\theta $$ В области отрицательных значений подынтегральной функции знаменатель больше, чем в области положительных, поэтому интеграл всегда положителен. Таким образом: $$ sign( \dot a) = sign(1 - a); \\ \dot a=0 \Rightarrow a =1. $$ Заметим, что ответ можно было бы получить и из более простых логических соображений

B3  ^0.60 Нарисуйте качественно на графике, осями которого являются $v$ и $\omega r$, траектории, отображающие разное движение кольца, то есть при заданных $v_0$ и $\omega_0 r$ нарисуйте, как они будут изменяться с течением времени. Необходимо нарисовать хотя бы одну траекторию на каждый пункт предыдущего задания. Кроме того, нарисуйте траекторию, проходящую через точку $(v_0, 0)$ и еще одну, начинающуюся в точке $(0, \omega_0 r)$ Подпишите оси графика и укажите направления движения системы для каждой нарисованной траектории

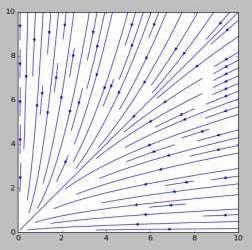
Как можно было заметить из предыдущего пункта, все траектории асимптотически стремятся к единице. При этом, $\dot v < 0$ и $\dot \omega r <0$. Приведём искомый график:

B4  ^0.10 Вычислите мгновенную мощность, которая расходуется, когда есть только угловая скорость $\omega$ $(v = 0)$, и отдельно, когда присутствует только линейная $v$ $(\omega = 0)$.

В случае отсутствия вращательного движения сила трения, действующая на каждый кусочек, направлена против оси X. Тогда: $$ P_v = - F_{tot} v = - \mu mg \: v $$ В случае отсутствия поступательного движения $$ P_\omega = - \tau_{tot} \omega = - \mu mg \: \omega r $$ Более строгие рассуждения будут приведены в пункте B5.

B5  ^0.60 Для заданных $v$ и $\omega$ вычислите мгновенную мощность $P$, которая расходуется на трение в данный момент времени. Дайте ответ в виде интеграла с безразмерной переменной.

$$ P = \int \vec u \: \cdot \: d \vec F_{fric} = - \mu mg \: \int \limits_0^{2 \pi} \vec{u} \: \cdot \: \frac{\vec u}{u} \:\frac{d \theta }{2 \pi} = - \mu mg \: \omega r \int \limits_0^{2 \pi} \frac{u}{\omega r} \:\frac{d \theta }{2 \pi} $$ Подставляя выражение для скорости кусочка $\vec u$:

B6  ^1.20 Предположим, что кольцу придали определённую начальную кинетическую энергию $E_0$. Каково должно быть соотношение $a_0 = \dfrac{v_0}{\omega_0 r}$, при котором кольцо будет двигаться максимальное время? Подсказка: Постарайтесь дать ответ на предыдущий пункт при помощи только $E_0$ и $a_0$ (и других данных из этого пункта), исключив из уравнения $v$ и $\omega$

Воспользуемся подсказкой :) $$ E = \frac{m}{2} \Big[ v^2 + (\omega r)^2 \Big] = \frac{m}{2} (\omega r)^2 \:( a^2 + 1) \\ m \: \omega r = \sqrt{2 mE} \: \cdot \: \frac{1}{\sqrt{1 + a^2}} \\ P(a, E) = - \mu g \sqrt{2 mE} \; \cdot \int \limits_0^{2 \pi} \sqrt{1 - \frac{2a}{1 + a^2} \sin (\theta)} \: \: \frac{d \theta }{2 \pi} $$ Анализировать последнее выражение можно несколькими способами. Например, взяв частную производную по a $$ \frac{\partial}{\partial a} \Big( P(a, E) \Big) = \mu g \sqrt{2 mE}\; \: \frac{1 - a^2}{1+a^2} \; \cdot \int \limits_0^{2 \pi} \frac{\sin \theta}{\sqrt{1 +a^2 - 2a \sin \theta}} \frac{d\theta}{2 \pi} $$ где интеграл в правой части совпадает с интегралом в $B2$ и имеет положительные значения при любых $a$. Так как при $a<1$ функция $P\:$ убывает, а при $a>1 - $ возрастает, то её минимум реализуется в $a_0=1$. Из того факта, что мощность $P$ всегда отрицательна и стремится к $P \rightarrow 0$ только при $E \rightarrow 0$ очевидно, что движение может закончиться только при $E = 0$. Также, следует заметить, что движение с параметром $a = 1$ устойчиво, а значит, при $a_0 = 1$ всё движение будет происходит с минимально возможной мощностью, т. е. пройдет максимально возможное время при заданной начальной энергии $E = E_0$

B7  ^0.50 Каково максимальное время движения при начальной энергии $E_0$?

Как мы выяснили в предыдущем пункте, движение, продолжающееся максимальное время происходит при $a= 1$. Тогда время можно найти из уравнения: $$ \dot E = P(1, E) = - \mu g \sqrt{2 mE} \; \cdot \int \limits_0^{2 \pi} \sqrt{1 - \sin (\theta)} \: \: \frac{d \theta }{2 \pi} $$ Интеграл вычисляется аналогично пункту $B1$ с помощью тригонометрической замены, указанной в условии. $$ \int \limits_0^{2 \pi} \sqrt{1 - \sin (\theta)} \: \: \frac{d \theta }{2 \pi} = \frac{\sqrt 2}{\pi} \int \limits_0^\pi \sin \left( \frac{\theta}{2} \right) d \left( \frac{\theta}{2} \right) = \frac{2 \sqrt{2}}{\pi} $$ Разделяя переменные, получим $$ \int \limits_{E_0}^0 \frac{dE}{\sqrt{E}} = - \mu g \sqrt{m} \cdot \frac{4}{\pi} \int \limits_{0}^\tau dt $$ Из чего несложно выразить ответ.

C1  ^0.60 Напишите заново уравнения движения из пункта А3 таким образом, чтобы они подходили под новое условие.

Вывод уравнения для величины силы трения и момента силы трения остаётся тем же, однако, теперь полная реакция опоры равна $N = mg \cos \alpha$. Таким образом, суммарный момент, действующий на кольцо, просто умножится на $\cos \alpha$. С уравнениями для проекций сил, лежащих в плоскости движения немного сложнее: суммарная сила теперь не сонаправлена со скоростью кольца. Обозначив $\cos \varphi = (\widehat{\vec v , \: \vec g_{\tau}})$, где $\vec g_\tau \: -$ составляющая вектора $\vec g$, лежащая вдоль плоскости, получим уравнения:

C2  ^2.00 При заданных начальных $\omega_0$ и $v_0 = 0$ нарисуйте все возможные семейства траекторий движения кольца в координатах $(v, \omega r)$ (для каждого типа кривых нарисуйте свой график). Укажите следующие составляющие: a) cоответствующие значения параметров; b) конечные точки (в которые траектории приходят за конечное или бесконечное время) в плоскости $(v, \omega r)$ . Здесь достаточно написать для каждой составляющей, что она стремится к нулю/ стремится к бесконечности/ равна или стремится к какой-то положительной величине. Подпишите оси графика и укажите направления движения системы для каждой нарисованной траектории

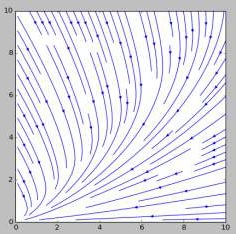
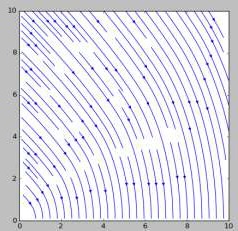
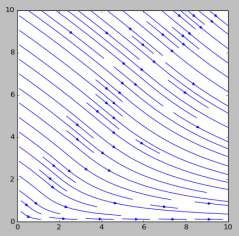
Так как при начале движения кольцо имеет нулевую скорость $v_0 = 0$, то в предыдущем уравнении на протяжении всего движения $\cos \varphi = 0$. $\dot \omega < 0$, т.е. $\omega \rightarrow 0 $. В зависимости от величины $\tan \alpha$ возможны различные случаи: $v \rightarrow 0$, $v \rightarrow const \:$ и $v \rightarrow \infty \:$. Выбор одного из этих случаев определяется знаком $\dot v$ при $\dfrac{v}{\omega r} \rightarrow \infty$. Искомые траектории приведены на рисунках.