Когда мы толкаем наполовину пустую бутылку с водой по плоскости, колебания жидкости внутри нее вызывают резкое дерганное движение системы. В данной задаче мы изучим данный процесс и построим теорию, объясняющую данное явление. Для первичного ознакомления приведем результаты эксперимента, в котором мы толкнем бутылку с водой, и посмотрим, как зависит ее положение от времени. Во всех экспериментах в течение задачи будет использоваться одна и таже бутылка, поэтому ее параметры данные в одной части можно использовать в другой.

Часть А. Кинематика воды в бутылке

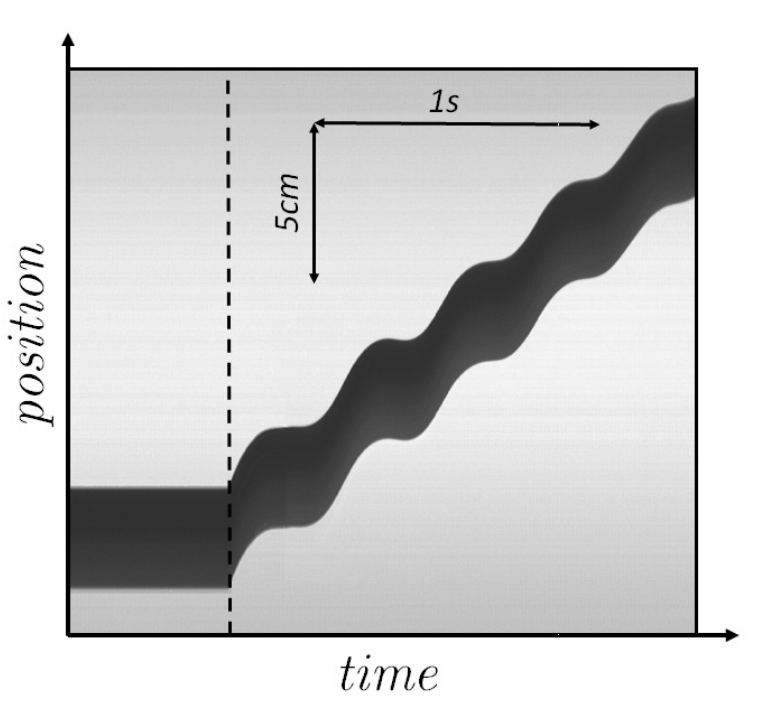
В первую очередь рассмотрим, как вода бултыхается внутри цилиндрического сосуда. Для экспериментального изучечния закрепим бутылку радиуса $R=5.0~\text{см}$ на горизотальной оси и путем небольших поступательных колебаний оси создадим колебания уровня воды, а затем подождем, пока система не перейдет в некоторое достаточно устойчивое стационарное состояние колебаний жидкости внутри сосуда.

Чтобы измерить скорость потока жидкости, наполним ее полистроловыми шариками (плотность $1.06~\text{г}/\text{см}^3$, диаметр $0.7~\text{мм}$) и сфотографируем стационарное состояние системы камерой с выдержкой (выдержка — интервал времени, в течение которого свет попадает на участок светочувствительного материала или светочувствительной матрицы) $T_\text{e}=1/10~\text{с}$, это время меньше полупериода колебаний воды в сосуде.

Момент импульса воды относительно оси бутылки связан с угловой скоростью поворота плоскости воды $\dot{\theta}$ и характеристиками системы через некоторый безразмерный коэффициент $\alpha$:

\[ L_\text{w} = \alpha \cdot \pi \rho R^4 L \dot{\theta}, \]
где $\rho$ — плотность воды, $R$ — радиус бутылки, $L$ — ее длина.

A1  ^0.20 Чему равно теоретическое значение $\alpha_\text{solid}$, если заменить воду на твердое тело постоянной плотности совпадающей с плотностью воды?

A2  ^4.50 Определите коэффициент $\alpha$ в проведенном эксперименте. Точки, в которой Вы измеряете скорость задавайте парой чисел в полярных координат с центром в оси бутылки $r, \varphi$.

A3  ^0.50 Постройте график характеризующий Ваши измерения в координатах $r/R$ vs $\varphi/\pi$.

A4  ^0.20 Сравните полученный $\alpha$ с теоретической оценкой:
\[ \alpha_\text{theory} = \frac{4}{\pi^2} - \frac{1}{4}, \]
полученной в XIX веке лордом Рэлейем.

Теперь будем измерять, как угол $\theta$ зависит от времени при стационарных колебаниях. Далее применим преобразование Фурье к полученой зависимости $\theta(t)$, т.е. получим спектральную характеристику свободных колебаний жидкости внутри бутылки. Расстояние от центра масс полуцилиндра до его оси обозначьте за $a$.

A5  ^0.30 По данным представленным на риснуке оцените собтсвенную частоту колебаний системы $\omega_0$ и ее добротность $1/\zeta$.

A6  ^0.70 Оцените $\alpha$ из спектральной характеристики колебаний.

Часть B. Динамика системы

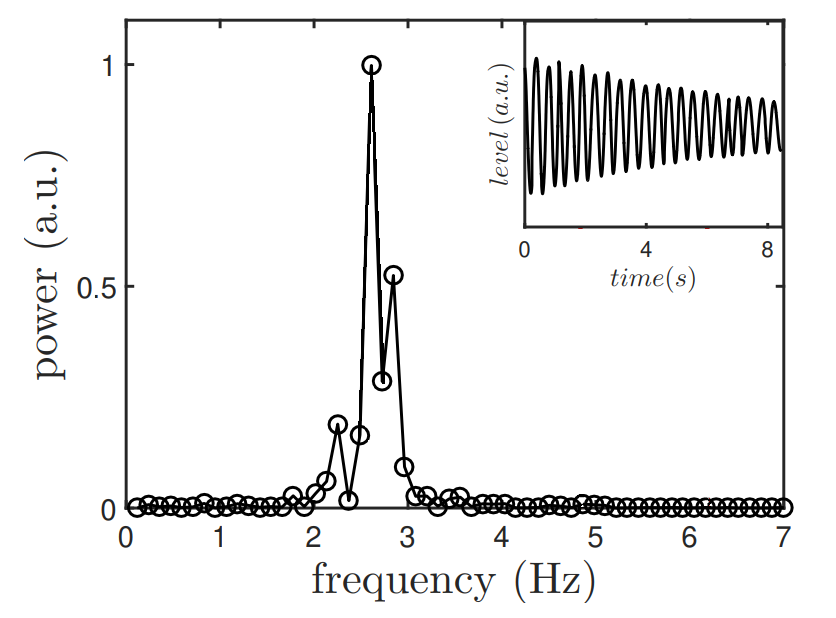
В прошлой части мы пришли к тому, что колебания воды в бутылки с допустимой точностью можно аппроксимировать колебаниями твердого тела полуцилиндрической формы с моментом инерции $I_0 = \alpha \cdot \pi \rho R^4 L$ и массой $m=\dfrac{\pi}{2} \rho R^2 L$ вокруг его оси. Таким образом бутылку с водой можно представить, как систему из колец суммарной массы $M$ и соосного им полуцилиндра. Причем кольца массы $M$ катятся без проскальзывания по плоскости, а полуцилиндр подвешен за ось колец и не взаимодействует с плоскостью.

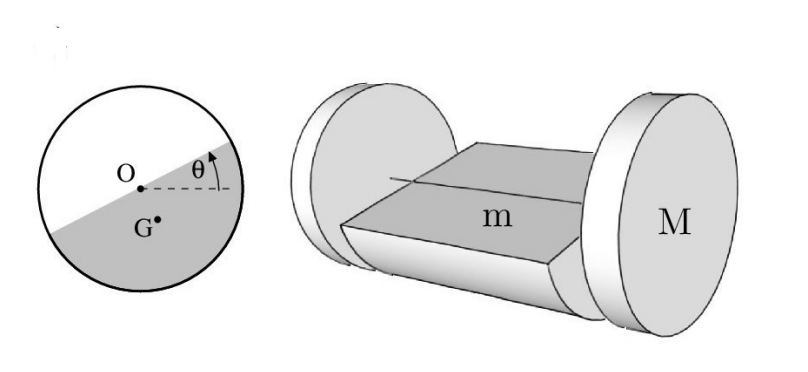
Вся система может двигаться вдоль горизонтальной оси $x$ перпендикулярной оси вращения системы. Параметрами нашей системы будет пара переменных $x$ и $\theta$, поэтому все уравнения в ответах пишите в терминах этих переменных и их производных по времени, например $\ddot{x}$.

B1  ^0.30 Запишите II закон Ньютона для всей системы системы и уравнение вращательного движения для колец.

B2  ^0.20 Получите из уравнений предыдущего пункта уравнение, в котором есть только константы, параметры нашей системы и их производные.

B3  ^0.30 Запишите уравнение динамики вращательного движения для полуцилиндра, как дифференциальное уравнение второго порядка.

B4  ^0.50 Найдите угловую частоту колебаний системы $\Omega$. Запишите решений полученной системы из двух уравнений, которое описывает то, как бутыка катиться рывками по плоскости.

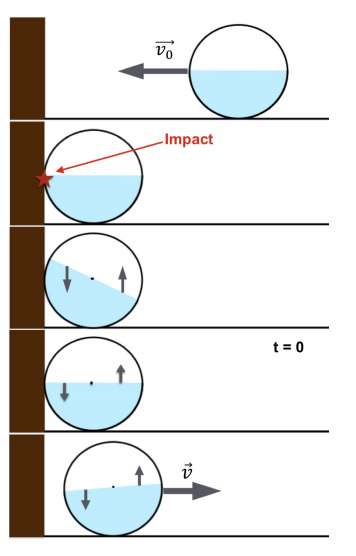
Для подтверждения данной теории проведем следующий эксперимент. Разгоним поступательно систему до скорости $v_0$ и столкнем ее со стенкой. В нашем случае масса воды $m=2.780~\text{кг}$, $M=0.910~\text{кг}$, $L=70~\text{см}$.

Так как масса воды в несколько раз больше массы бутылки, будем считать, что $\eta$ кинетической энергии перед ударом переходит в энергию колебаний, а остальная рассеивается. Ниже представлена схема, как это происходит.

B5  ^0.30 Пусть амплитуда колебаний скорости бутылки $\gamma v_0$ после отскока от стенки. Выразите $\gamma$ через известные велечины и $\eta$.

Далее приведены результаты измерения $\dot{x}/v_0$ vs $t$.

B6  ^1.50 Постройте график $\dot{x}/v_0$ vs $t$.

B7  ^0.20 Найдите экспериментальное значение $\Omega$, сравните его с теоретически.

B8  ^0.30 Найдите значение $\eta$.