A1  ^0.20 Чему равно теоретическое значение $\alpha_\text{solid}$, если заменить воду на твердое тело постоянной плотности совпадающей с плотностью воды?

\[ \alpha = \frac{1}{4} \]
$1/2$ от того, что только половина бутылки заполнена и $1/2$ от того, что тело равномерной плотности.

A2  ^4.50 Определите коэффициент $\alpha$ в проведенном эксперименте. Точки, в которой Вы измеряете скорость задавайте парой чисел в полярных координат с центром в оси бутылки $r, \varphi$.

\[ L = I \dot{\theta} = \int \int \rho H r^2 v_\tau \cdot dr \cdot d\varphi = \int \int \rho H R^3 \frac{r^3}{R^3} \dot{\theta} \frac{v_\tau}{v_0} \cdot dr \cdot d\varphi, \]
где $r$ — растояние от центра бутылки до трека, $\varphi$ — угол между горизонаталью и радиус-вектором начала трека, $R$ — радиус бутылки, $v_\tau$ — тангенциальная составляющая скорости жидкости, $v_0$ — скорость поверхности жидкости около края бутылки.

Тогда
\[ L = \pi \rho L R^2 \dot{\theta} \int \int \frac{r^3}{R^3} \frac{v_\tau}{v_0} \cdot d\frac{r}{R} \cdot d\frac{\varphi}{\pi} \]

Таким образом:

\[ \alpha = \left\langle \frac{r^3}{R^3} \cdot \frac{v_\tau}{v_0} \right\rangle, \]
при условии, что точки равномерно распределены по плоскости $(r, \varphi)$.

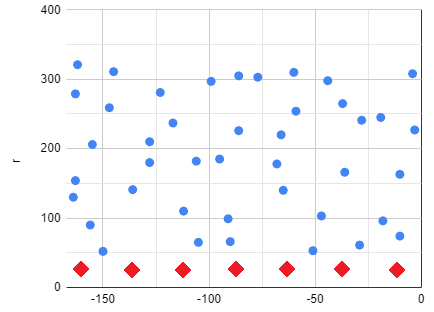
В итоге мы получили $\alpha = 0.17$, теоретическое значение $\alpha_\text{theory} = 0.16$. Если при численном интегрировании 2-мерной функции не было проверено распределение точек, то значение $\alpha$ обычно завышается. Например, если не учесть точки при $r/R \approx 0.1-0.2$, то $\alpha$ получается около $0.25$.

A3  ^0.50 Постройте график характеризующий Ваши измерения в координатах $r/R$ vs $\varphi/\pi$.

A4  ^0.20 Сравните полученный $\alpha$ с теоретической оценкой:
\[ \alpha_\text{theory} = \frac{4}{\pi^2} - \frac{1}{4}, \]
полученной в XIX веке лордом Рэлейем.

A5  ^0.30 По данным представленным на риснуке оцените собтсвенную частоту колебаний системы $\omega_0$ и ее добротность $1/\zeta$.

\[ \omega_0 = 2\pi \cdot 2.8 ~\text{Гц} = 18~1/\text{с}, \quad 1/\zeta = 1/22 \]

A6  ^0.70 Оцените $\alpha$ из спектральной характеристики колебаний.

Угловая частота колебаний физического маятника:
\[ \omega_0^2 = \frac{mga}{I}, \]
где $a$ — расстояние от центра масс до точки подвеса, $I$ — момент инерции. Для полукруга $a = \dfrac{4}{3\pi} R$, соотвественно тогда

\[ \omega_0 = 1.2 \sqrt{g/R} = \sqrt{\frac{2}{3\pi \alpha}} \sqrt{g/R}, \]
откуда $\alpha = 0.18$.

B1  ^0.30 Запишите II закон Ньютона для всей системы системы и уравнение вращательного движения для колец.

\[
\begin{cases}
M \ddot{x} + m \ddot{x} + ma \ddot{\theta} = F \\
MR \ddot{x} = -FR
\end{cases} \quad \Rightarrow \quad
2 M \ddot{x} + m \left( \ddot{x} + a \ddot{\theta} \right) = 0
\]

B2  ^0.20 Получите из уравнений предыдущего пункта уравнение, в котором есть только константы, параметры нашей системы и их производные.

B3  ^0.30 Запишите уравнение динамики вращательного движения для полуцилиндра, как дифференциальное уравнение второго порядка.

\[ I_0 \ddot{\theta} = -mga^2 \theta - ma \ddot{x} \]

B4  ^0.50 Найдите угловую частоту колебаний системы $\Omega$. Запишите решений полученной системы из двух уравнений, которое описывает то, как бутыка катиться рывками по плоскости.

\[ 1/\Omega^2 = \frac{a}{g} \left( \frac{I_0}{ma^2} - \frac{m}{2M+m}\right) \]

\[
\begin{cases}
\theta = A \sin\left( \Omega t + \phi_0\right) \\
x = -A \dfrac{ma}{2M + m} \sin \left( \Omega t + \phi_0\right)+ B t
\end{cases}
\]

B5  ^0.30 Пусть амплитуда колебаний скорости бутылки $\gamma v_0$ после отскока от стенки. Выразите $\gamma$ через известные велечины и $\eta$.

\[ I_0 \frac{\dot{\theta}_0}{2} = \left( m + M \right) \frac{v_0^2}{2} \]
\[ \gamma = \frac{ma}{2M+m}\sqrt{\eta \frac{m+M}{I_0}}=\frac{4}{3\pi} \cdot \frac{m}{2M+m} \sqrt{\eta} \sqrt{\frac{m+M}{2\alpha m}} \]

B6  ^1.50 Постройте график $\dot{x}/v_0$ vs $t$.

B7  ^0.20 Найдите экспериментальное значение $\Omega$, сравните его с теоретически.

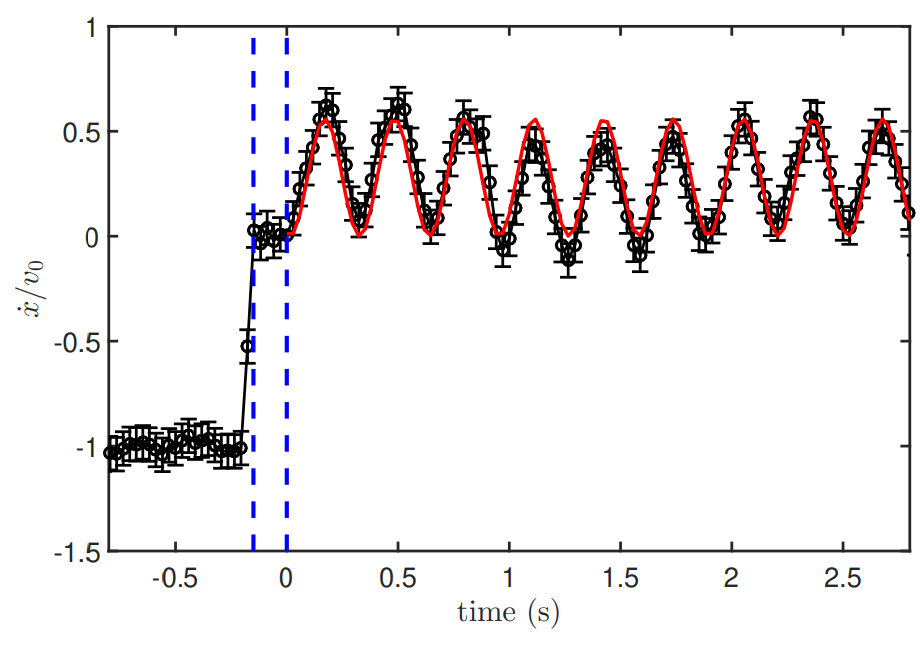
\[ \Omega_\text{theory} = 19.8~1/\text{с} \quad \Omega = 20.1~1/\text{с} \]

B8  ^0.30 Найдите значение $\eta$.

\[ \eta = 71\% \]