A1  ^0.30 Одна из моделей диэлектриков состоит в следующем: большое количество маленьких проводящих шариков радиусом $R$ заполняют пространство с концентрацией $n$, так, что $R^3 n \ll 1$. Определите, на сколько диэлектрическая проницаемость $\varepsilon$ отличается от единицы.

Проводящий шар, помещенный во внешнее поле, приобретает дипольный момент. Напряженность электрического поля $\vec{E}$ и дипольный момент шара $\vec{p}$ связаны соотношением

$$\vec{E} = -\frac{ \rho \vec{l} }{ 3 \varepsilon_0} = -\frac{ \vec{p} }{ 4 \pi R^3 \varepsilon_0} .$$

Вектор поляризации такой среды
$$\vec{P} = n\vec{p} = 4\pi \varepsilon_0 R^3 n \vec{E}.$$

Отличие диэлектрической проницаемости от единицы:

$$\varepsilon - 1 = \frac{P}{\varepsilon_0 E} = 4\pi n R^3.$$

B1  ^0.30 Уединённый диэлектрический шар радиуса $R$ поляризован так, что внутри него напряженность электрического поля однородна и равна $\vec{E}_{in}$. Определите напряженность электрического поля$ \vec{E}_{out} (\vec{r} )$, которое создаёт шар снаружи в точке $\vec{r}$. Радиус-вектор $\vec{r}$ проводится из центра шара.

Дипольный момент $\vec{p}$ шара связан с напряженностью однородного поля внутри $\vec{E}_{in}$:

$$\vec{p} = -4\pi \varepsilon_0 R^3 \vec{E}_{in}.$$

Снаружи – поле диполя:

$$\vec{E}_{out} = -R^3 \left( \frac{3(\vec{E}_{in}, \vec{r})\vec{r}}{r^5} - \frac{\vec{E}_{in}}{r^3}\right)$$

B2  ^1.00 Во внешнее однородное электрическое поле $\vec{E}_0$ поместили диэлектрический шар радиуса $R$. Напряженность электрического поля внутри шара стала равна $\vec{E}_0/n$. Определите диэлектрическую проницаемость материала шара $\varepsilon$.

Шар поляризуется так, что вектор поляризации $\vec{P}$внутри шара константа. Эти заряды создают поле:
$$\vec{E}_{пол} = -\frac{\vec{P}}{3\varepsilon_0}.$$
Поле внутри $\vec{E_1}$ есть сумма внешнего поля (до внесения шара) $\vec{E_0}$ и поля поляризационных зарядов:
$$\vec{E_1} = \frac{\vec{E}_0}{n} = \vec{E}_0 + \vec{E}_{пол}= \vec{E}_0 -\frac{\vec{P}}{3\varepsilon_0}.$$

Диэлектрическая проницаемость определяется следующим выражением:
$$\varepsilon \vec{E_1} = \vec{E_1} + \frac{\vec{P}}{\varepsilon_0}.$$

Подставив всё друг в друга, получаем ответ
$$\varepsilon = 3n-2.$$

B3  ^0.30 Если поместить неполярную частицу (например атом вещества) в электрическое поле $\vec{E'}$, то она приобретёт дипольный момент $\vec{p}$. Для малых полей эта зависимость линейная:
$$ \vec{p}= \beta \varepsilon_0 \vec{E'}.$$
Коэффициент $\beta$ называется «поляризуемость». Укажите поляризуемость $\beta$ для проводящего шара.

Для проводящего шара
$$\beta = 4\pi R^3.$$

C1  ^0.50 Если поместить атом водорода (который сам по себе не обладает дипольным моментом) в переменное электрическое поле $E(t)=E_0 \cos (⁡\omega t)$, то он поляризуется в основном за счёт того, что электрон массой $m_e$ и зарядом $q_e$ смещается под действием вынуждающей силы внешнего поля. То есть электрон совершает колебания возле положения равновесия (ядро атома). Определите, как зависит положение центра облака электрона от времени $x(t)$, если собственная частота таких колебаний электрона $\omega_0$?

Собственные колебания определяются некоторой возвращающей силой $F(x)=-k x$, которая определяет уравнение свободных колебаний:
$$m \ddot{x}+kx=0.$$

Поэтому эта возвращающая сила выражается через собственную частоту: $F(x) = - m \omega_0^2 x$.

В случае вынужденных колебаний
$$m \ddot{x}+m\omega_0^2 x = q_e E_0 \cos(\omega t)$$

ищем решение в виде колебаний с частотой вынуждающей силы $\omega$

$$x(t) = x_0 \cos (\omega t).$$

Подставив $x(t)$ в уравнение вынужденных колебаний найдем амплитуду. Окончательно, закон движения

$$x(t) = \frac{q_e E_0}{m(\omega^2_0 - \omega^2)} \cos (\omega t ).$$

C2  ^0.30 Если поместить указанный атом водорода в постоянное электрическое поле $E_0$, то он будет поляризоваться. Величина поляризации будет определяться собственной частотой колебаний $\omega_0$, которую можно оценить из следующих соображений: это частота электромагнитной волны, которая при поглощении атомом водорода ионизует его из основного состояния. Известно, что длина волны этого излучения $\lambda=91.1~нм$. Оцените поляризуемость $\beta$ атома водорода.

В постоянном поле $E_0$ у атома водорода возникает дипольный момент
$$p = q_e x_0 = \frac{q_e^2 E_0}{m \omega_0^2}.$$

Собственная частота колебаний связана с длиной волны падающего излучения
$$\omega_0 = \frac{2\pi c}{\lambda}.$$

Поляризуемость
$$\beta = \frac{q_e^2}{m \varepsilon_0} \cdot \left( \frac{\lambda}{2\pi c} \right)^2=7.4\cdot10^{-30}~м^3.$$

C3  ^0.30 Определите на сколько диэлектрическая проницаемость газообразного водорода отличается от единицы при атмосферном давлении и температуре $t=0^{\circ}\mathrm{C}$. Используйте значение поляризуемость атома водорода из предыдущего пункта. Для разряженных газов можно считать, что поле в веществе $E$ и поле которое действует на одну молекулу $E'$ совпадают.

$$\varepsilon -1 = \frac{P}{\varepsilon_0 E} = \frac{p n}{\varepsilon_0 E} = \beta n = \frac{\beta p_A}{k T} = 2.0\cdot 10^{-4}.$$

D1  ^0.50 Внутри сплошного однородного диэлектрика напряженность электрического поля равна $\vec{E}$, вектор поляризаций равен $\vec{P}$. Внутри диэлектрика вырезали сферическую полость. Определите напряженность электрического поля в веществе $\vec{E_h}$.

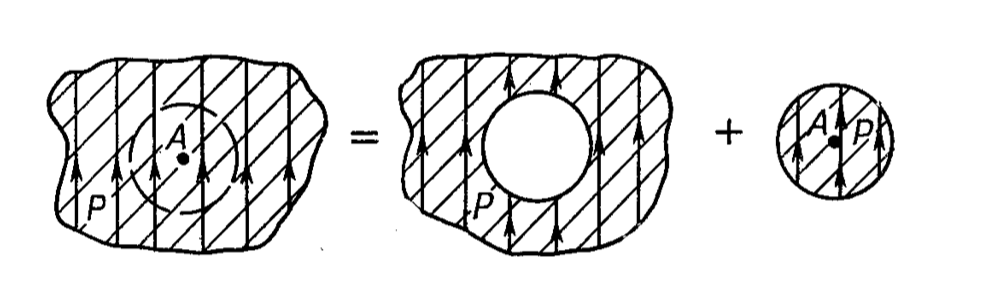
Поле внутри полости
$$\vec{E}_h = \vec{E} + \frac{\vec{P}}{3 \varepsilon_0}.$$

D2  ^1.00 Используя указанную выше модель найдите, на сколько диэлектрическая проницаемость жидкости $\varepsilon$ отличается от единицы. Концентрация молекул $n$, поляризуемость $\beta$.

В указанной выше модели Клаузиса-Моссотти дипольный момент атома $p$ определяется полем $E'=E_h$, поэтому вектор поляризации $P$ равен:

$$P = pn = \beta \varepsilon_0 n E_h.$$

Поле $E_h$ и поле в диэлектрике $E$ связаны соотношением
$$\vec{E}_h = \vec{E} + \frac{\vec{P}}{3 \varepsilon_0}.$$

Диэлектрическую проницаемость найдём из выражения
$$\varepsilon -1 = \frac{P}{\varepsilon_0 E}.$$

Объединяя всё это вместе получим ответ
$$\varepsilon - 1 = \frac{\beta n}{1- \beta n / 3}.$$

D3  ^0.50 Вещество Refrigerant-10 в газообразном виде имеет диэлектрическую проницаемость $\varepsilon_g=1.0030$ при температуре $t_g=105^{\circ}\textrm{C}$ и атмосферном давлении. Определите диэлектрическую проницаемость $\varepsilon_l$ данного вещества в жидком виде.

В газе

$$\varepsilon_g - 1 = \beta n_g.$$

В жидкости

$$\varepsilon_l - 1 = \frac{\beta n_l}{1 - \beta n_l/3}.$$

Отношение коэффициентов

$$\frac{\beta n_l}{\beta n_g} = \frac{\rho_{R10}}{\rho_{g}} = \frac{\rho_{
R10} RT}{p_A \mu_{R10}}.$$

$$\varepsilon_l =1+ \left( \frac{ p_A \mu_{R10}}{ (\varepsilon_g - 1) \rho_{R10} RT } - \frac{1}{3} \right)^{-1} = 2.44.$$

D4  ^0.50 Для воды при температуре $t_1=145^{\circ}\textrm{C}$ и атмосферном давлении диэлектрическая проницаемость равна $\varepsilon_1=1.00705$. Оцените диэлектрическую проницаемость воды $\varepsilon_2$ при температуре $t_2=20^{\circ}\textrm{C}$. Сравните результат полученный из этой модели с реальным значением диэлектрической проницаемости воды. Если он не сходится, укажите возможную причину.

При температуре $t_1 = 145 ^{\circ}\mathrm{C}$ и атмосферном давлении вода находится в газообразном состоянии. Поэтому

$$\varepsilon_1 - 1 = \beta n_1.$$

При $t_2 = 20 ^{\circ}\mathrm{C}$ вода жидкая:

$$\varepsilon_2- 1 = \frac{\beta n_2}{1 - \beta n_2/3}.$$

Отношение коэффициентов

$$\frac{\beta n_l}{\beta n_g} = \frac{\rho_w}{\rho_g} = \frac{\rho_w RT}{p_A \mu_w}.$$
$$\varepsilon_2 =1+ \left( \frac{ p_A \mu_w}{ (\varepsilon_1 - 1) \rho_w RT_1 } - \frac{1}{3} \right)^{-1} = -2.84.$$

Теория не совпадает с реальностью, потому, что не применима: молекула воды полярная, а теория для неполярных веществ из неполярных атомов/молекул.

E1  ^1.00 Определите разницу $\varepsilon-1$ для такого вещества с концентрацией молекул $n$ при температуре $T$.
Можно считать, что температура достаточно велика, а напряженность электрического поля не велика. Наведённый дипольный момент не учитывайте.

Энергия диполя в электрическом поле

$$U = - (\vec{p_0}, \vec{E}) = - p_0 E \cos \theta,$$

где $\theta$ – угол между $\vec{p}$ и $\vec{E}$.

Доля диполей, ориентированных под углом $\theta$ в некотором направлении, находится из распределения Больцмана:

$$w(\theta) = A e^{-U/kT} = A \exp \left( \frac{p_0 E \cos \theta}{kT} \right) \approx A \left(1+\frac{p_0 E \cos \theta}{kT} \right).$$

Вектор поляризации

$$P = n \frac{\int_0^\pi (p_0 \cos \theta) \cdot w(\theta) \cdot (2\pi \sin \theta d \theta)} {\int_0^\pi w(\theta) \cdot (2\pi \sin \theta d \theta)} .$$

В итоге эти интегралы сводятся к

$$P = n \frac{\int_0^\pi p_0^2 E/kT \cos^2 \theta \sin \theta d \theta} {\int_0^\pi \sin \theta d \theta} = \frac{n p_0^2 E}{3 k T}.$$

Ответ
$$\varepsilon-1 = \frac{n p_0^2}{3 \varepsilon_0 k T}$$

E2  ^1.00 По имеющимся данным таблицы определите дипольный момент молекулы $p_0$ и поляризуемость $\beta$ для воды. В таблице указана зависимость диэлектрической проницаемости воды от её температуры $T$ и давления $p$.

Заметим, что концентрация постоянно и равна $n = 1.40 \cdot 10^{25}~м^{-3}$.

Для полярного диэлектрика вклад от наведённых диполей и собственных складывается

$$\varepsilon-1 = \frac{n p_0^2}{3 \varepsilon_0 k T} + \frac{\beta n}{1- \beta n / 3}.$$

Данную зависимость можно лианеризовать координатами $\varepsilon-1$ от $1/T$, тогда коэффициент наклона

$$\frac{d(\varepsilon-1)}{d(1/T)} = \frac{n p_0^2}{3 \varepsilon_0 k} = 1.5052~К^{-1},$$

свободный член

$$(\varepsilon-1)_0 = \frac{\beta n}{1- \beta n / 3} = 16.666\cdot10^{-5}.$$

Отсюда

$$p_0 = 6.3 \cdot 10^{-30}~Кл \cdot м,$$

$$\beta = 1.2\cdot 10^{-29}~м^3 .$$