Рассмотрим классическую механическую систему с некоторым параметром $\lambda$, который может медленно меняться с течением времени. Если движение системы периодическое с периодом $T$, изменение параметра можно считать медленным при условии
$$
T\frac{d\lambda}{dt}\ll{\lambda}.
$$
В общем случае по временем $T$ можно понимать характерное время процессов, протекающих в системе.
Адиабатический инвариант — физическая величина, которая не меняется при плавном изменении параметров системы. Можно доказать, что адиабатическим инвариантом является величина
$$
I=\frac{1}{2\pi}\oint pdq.
$$
Здесь $p$ — одна из проекций импульса системы, $q$ — соответствующая координата.

Если изобразить периодическое движение частицы в координатах $p$, $q$, при периодическом движении получим замкнутую кривую. Тогда интеграл в определении $I$ равен площади, ограниченной этой кривой.

Часть A. Движение между двумя стенками (0.8 балла)

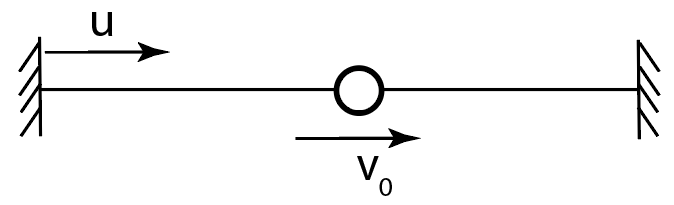
По гладкой горизонтальной спице между двумя вертикальными стенками может скользить бусинка массы $m$. Все удары бусинки со стенками абсолютно упругие. Одна стенка неподвижна, а вторая стенка движется по направлению к первой со скоростью $u$, удовлетворяющей соотношению $u\ll{v}$, где $v$ - скорость бусинки. Начальное расстояние между стенками равняется $L_0$, начальная скорость бусинки $v_0$.

A1  ^0.20 Найдите скорость бусинки сразу после соударения с подвижной стенкой.

A2  ^0.20 Найдите изменение расстояния между стенками за время между двумя последовательными соударениями бусинки с подвижной стенкой. Необходимо получить точную формулу.

A3  ^0.40 Найдите выражение для адиабатического инварианта $I$ для рассмотренной системы и определите скорость бусинки в момент, когда расстояние между стенками уменьшилось до значения $L$.

Часть B. Движение между стенкой и тяжёлой частицей (1.2 балла)

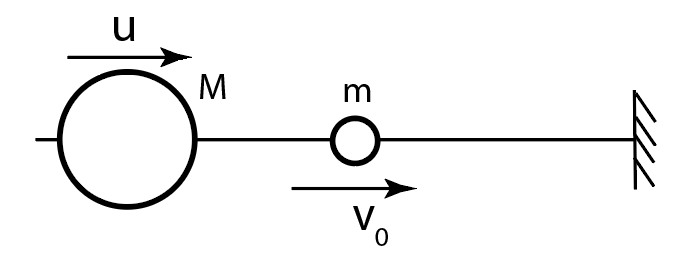
Данная часть задачи является фактическим продолжением предыдущей. Отличие состоит в том, что теперь на лёгкую частицу массы $m$, движущуюся со скоростью $v_0$ налетает со скоростью $u\ll{v_0}$ частица массы $M\gg{m}$. С другой стороны по-прежнему неподвижная стенка. Начальное расстояние между частицами равнялось $L_0$. Известно, что в процессе движения максимальная скорость легкой частицы равнялась $kv_0$. Массы частиц не даны!

B1  ^0.40 Выразите отношение масс $M/m$ через $u, v_0$ и $k$.

B2  ^0.80 Через какое время тяжёлая частица остановится? Ответ выразите через $L_0, v_0, u$ и $k$.

Часть C. Модель иона (1.5 балла)

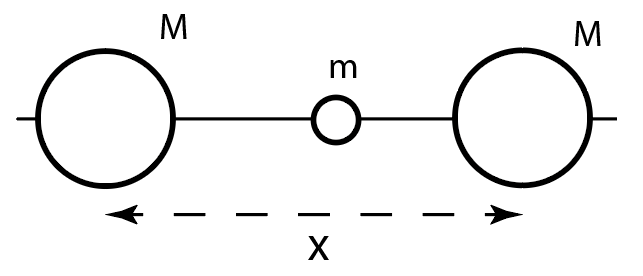
В данной части рассматривается упрощённая модель иона ${H_2}^+$. Две частицы массы $M$ и находящаяся между ними частица массы $m\ll{M}$ могут двигаться по гладкой горизонтальной спице. Лёгкая частица притягивается к тяжёлым с постоянными силами $F$. В момент, когда расстояние между тяжёлыми частицами равнялось $L_0$, скорость лёгкой частицы в системе отсчета центра масс двух тяжелых частиц равняется $v_0$. Вам предлагается исследовать положение равновесия данной системы, а также найти частоту её малых колебаний вблизи него. Обозначим расстояние между тяжелыми частицами за $x$.

C1  ^0.40 Получите выражение для кинетической энергии системы. Ответ выразите через $M, m, x, \dot{x}, v_0$ и $L_0$.

C2  ^0.20 Получите выражение для потенциальной энергии системы. Ответ выразите через $F$ и $x$.

C3  ^0.50 При каком значении $x$ система находится в положении равновесия? Ответ выразите через $M, m, v_0, L_0$ и $F$.

C4  ^0.40 Найдите циклическую частоту малых колебаний системы вблизи положения равновесия. Ответ выразите через $M, m, v_0, L_0$ и $F$.

Часть D. Движение внутри эллипса (2.2 балла)

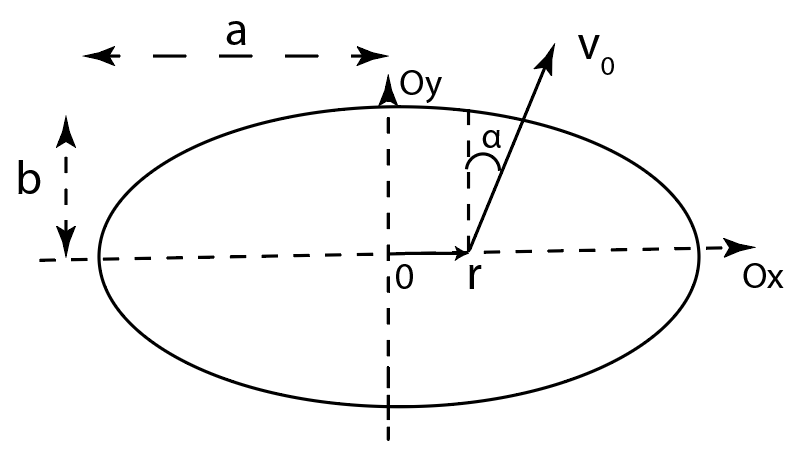
По гладкой горизонтальной поверхности ограниченной вертикальными стенками может свободно двигаться маленькая шайба. Стенки ограничивают часть поверхности в форме эллипса с большой и малой полуосями $a$ и $b$ соответственно. В положении с координатами $(r;0)$ шайбе сообщили скорость, проекции которой равны $v_x=v_0\sin\alpha; v_y=v_0\cos\alpha$, причём $r\ll{a,b}$, $\alpha\ll{1}$. От вас потребуется в первом приближении по этим малым параметрам описать движение шайбы.

D1  ^1.00 Можно показать, что в рассматриваемом приближении квадрат компоненты $v_x$ скорости шайбы зависит от координаты $x$ как $v^2_x=A+Bx+Cx^2$. Выразите $A, B$ и $C$ через $v_0$, $\alpha, a, b$ и $r$.

D2  ^0.60 Найдите максимальное значение координаты $x$ шайбы в процессе движения. Ответ выразите через $v_0$, $\alpha, a, b$ и $r$.

D3  ^0.60 Через какое время после запуска шайба впервые окажется в точке с координатой $x=0$? Какое условие на соотношение $a/b$ должно выполняться для применимости полученного результата?

Часть E.Математический маятник на наклонной плоскости (1.3 балла)

К гладкой наклонной плоскости привязан математический маятник, совершающий малые колебания вблизи положения устойчивого равновесия. В этой части задачи вам предлагается исследовать, как изменяется амплитуда колебаний маятника с изменением угла наклона плоскости, а также длины маятника. В начальный момент амплитуда колебаний (измеряется угол отклонения маятника от положения равновесия) равна $\varphi_0 \ll 1$, длина маятника равна $L_0$, а угол наклона плоскости равен $\alpha_0$.

E1  ^0.50 Найдите адиабатический инвариант $I$ для гармонического осциллятора с массой $m$, колеблющегося с циклической частотой $\omega_0$ и амплитудой $A$.

E2  ^0.40 Пусть при неизменном угле наклона длину маятника адиабатически медленно увеличили до $L$. Найдите новую амплитуду колебаний маятника $\varphi$. Ответ выразите через $\varphi_0, \alpha_0, L_0$ и $L$.

E3  ^0.40 Пусть при неизменной длине маятника угол наклона адиабатически медленно увеличили до значения $\alpha$. Найдите новую амплитуду колебаний $\varphi$. Ответ выразите через $\varphi_0, \alpha_0, \alpha$ и $L_0$.

Часть F. Ларморовская прецессия в медленно изменяющемся магнитном поле (2.5 балла)

Рассмотрим кольцо массы $M$,равномерно заряженное по периметру зарядом $q$, помещённое в однородное магнитное поле с индукцией $\vec{B_0}$. Кольцо раскрутили вокруг его оси до угловой скорости $\vec{\omega}$ и отпустили. Угол между векторами магнитной индукции и угловой скорости вращения кольца в начальный момент равен ${\alpha_0}$.
Примечание: Магнитный момент системы зарядов можно вычислить по формуле
$$\vec{m}=\int\frac{[\vec{r}\times\vec{v}]}{2}dq
$$

F1  ^0.20 Выразите вектор магнитного момента кольца $\vec{m}$ через $q$,$M$ и вектор его момента импульса относительно центра $\vec{L}$.

F2  ^0.20 Покажите, что модуль момента импульса $L$ остаётся постоянным.

F3  ^0.70 Покажите, что ось кольца испытывает прецессию и найдите вектор угловой скорости $\vec{\Omega}$ этой прецессии. Ответ выразите через $q$, $M$ и $\vec{B_0}$. Считайте, что $\Omega\ll{\omega}$.

F4  ^0.70 Магнитное поле адиабатически медленно начинают уменьшать со скоростью $\dot{B}$. Найдите момент сил (модуль и направление), действующих на кольцо со стороны вихревого электрического поля. В этом и следующем пункте считйте, что $\alpha_0=\pi/2$.

F5  ^0.70 Значение магнитного поля уменьшилось до $\vec{B_1}$. Найдите угол между осью вращения и направлением магнитного поля. Изменение угла можно считать малым.

Часть G. Движение в неоднородном магнитном поле (3.0 балла)

Одним из методов удержания частиц в магнитной ловушке в продольном (по полю) направлении состоит в использовании магнитных пробок, или магнитных зеркал, — областей, в которых напряжённость магнитного поля сильно (но плавно) возрастает. Такие области могут отражать налетающие на них вдоль силовых линий заряженные частицы. При движении заряженной частицы в "зеркальной" магнитной ловушке радиус траектории частицы уменьшается при продвижении в область сильного поля. В рамках двух последних частей мы изучим движение в таких полях.
Для магнитных зеркал определим коэффициент зеркальности $r_m$
$$r_m=\frac{B_{max}}{B_{min}}
$$
Во всех пунктах считайте, что траектории частиц представляют собой медленно изменяющиеся спирали с малым углом наклона, ведущие центры которых совпадают с силовыми линиями магнитного поля. Введём также компоненты скорости $v_{||}$ и $v_\perp$ ($v_{||}\ll v_{\perp}$), обозначающие компоненты скорости частицы, направленные вдоль и перпендикулярно направлению магнитного поля соответственно.

G1  ^0.20 Рассмотрим для начала плоское движение в однородном магнитном поле с индукцией $B_0$. Пусть его производная по времени равна $\dot{B}$ и изменение происходит адиабатически медленно. Начальная скорость частицы равна $v_0$,её масса $M$, а заряд $q$. Выразите тангенциальное ускорение частицы $\dot{{v_\perp}}$ через $M, q, v_0, B_0$ и $\dot{B}$.

G2  ^0.50 Пусть магнитное поле медленно изменило величину до значения $B$. Выразите скорость частицы $v_\perp$ через $v_0, B_0$ и $B$.

Перейдём к неоднородному магнитному полю. Поскольку ведущий центр траектории электрона перемещается вдоль силовой линии. Будем считать, что магнитное поле изменяется только в данном направлении.

G3  ^1.00 Пусть угол наклона винтовой линии равен $\alpha$ и мал. Покажите, что усреднённая по времени сила, действующая в направлении магнитного поля на заряд эквивалентна взаимодействию магнитного диполя с неоднородным полем. Найдите величину силы $F_{||}$. Ответ выразите через $m, v, q, B_z$ и $\frac{dB_z}{dz}$, где ось $z$ сонаправлена с магнитным полем.
Указание: Мы уже упоминали, что любые заряженные частицы обладают магнитным моментом. Поэтому вам достаточно рассмотреть контур с постоянным током, движущийся в неоднородном магнитном поле.

G4  ^0.70 Используя результаты предыдущих пунктов, определите зависимость угла $\alpha$ от величины магнитного поля $B$ Ответ выразите через $\alpha_0, B_0$ и $B$.

G5  ^0.60 Выразите максимально возможное значение угла $\alpha$ через $r_m$.

Часть H. Установка для реализации магнитного зеркала (2.5 балла)

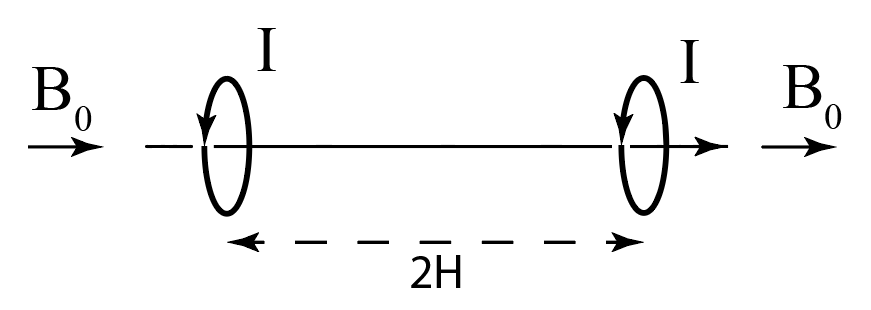
Мы изучили движение в неоднородных магнитных полях и готовы перейти к исследованию задачи о магнитных зеркалах. Схема, используемая для их реализации, представлена на рисунке. Она представляет собой два соосных витка одинакового радиуса $R$, центры которых находятся на расстоянии $2H\gg{R}$ друг от друга. По виткам протекают токи одинаковой силы $I$ в одном направлении. витки помещены в область большого однородного магнитного поля с индукцией $B_0$, направленного вдоль их осей. Целью данной задачи является исследование силовых линий такой системы и, как следствие, описание траектории ведущего центра орбиты электронов.

H1  ^0.40 Получите точную формулу зависимости индукции магнитного поля от координаты $x$. Начало координат находится по центру между витками, ось $x$ направлена вдоль магнитного поля. Найдите, учитывая малость некоторых параметров, также максимальное и минимальное значение суммарной индукции магнитного поля на оси витков.

H2  ^0.60 Найдите коэффициент зеркальности $r_m$ для данной системы. Учтите здесь и в дальнейшем, что $H\gg{R}$.

H3  ^1.00 Качественно нарисуйте силовую линию, проходящую через плоскость кольца на малом расстоянии $R_0\ll{R}$ от его оси в координатах $r'(x)$, где $r'$ — расстояние до оси симметрии системы. Найдите максимальное значение $r'$ и выразите ответ в виде: $r' \approx A + B (r-1)$.

H4  ^0.50 Найдите максимальное значение угла $\alpha$ в процессе движения, если отражения от магнитных зеркал происходит в плоскости колец. Считайте, что точки разворота частицы находятся достаточно близко к центрам колец. Учтите малость $r_m$.