A1  ^1.50 Найдите значение радиуса круговой орбиты $R_\text{ДПС}$, при котором механическое напряжение в области контакта объектов равняется нулю.
Величина $R_\text{ДПС}$ является пределом Роша $R_{Roche}$ для двойной планетарной системы

Пусть $\omega$ - угловая скорость вращения системы. Тогда из теоремы о движении центра масс получим:
$$2m\omega^2R=GMm\left(\displaystyle\frac{1}{(R-r)^2}+\displaystyle\frac{1}{(R+r)^2}\right)
$$
Рассмотрим отдельном условие движения центра ближнего объекта по окружности радиуса $R-r$:
$$m\omega^2(R-r)=\displaystyle\frac{GMm}{(R-r)^2}+N-\displaystyle\frac{Gm^2}{4r^2}
$$
Комбинируя, находим:
$$N=\displaystyle\frac{Gm^2}{4r^2}+\displaystyle\frac{GMm}{2R}\left(\displaystyle\frac{R-r}{(R+r)^2}-\displaystyle\frac{R+r}{(R-r)^2}\right)
$$
Учитывая, что $R_0\gg{r}$, находим:
$$N\approx{\displaystyle\frac{Gm^2}{4r^2}-\displaystyle\frac{3GMmr}{R^3}}
$$
Сила механического взаимодействия между объектами неотрицательна при
$$R\geq{r\sqrt[3]{\displaystyle\frac{12M}{m}}}
$$
Тогда для $R_{ДПС}$ имеем:

B1  ^0.70 Получите точное выражение для суммарного потенциала $\varphi_\text{внеш}$ в поле центробежной силы и гравитационного поля планеты. Ответ выразите через $x$, $y$, $z$, $G$, $\rho_M$, $R_0$ и $R$.

Орбитальная угловая скорость движения спутника $\omega$ равна
$$\omega=\sqrt{\cfrac{GM}{R^3}}
$$
где $M=\cfrac{4\pi R^3_0\rho_M}{3}$.
Потенциальная энергия частицы массой $m$ в поле центробежной силы (считаем её равной нулю на оси вращения) равна
$$W_p=-\frac{m\omega^2r^2_{\perp}}{2}
$$
где $r_{\perp}$ - расстояние от частицы до оси вращения.
Тогда для потенциала имеем:
$$\varphi=-\cfrac{4\pi R^3_0\rho_MG}{3R}\left(\cfrac{R}{r}+\cfrac{r^2_\perp}{2R^2}\right)-\varphi_O
$$
откуда:

B2  ^0.80 В приближении $x,y,z\ll{R}$ выражение для потенциала $\varphi$ можно представить в следующем виде:
$$\varphi_{\text{внеш}}=A_1x^2+B_1y^2+C_1z^2
$$
Найдите коэффициенты $A_1$, $B_1$ и $C_1$. Ответы выразите через $R$, $G$, $R_0$ и $\rho_M$.

Для разложения $\cfrac{R}{\sqrt{(R+x)^2+y^2+z^2}}$ имеем:
$$\cfrac{R}{\sqrt{(R+x)^2+y^2+z^2}}\approx{1-\frac{x}{R}-\frac{x^2+y^2+z^2}{2R^2}}+\frac{3x^2}{2R^2}
$$
Подставляя в выражение для $\varphi$, получим:
$$\varphi=-\cfrac{2\pi R^3_0\rho_MG}{R^3}x^2+\cfrac{2\pi R^3_0\rho_MG}{3R^3}z^2
$$
Таким образом:

C1  ^0.80 Докажите, что гравитационное поле внутри полости равняется нулю.

Обратимся к доказательству равенства нулю в полости шара, концентричной ему.
Рассмотрим некоторую точку полости $A$. выделим два элементарных объёма $dV_1$ и $dV_2$, поля которых компенсируют друг-друга:
$$\frac{dV_1}{r^2_1}=\frac{dV_2}{r^2_2}
$$
Произвольных эллипсоид может быть получен сжатием из сферы вдоль взаимно перпендикулярных осей.
Поскольку объём любого элементарного параллелепипеда $dV=dxdydz$, все элементарные объёмы уменьшаются в одно и то же число раз.
Также сохранятся и соотношения расстояний между точками.
Тогда, поскольку внутри полости шара суммарное гравитационное поле равно нулю, то нулю равно и гравитационное поле внутри полости эллипсоида.

C2  ^0.40 Пусть потенциал в центре эллипсоида равен $\varphi_0$.
Рассмотрим точку внутри эллипсоида, радиус-вектор относительно центра равен $\vec{r}$. Потенциал в данной точке равен $\varphi_1$.
Чему в также лежащей внутри эллипсоида точке с радиус-вектором $\gamma\vec{r}$ равен потенциал $\varphi_2=\varphi(\gamma\vec{r})$?
Ответ выразите через $\varphi_0$, $\varphi_1$ и $\gamma$.

Рассмотрим точки $1$ и $2$, лежащие на одной прямой, проходящей через центр эллипсоида. Пусть расстояния от центра эллипсоида до этих точек равны $r_1$ и $r_2$ соответственно, а рассматриваемая прямая составляет угол $\alpha$ с осью $x$.
Обе точки принадлежат границам подобных рассматриваемому эллипсоидов с некоторыми коэффициентами $k_1$ и $k_2$. Поскольку внутри эллипсоидальных полостей гравитационное поле равняется нулю, разность потенциалов между точкой $1$ и центром рассматриваемого эллипсоида $\varphi_1-\varphi_0=f(\alpha)r^2_1$, а также $\varphi_2-\varphi_0=f(\alpha)r^2_2$, где $f(\alpha)$ - некоторая функция, зависящая только от угла $\alpha$.
Отсюда находим:

C3  ^1.00 Покажите, что в точке эллипсоида с координатами $x,y,z$ потенциал можно представить в виде:
$$\varphi=\varphi_0+A_2x^2+B_2(y^2+z^2)
$$
$\textit{Примечание:}$ обратите внимание, что данное выражение применимо для эллипсоидов сколь угодно малых размеров

Расстояния $r$ могут быть сколь угодно малыми. Рассмотрим точки, близкие к центру эллипсоида. Для них:
$$\vec{g}=\frac{\partial\vec{g}}{\partial x}dx+\frac{\partial\vec{g}}{\partial y}dy+\frac{\partial\vec{g}}{\partial z}dz
$$
где все производные берутся в начале координат. Поскольку эллипсоид - симметричная фигура для точек лежащих на осях $x$, $y$ и $z$ верно соответственно.
$$\frac{\partial\vec{g}}{\partial x}=\frac{\partial g_x}{\partial x}\vec{e}_x\quad\frac{\partial\vec{g}}{\partial y}=\frac{\partial g_y}{\partial y}\vec{e}_y\quad\frac{\partial\vec{g}}{\partial z}=\frac{\partial g_z}{\partial z}\vec{e}_z
$$
отсюда найдём:
$$\frac{\partial g_r}{\partial r}=-2f(\alpha)=(\vec{e}_r\cdot{\vec{e}_x})\frac{\partial g_x}{\partial x}\frac{\partial x}{\partial r}+(\vec{e}_r\cdot{\vec{e}_y})\frac{\partial g_y}{\partial y}\frac{\partial y}{\partial r}+(\vec{e}_r\cdot{\vec{e}_z})\frac{\partial g_z}{\partial z}\frac{\partial z}{\partial r}
$$
Пусть $g_\perp$ - компонента гравитационного поля эллипсоида, перпендикулярная оси $x$.

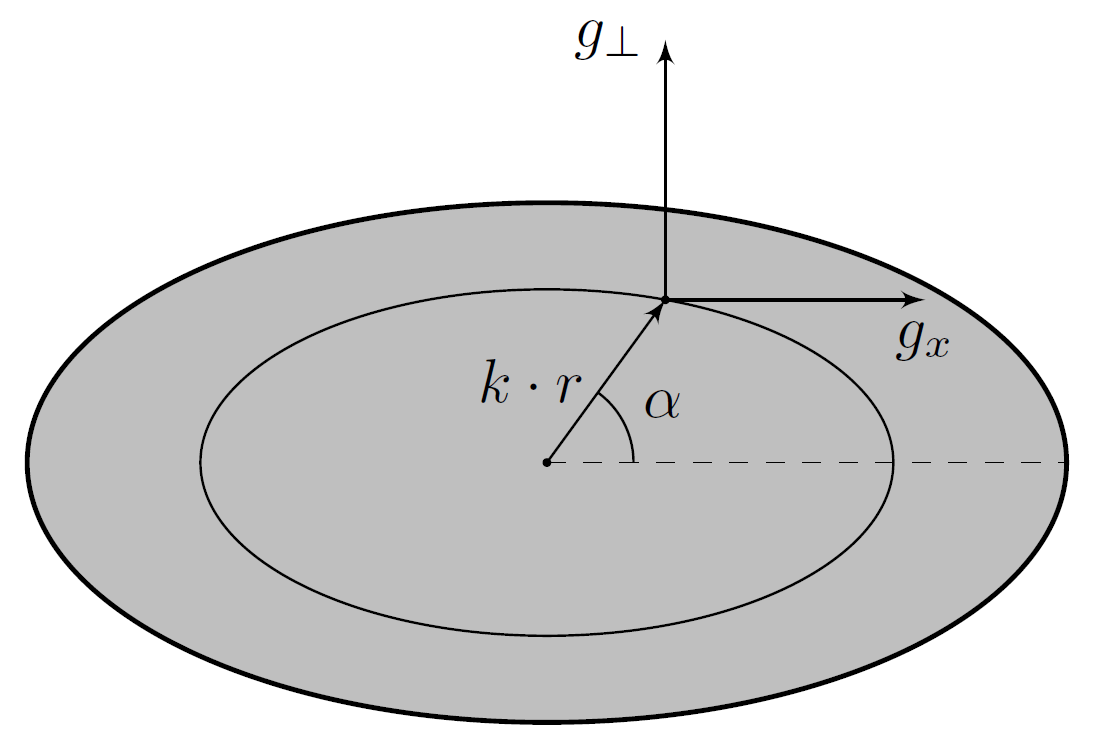
Учитывая, что для эллипсоида вращения $\cfrac{\partial g_y}{\partial y}=\cfrac{\partial g_z}{\partial z}=\cfrac{\partial g_\perp}{\partial r_\perp}$, получим
$$-2f(\alpha)=\frac{\partial g_x}{\partial x}\cos^2\alpha+\frac{\partial g_\perp}{\partial r_\perp}\sin^2\alpha
$$
Поскольку соотношение верно для любых $\alpha$, все частные производные должны оставаться постоянными в любой точке эллипсоида.
Подставляя в выражение для потенциала, найдём:

C4  ^0.30 Выразите $B_2$ через $A_2$, $G$ и $\rho$.
$\textit{Примечание:}~$ воспользуйтесь теоремой Гаусса в дифференциальной форме для гравитационного поля:
$$\displaystyle\frac{\partial^2{\varphi}}{\partial{x}^2}+\displaystyle\frac{\partial^2{\varphi}}{\partial{y}^2}+\displaystyle\frac{\partial^2{\varphi}}{\partial{z}^2}=4\pi\rho G
$$

Из теоремы Гаусса в дифференциальной форме находим:
$$\frac{\partial g_x}{\partial x}+\frac{\partial g_y}{\partial y}+\frac{\partial g_z}{\partial z}=-2A_2-4B_2=-4\pi G\rho
$$
откуда:

C5  ^0.30 Потенциал $\varphi$ на поверхности эллипсоида можно представить как функцию только координаты $x$ в следующем виде:
$$\varphi=C_2+x^2D_2
$$
Выразите $C_2$ и $D_2$ через $\varphi_0$, $A_2$, $G$, $\rho$, $a$, $x$ и эксцентриситет $e$.

$$y^2+z^2=a^2(1-e^2)-(1-e^2)x^2
$$
откуда:
$$\varphi=\varphi_0+\left(\pi\rho G-\cfrac{A_2}{2}\right)a^2(1-e^2)+\left(\cfrac{A_2(3-e^2)}{2}-\pi\rho G(1-e^2)\right)x^2
$$

C6  ^0.50 Решим вспомогательную задачу: по поверхности диска радиуса $R$ равномерно распределена масса с поверхностной плотностью $\sigma$.
Найдите потенциал диска $\varphi_\text{д}$ на оси на расстоянии $x$ от его центра.
Ответ выразите через $\sigma$, $G$, $R$ и $x$.

Разобьём диск на кольца:
$$\varphi_\text{д}=-\pi\sigma G\int\limits_0^R\frac{2rdr}{\sqrt{r^2+x^2}}
$$

C7  ^1.00 Найдите потенциал $\varphi_0$ в центре эллипсоида. Ответ выразите через $G$, $\rho$, $a$ и $e$.
$\textit{Примечание:}$ вам может понадобиться следующий интеграл: $$\displaystyle\int\sqrt{1+x^2}dx=\cfrac{x\sqrt{1+x^2}+\ln\left(x+\sqrt{1+x^2}\right)}{2}+C
$$

Разобьём эллипсоид на диски, при этом учтём, что $d\sigma=\rho dx$:
$$\varphi_0=-2\pi\rho G\cdot{2\int\limits_{0}^a\left(\sqrt{x^2+y^2+z^2}-x\right)dx}
$$
Интеграл от второго слагаемого равен $-\cfrac{a^2}{2}$. Подставим $y^2+z^2$ из уравнения эллипсоида:
$$\varphi=2\pi\rho Ga^2-4\pi\rho G\int\limits_{-a}^a\sqrt{b^2+\frac{c^2x^2}{a^2}}dx=2\pi\rho Ga^2-\frac{4\pi\rho G ab^2}{c}\int\limits_0^{\frac{c}{b}}\sqrt{1+t^2}dt
$$
Воспользуемся первообразной:
$$\varphi_0=2\pi\rho Ga^2-\frac{2\pi\rho G ab^2\left(\cfrac{ac}{b^2}+\ln\left(\cfrac{a+c}{b}\right)\right)}{c}
$$
Выразим через эксцентриситет:

C8  ^1.00 Найдите потенциал эллипсоида $\varphi_a$ в точке с координатами $(x, y, z)=(a, 0, 0)$. Ответ выразите через $G$, $\rho$, $a$ и $e$.
$\textit{Примечание:}$ вам может понадобиться следующий интеграл: $$\displaystyle\int\sqrt{x^2-1}dx=\cfrac{x\sqrt{x^2-1}-\ln\left(x+\sqrt{x^2-1}\right)}{2}+C
$$

Вновь разобьём эллипсоид на диски:
$$\varphi_a=-2\pi\rho G\int\limits_{-a}^{a}\left(\sqrt{(a+x)^2+y^2+z^2}-(x+a)\right)dx
$$
Интеграл от второго слагаемого равен $-2a^2$. Подставим $y^2+z^2$ из уравнения эллипсоида и преобразуем:
$$\int\limits_{-a}^{a}\sqrt{(a+x)^2+y^2+z^2}dx=\int\limits_{-a}^{a}\sqrt{\left(\frac{cx}{a}+\frac{a^2}{c}\right)^2-\frac{b^4}{c^2}}dx=\frac{ab^4}{c^3}\int\limits_{\frac{a^2-c^2}{b^2}}^{\frac{a^2+c^2}{b^2}}\sqrt{t^2-1}dt=
$$
$$=\frac{a^2(1-e^2)^2}{e^3}\int\limits_{1}^{\frac{1+e^2}{1-e^2}}\sqrt{t^2-1}dt=a^2\left(\frac{(1+e^2)}{e^2}-\frac{(1-e^2)^2}{e^3}\ln\sqrt{\frac{1+e}{1-e}}\right)
$$
откуда:

C9  ^0.20 Найдите коэффициент $A_2$. Ответ выразите через $G$, $\rho$ и $e$.

$$\varphi_a-\varphi_0=A_2a^2=2\pi\rho Ga^2\left(\frac{1-e^2}{e^3}\ln\sqrt{\frac{1+e}{1-e}}-\frac{(1-e^2)}{e^2}\right)
$$
откуда

D1  ^0.70 Постройте на листе миллиметровой бумаги график зависимости коэффициента $D_2$ от эксцентриситета $e$ эллипсоида, образованного спутником.

Подставим $A_2$ в выражение для $D_2$:
$$D_2=\pi\rho G~\frac{1-e^2}{e^3}\left((3-e^2)\ln\sqrt{\frac{1+e}{1-e}}-3e\right)
$$

D2  ^0.30 При каком значении эксцентриситета $e$ предел Роша достигается?

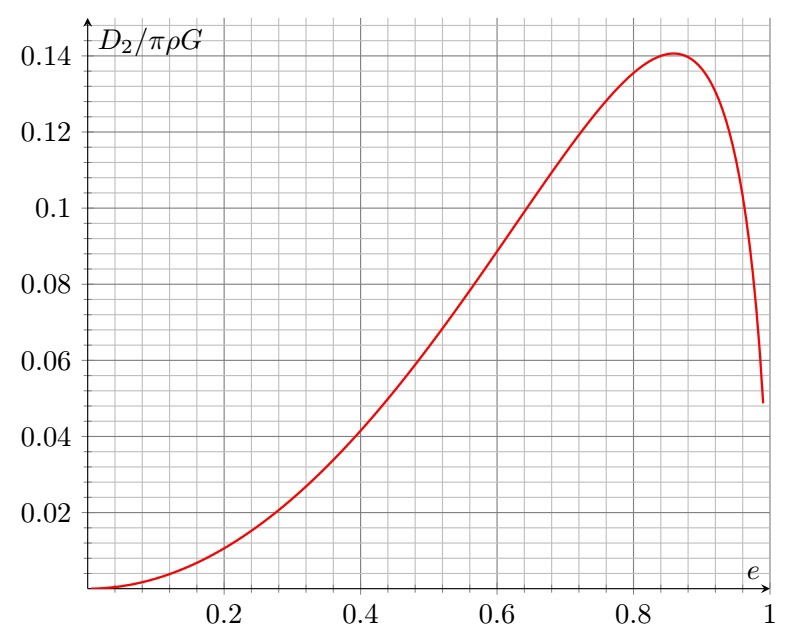
При достижении функцией $D_2$ максимума дальнейшее уменьшение радиуса круговой орбиты является невозможным, поэтому спутник разрушается.
Мысль о решении уравнения для равной нулю производной не является разумной.

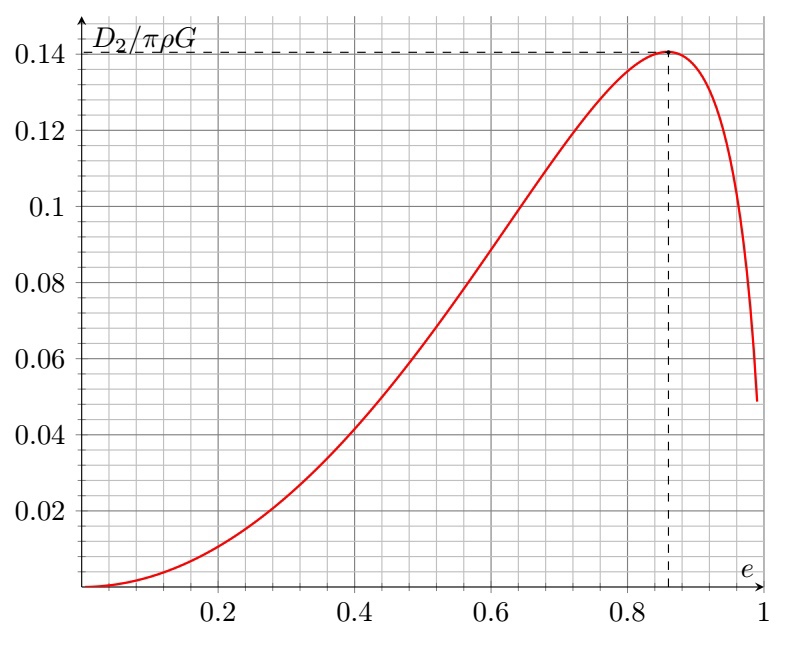
Из графика находим:

D3  ^0.50 Найдите предел Роша $R_{Roche}$. Ответ выразите через $R_0$, $\rho_M$ и $\rho_m$.

Значение $D_2$ в экстремуме равняется
$$D_{2_{max}}\approx{0,14\pi\rho_m G}
$$
откуда: