
Поле цилиндра можно представить как сумму полей бесконечно длинных тонких нитей (узких полосок), заряженных с постоянной линейной плотностью заряда $\lambda$. Найдём поле такой нити на расстоянии $r$ от нее, воспользовавшись симметрией поля и теоремой Гаусса
$$\Phi=2{\pi}rLE_r=\frac{q}{\epsilon_0}=\frac{\lambda{L}}{\varepsilon_0}
$$
откуда следует:
$$E_r=\frac{\lambda}{2{\pi}r\varepsilon_0}.
$$
Найдём напряжённость поля в точке с координатами $(x;~0)$. Рассмотрим два выделенных на рисунке небольших участка цилиндра.
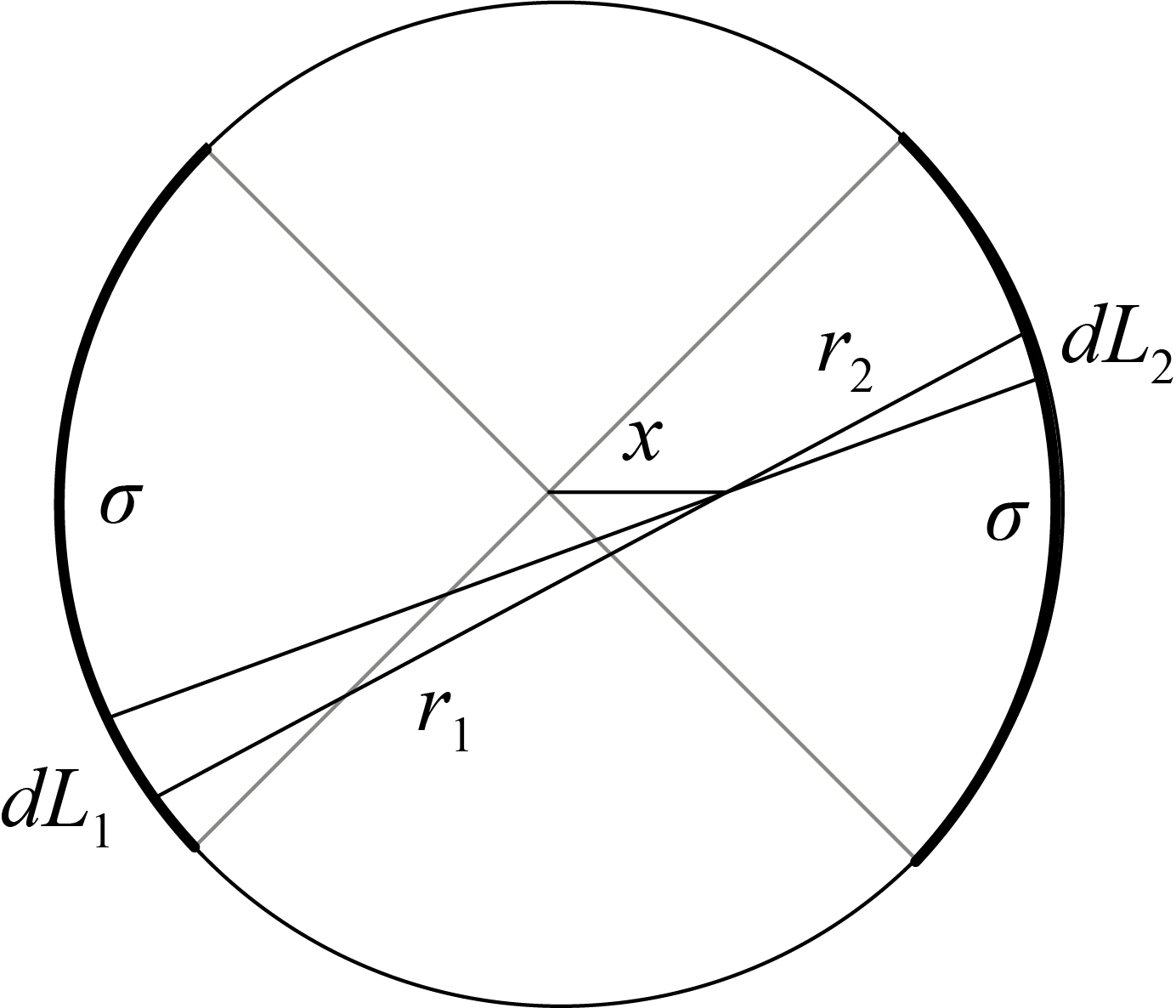
Они создают противоположно направленные поля как от двух нитей с линейными плотностями заряда $\sigma{dL_1}$ и $\sigma{dL_2}$ соответственно. Из подобия треугольников имеем:
$$\frac{dL_1}{r_1}=\frac{dL_2}{r_2},
$$
поэтому
$$dE_1=\frac{\sigma{dL_1}}{2{\pi}r_1\varepsilon_0}=\frac{\sigma{dL_2}}{2{\pi}r_2\varepsilon_0}=dE_2,
$$
и эти два поля друг друга компенсируют. Исходя из этого ясно, что поле цилиндра в рассматриваемой точке эквивалентно суммарному полю двух выделенных полосок шириной $dS$ каждая, поля которых не компенсируются (см.рис.)
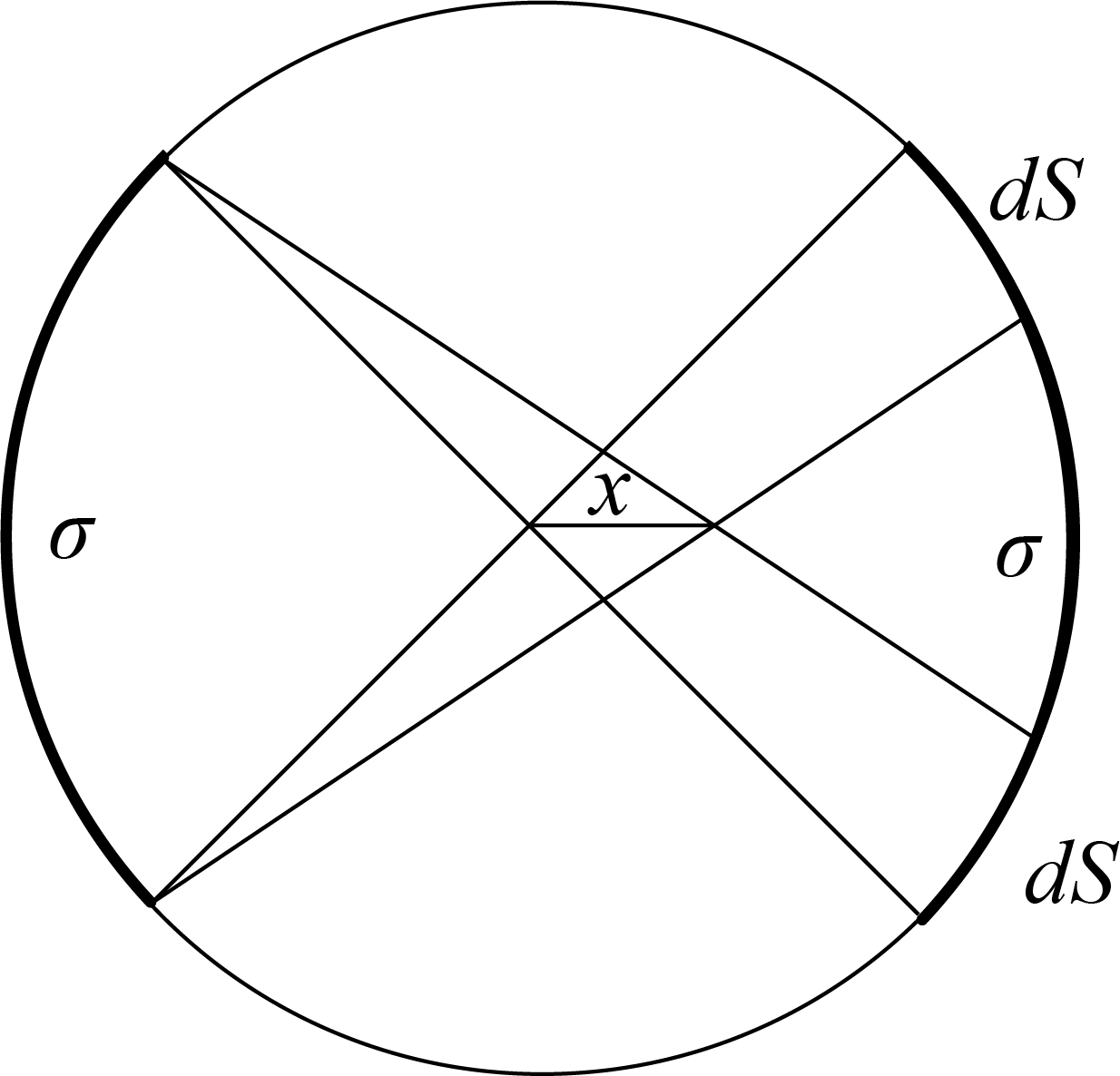
При этом
$$dS=x\sqrt{2},
$$
и каждая полоска создаёт поле, равное
$$E_0=\frac{\sigma{x}\sqrt{2}}{2{\pi}R\varepsilon_0}
$$
Поля этих полосок компенсируют друг друга в направлении оси $y$, поэтому $E_y=0$, а проекция поля на ось $x$ равна
$$E_x=2\cdot{\frac{-E_0}{\sqrt{2}}{}}=-\frac{\sigma{x}}{{\pi}R\varepsilon_0}.
$$
Таким образом, результирующее поле направлено к оси цилиндра.
Для нахождения поля в точке $(0,y)$ представим исходный цилиндр как суперпозицию полностью заряженного цилиндра с поверхностной плотностью заряда $+\sigma$ и двух четвертинок с поверхностной плотностью $-\sigma$ (см рис.)
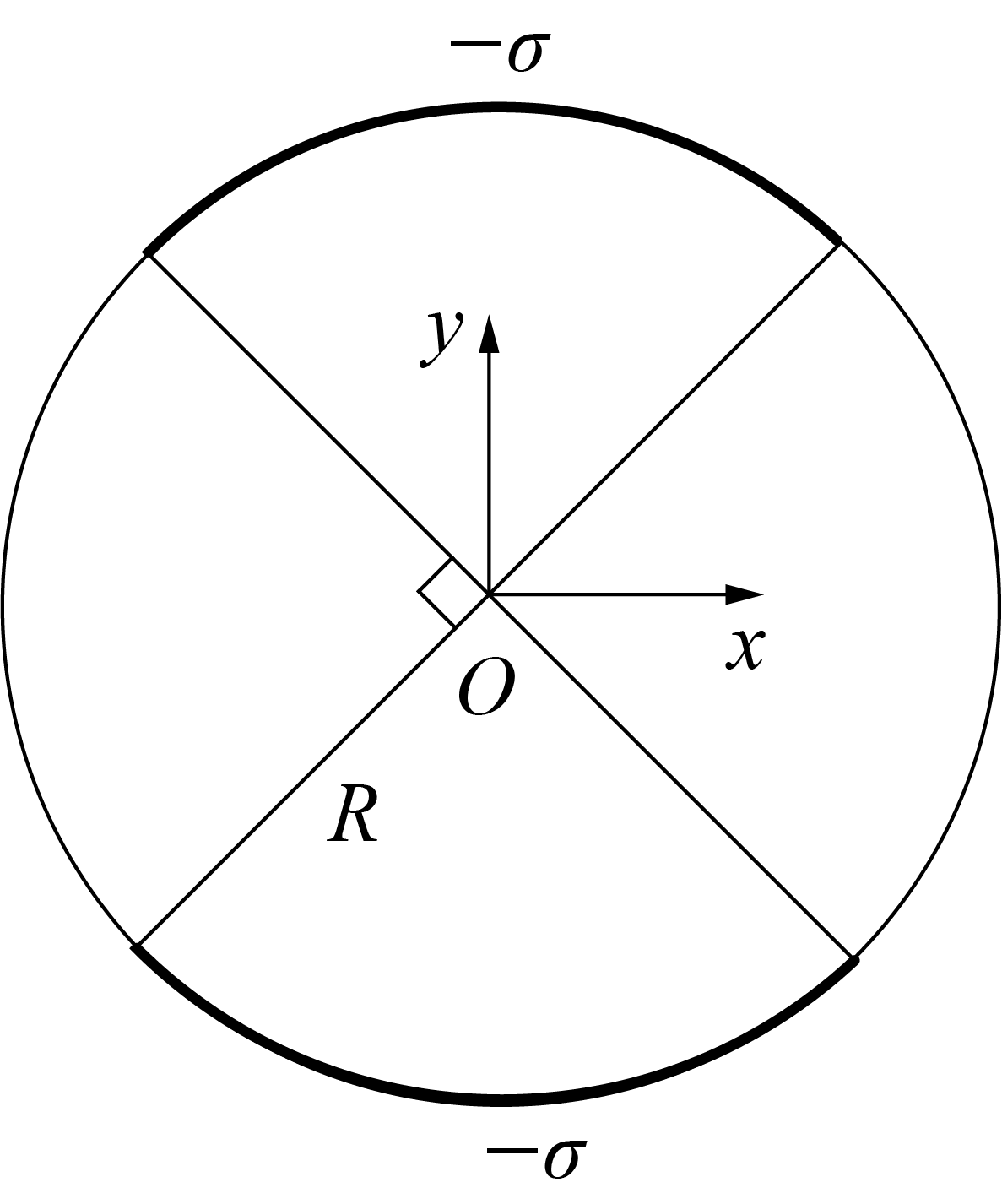
Поле $E_1$, создаваемое двумя отрицательно заряженными четвертинками, аналогично, найденному в первом случае, поэтому можем воспользоваться готовым результатом:
$$E_{1_y}=\frac{\sigma{y}}{{\pi}R\varepsilon_0};~E_{1_{x}}=0
$$
Поле, создаваемое в точке $(y,0)$, равномерно заряженным цилиндром из соображений симметрии и теоремы Гаусса равно нулю. Тогда по принципу суперпозиции проекции результирующего поля $E'$ в искомой точке равны:
$${E_y}'=\frac{\sigma{y}}{{\pi}R\varepsilon_0};~{E_x}'=0.
$$
Поле $E'$ направлено от оси цилиндра.