Pho.rs: Пластина с шайбой

1 ^4.00 Определите напряженность электрического поля в точке $A$.

I способ

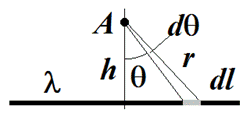
Напряженность электрического поля определяется скоростью изменения потенциала: $E=\left|\frac{\Delta \varphi }{\Delta h}\right|$. Найти разность потенциалов от стержня в точках $А$ и $А'$, расстояние между которыми $\Delta h$ — это то же самое, что найти разность потенциалов в точке $A$ от двух стержней, смещенных на расстояние $\Delta h$.

Рассмотрим вклады в потенциал от малых элементов стержней, видимых из центра под равными углами. Потенциал точечного заряда определяется соотношением $\varphi =\cfrac{q}{4\pi {\varepsilon }_0r}$.Поскольку линейные плотности зарядов одинаковы, то отношение потенциалов от таких элементов будет следующим$\cfrac{{\varphi }_1}{{\varphi }_2}=\cfrac{l_1}{l_2}\cfrac{r_2}{r_1}$. Из подобия треугольников следует, что данное отношение равняется единице. Таким образом, разность потенциалов от двух стержней, находящихся на расстоянии $\Delta h$, равна потенциалу от двух частей на краях одного из стержней. Длина каждой из них $\Delta l=\Delta h{\mathrm{tg} \varphi \ }$, находятся они на расстоянии $r=\cfrac{h}{{\cos \varphi \ }}$ от точки $А$, откуда $\mathrm{\Delta }\varphi =\cfrac{2\lambda \mathrm{\Delta }l}{4\pi {\varepsilon }_0r}=\cfrac{\lambda \Delta h{\sin \varphi \ }}{2\pi {\varepsilon }_0h}$, и

Ответ: \[E=\frac{\lambda {\sin \varphi \ }}{2\pi {\varepsilon }_0h}\]

II способ

Если элемент стержня виден из точки $A$ под углом $d\theta $, то длина этого элемента $dl=\cfrac{rd\theta }{{\cos \theta \ }}$, где $\theta $ — угол между направлением на элемент и перпендикуляром, опущенным из точки A на стержень, $r=\cfrac{h}{{\cos \theta \ }}$ — расстояние от элемента до точки $A$. Тогда напряженность электрического поля, создаваемого этим элементом, равна $\cfrac{\lambda dl}{4\pi {\varepsilon }_0r^2}$, а его проекция на перпендикуляр
\[dE=\cfrac{\lambda dl{\cos \theta \ }}{4\pi {\varepsilon }_0r^2}=\cfrac{\lambda {\cos \theta \ }d\theta }{4\pi {\varepsilon }_0h}\]
Суммируя эти проекции для всех элементов, получаем $$E=\int^{\varphi }_{-\varphi }{\cfrac{\lambda {\cos \theta \ }d\theta }{4\pi {\varepsilon }_0h}}=\cfrac{\lambda {\sin \varphi \ }}{2\pi {\varepsilon }_0h}$$

2.1 ^5.00 Определите величину и направление ускорения шайбы сразу после того, как ее отпустили.

При отклонении от центра взаимодействие частицы с пластиной можно представить как взаимодействие с прямоугольником максимально большого размера с центром в положении частицы и с двумя оставшимися тонкими полосами (см. рис). Прямоугольник не имеет составляющей поля в плоскости квадрата в силу симметрии, значит, эта составляющая определяется только полями полосок.Толщины полос равны удвоенным смещениям частицы вдоль направлений, перпендикулярных им.Поскольку $r\ll L$, воспользуемся результатом части 1 и заменим полоски на стержни с линейной плотностью заряда ${\lambda }_1=2r\sigma {\sin \alpha \ }$ и ${\lambda }_2=2r\sigma {\cos \alpha \ }$. Напряженность поля от каждой из них равна $E_{1,2}=\cfrac{{\lambda }_{1,2}}{2\sqrt{2}\pi {\varepsilon }_0(L/2)}$, поскольку стержни видны из центра квадрата под углом $2\varphi =\pi /2$. Эти напряженности перпендикулярны (каждая направлена перпендикулярно своему стержню), поэтому складывая их, получаем

$$E=\frac{\sqrt{{\lambda }^2_1+{\lambda }^2_2}}{\sqrt{2}\pi {\varepsilon }_0L}=\frac{\sqrt{2}r\sigma }{\pi {\varepsilon }_0L}$$

\noindent Из отношения $\cfrac{E_1}{E_2}={\mathrm{tg} \alpha \ }$ получаем, что суммарное поле направлено под углом $\alpha $ к стороне — от центра квадрата. Шайба будет притягиваться к центру, поскольку заряды пластины и шайбы разноимённые. Таким образом, ускорение шайбы будет направлено к точке $O$ и равно

Ответ: \[a=\frac{\sqrt{2}r\sigma }{\pi {\varepsilon }_0mL}\]

2.2 ^3.00 Через какое время шайба впервые окажется на минимальном расстоянии от центра пластины?

Движение шайбы под действием данного поля эквивалентно движению под действием пружины с коэффициентом жёсткости $k=\cfrac{\sqrt{2}\sigma q}{\pi {\varepsilon }_0L}$. Движение будет гармоническим с периодом $T=2\pi \sqrt{\cfrac{m}{k}}=\sqrt{\cfrac{2\sqrt{2}{\pi }^3{\varepsilon }_0mL}{\sigma q}}$, а траектория будет проходить через центр квадрата.

Ответ: Впервые шайба окажется в центре через время $t=\cfrac{T}{4}=\sqrt{\cfrac{{\pi }^3{\varepsilon }_0mL}{4\sqrt{2}\sigma q}}$

Пластина с шайбой

Решение