2
??
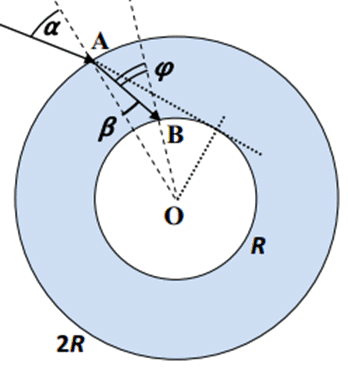
Показатель преломления вещества шара линейно уменьшается при увеличении расстояния $r$ от центра: $n(r)=2.5-0.5\frac{r}{R}, R\le r \le 2R$.
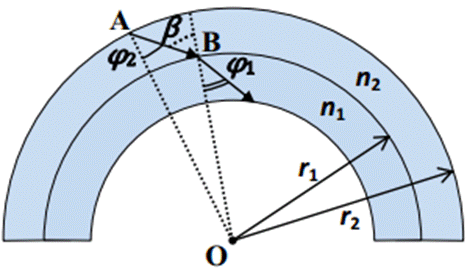
Анализ второго случая начнем с построения закона изменения направления светового луча в сферически-симметричной среде с переменной оптической плотностью. Рассмотрим прохождение луча через тонкий сферический слой, внутренний и внешний радиусы которого равны $r_1$ и $r_2$. Будем считать в пределах этого слоя показатель преломления постоянным и равным $n_2$, а под его внутренней поверхностью — равным $n_1$ (рисунок 3). Пусть световой луч входит в этот слой под углом ${\varphi }_2$ к радиусу, проведенному в точку входа А. Тогда угол его падения $\beta $ на внутреннюю поверхность слоя снова может быть определен из теоремы синусов: $\cfrac{r_2}{\mathrm{sin}\mathrm{}(\pi -\beta )}=\cfrac{r_1}{\mathrm{si}\mathrm{n}\mathrm{}({\varphi }_2)}$, то есть ${\mathrm{sin} \left(\beta \right)\ }=\cfrac{r_2}{r_1}\mathrm{sin}\mathrm{}({\varphi }_2)$. Угол наклона луча к радиусу после перехода в следующий слой определяется из закона преломления ${\mathrm{sin} \left({\varphi }_1\right)=\cfrac{n_2}{n_1}\mathrm{sin}\mathrm{}(\beta )\ }=\cfrac{n_2r_2}{{n_1r}_1}\mathrm{sin}\mathrm{}({\varphi }_2)$, и мы обнаруживаем, что при движении в сферически-симметричной среде с переменным показателем преломления ${nr\sin \left(\varphi \right)=const\ }$. Применим этот результат к нашей задаче, в которой ${nr\sin \left(\varphi \right)=2Rsin(\alpha )\ }$. Так как угол падения луча на поверхность полости должен быть меньше угла ПВО (${\mathrm{sin} \left[\varphi \left(R\right)\right]\ }<\frac{1}{n(R)}\ )$, и ${n(R)\mathrm{sin} [\varphi \left(R\right)]=2sin(\alpha )\ }$, то $sin\left(\alpha \right)<\frac{1}{2}$, и для попадания внутрь полости угол падения луча на поверхность шара должен удовлетворять условию $\alpha <30{}^\circ $.
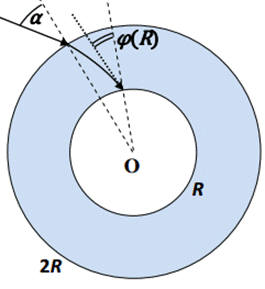
Однако, для того чтобы при таких $\alpha $ луч мог «добраться» до границы полости, необходимо, чтобы световой луч не прошел мимо нее. Заметим, что при проходе мимо полости угол между лучом и радиусом должен в какой-то точке достигнуть значения $\varphi =90{}^\circ $ - тогда $r$ перестает убывать. В этом случае луч либо движется по окружности, либо "разворачивается'' и в конечном итоге покидает слой. Покажем, что в нашем случае это невозможно. Произведение $f\left(r\right)=n\left(r\right)\cdot r=2,5\cdot r-0,5\frac{r^2}{R}$ — квадратный трехчлен с максимумом при $r=2,5R$. В интервале $R < r < 2R$ функция $f\left(r\right)$ всюду возрастает при росте $r$ и, поскольку $f\left(r\right)sin\varphi =C$, то по мере приближения к центру угол $\varphi $ всюду возрастает. Так как конечный угол меньше $\mathrm{arcsin}\left(\frac{1}{2}\right) = 30\mathrm{{}^\circ}<90{}^\circ$, то и при больших значениях радиуса угол не сможет возрасти до $90\mathrm{{}^\circ}$. Итак, при всех $\alpha < 30{}^\circ $ луч достигает границы полости и проникает внутрь (рисунок 4).
Ответ:
При всех $\alpha <30{}^\circ $ луч достигает границы полости и проникает внутрь.