Pho.rs: Анизотропные волноводы

Условие

Edu

Y22

Введение

В последние годы фотонные технологии играют всё большую роль в схемотехнике. Они позволяют достичь больших скоростей и качества передачи и обработки информации. Основным устройством для передачи света является волновод — система из сердцевины, по которой перемещается волна, и оболочки, сдерживающей выход света наружу с помощью эффекта полного внутреннего отражения. К сожалению, при переходе на субдифракционные масштабы возникает новая проблема — в волноводах, размер которых мал по сравнению с длиной волны, излучение становится очень сложно удержать внутри, что приводит к большим потерям мощности и возможному переходу волн между соседними волноводами. В качестве одного из решений такой проблемы предлагается использовать так называемые анизотропные волноводы, которые состоят из полностью прозрачных диэлектрических материалов, в которых наблюдается анизотропия, т.е. связь полей $\vec D$ и $\vec E$ в них записывается в виде:\[D_x=\varepsilon_{x}E_x+\varepsilon_{xy}E_y+\varepsilon_{zx}E_z\\D_y=\varepsilon_{xy}E_x+\varepsilon_{y}E_y+\varepsilon_{yz}E_z\\D_z=\varepsilon_{zx}E_x+\varepsilon_{yz}E_y+\varepsilon_{z}E_z\]

где $\varepsilon_{x}$, $\varepsilon_{y}$, $\varepsilon_{z}$, $\varepsilon_{yz}$, $\varepsilon_{zx}$ и $\varepsilon_{xy}$ — некоторые величины. Как вы увидите далее, иногда это действительно позволяет заметно улучшить характеристики волноводов.

Анизотропные волноводы предлагается изготавливать по следующей технологии. Сердцевина волновода делается из изотропного материала, в этой задаче это кремний $\rm Si$ (его показатель преломления $n_\mathrm{Si}=3.47$, поэтому $\varepsilon=n_\mathrm{Si}^2=12.04$). Для изготовления оболочки анизотропных волноводов предлагается использовать слоистую наноструктуру, показанную на рисунке 1. Оболочка состоит из последовательности чередующихся тонких наноплёнок из двух разных материалов, в этой задаче это германий $\rm Ge$ и диоксид кремния $\rm SiO_2$ (их показатели преломления $n_\mathrm{Ge}=4.3$ и $n_\mathrm{SiO_2}=1.5$ соответственно). Теоретически можно показать, что такая среда обладает анизотропными свойствами. Слоистая структура характеризуется объёмной долей $\rho$ материала с большей диэлектрической проницаемостью, т.е. германия. В системе координат, введённой на рисунке 2, величины $\varepsilon_{yz}$, $\varepsilon_{zx}$ и $\varepsilon_{xy}$ равны нулю, а
\[\begin{cases}\varepsilon_x=\left(\frac{\rho}{
\varepsilon_1}+\frac{1-\rho}{\varepsilon_2}\right)^{-1}\\\varepsilon_z=\varepsilon_1\rho+\varepsilon_2(1-\rho)\end{cases}\]В данном случае $\varepsilon_1=n_\mathrm{Ge}^2=18.49$ и $\varepsilon_2=n_\mathrm{SiO_2}^2=2.25$.

В задаче будем рассматривать волны, распространяющиеся по волноводу вдоль оси $z$ и имеющие только одну отличную от нуля компоненту магнитного поля — $H_y$. Длина волны в вакууме $\lambda_0$ считается фиксированной на протяжении всей задачи, а ширина волновода обозначается как $2a\lambda_0$. Несложно показать, что пространственная амплитуда магнитного поля в такой волне должна иметь вид:\[H_y=\left\{\begin{array}{ll}A\cos\left(kx\right)e^{i\beta z},&|x| < a\lambda_0\\Be^{-k_xx}e^{i\beta z},&|x|\geq a\lambda_0\end{array}\right.\]где $A$ и $B$ — постоянные, определяемые из граничных условий, $k$ и $\beta$ — $x$- и $z$-компоненты волнового вектора в сердцевине волновода, а $k_x$ — мнимая часть $x$-компоненты волнового вектора в оболочке. Для простоты дальнейшей работы введём следующие безразмерные величины: $v\equiv ak\lambda_0$, $w\equiv ak_x\lambda_0$ и $\tilde x\equiv\frac{x}{a\lambda_0}$. Тогда выражение для магнитного поля запишется в виде:\[H_y=\left\{\begin{array}{ll}A\cos\left(v\tilde x\right)e^{i\beta z},&|\tilde x| < 1\\Be^{-w\tilde x}e^{i\beta z},&|\tilde x|\geq1\end{array}\right.\]Отсюда несложно вывести и выражение для $x$-компоненты электрического поля в волноводе:\[E_x=\frac{\beta}{\omega\varepsilon_0}\left\{\begin{array}{ll}\frac A{\varepsilon}\cos\left(v\tilde x\right)e^{i\beta z},&|\tilde x| < 1\\\frac B{\varepsilon_x}e^{-w\tilde x}e^{i\beta z},&|\tilde x|\geq1\end{array}\right.\]где $\omega$ — циклическая частота пропускаемого по волноводу излучения.

Центральной задачей при моделировании волноводов является численное решение уравнений Максвелла. Для рассматриваемого волновода эта задача не представляет собой особой сложности и сводится к нахождению $v$ и $w$ из следующей системы уравнений:\[\begin{cases}w=\frac{\varepsilon_z}{\varepsilon}v\operatorname{tg}v\\v^2+\frac{\varepsilon_x}{\varepsilon_z}w^2=4\pi^2a^2(\varepsilon-\varepsilon_x)\end{cases}\]получаемой из выражений для поля с учётом граничных условий.

Примечание: При решении задачи приводите ответы для $\varepsilon_x$, $\rho$ и $\varepsilon_z$ с точностью два знака после запятой, все остальные величины — с точностью три знака после запятой. При вычислениях сохраняйте достаточную точность, чтобы промежуточное округление не повлияло на финальный результат.

Часть A. Профили поля в волноводе (3.7 балла)

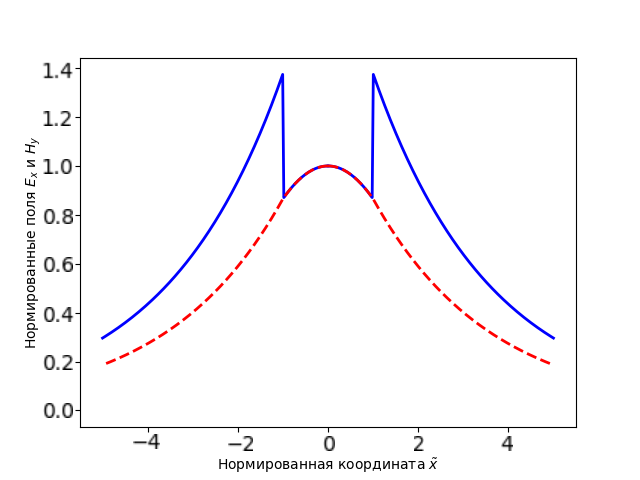
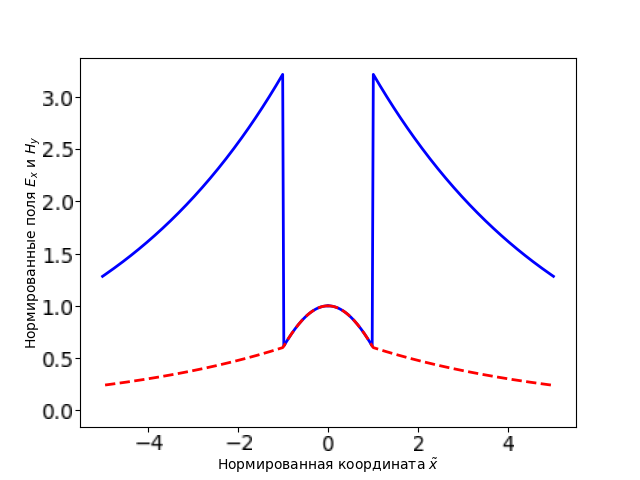
Основной особенностью рассматриваемых анизотропных волноводов является быстрое затухание $x$-компоненты электрического поля. В этой части задачи вам предлагается посчитать некоторые характеристики по профилю $E_x$ для двух различных волноводов одинакового размера. Будем рассматривать профили $E_x$ для двух волноводов с $a=0.1$ и разными значениями $\rho$. В таблице в листе ответов приведены зависимости $x$-компоненты поля от координаты $\tilde x$, нормированные на значение $E_x$ в центре.

A1 ^1.00 Найдите $v$ и $w$ для первого волновода.

A2 ^0.40 Выразите $\varepsilon_x$, $\rho$ и $\varepsilon_z$ через $v$ и $w$. Найдите $\varepsilon_x$, $\rho$ и $\varepsilon_z$ для первого волновода.

A3 ^0.80 Найдите $\varepsilon_x$, $\rho$ и $\varepsilon_z$ ещё одним способом. Сравните полученные результаты. На ваш взгляд, какой из них точнее?

A4 ^1.50 Повторите действия пунктов A1-3 для второго профиля. Что вы можете сказать о втором волноводе?

Часть B. Переносимая мощность (6.3 балла)

Как уже указывалось во введении, нахождение волноводов на малом расстоянии друг от друга может привести к тому, что волна из одного волновода может переместиться в другой. Чтобы такого не происходило, важно, чтобы как можно большая часть мощности переносимого излучения проходила через сердцевину. На больших масштабах анизотропные волноводы проигрывают по этому показателю, однако на малых показывают высокую эффективность по сравнению с обычными. В этой части задачи вам предстоит самостоятельно проверить это утверждение и оценить масштабы, на которых анизотропные волноводы становятся эффективными.

Обозначим мощность, переносимую через единицу поперечной длины сердцевины волновода, как $P_\mathrm{core}$, а аналогичный показатель для всего волновода — как $P_\mathrm{total}$.

B1 ^0.50 Выразите $\frac{P_\mathrm{core}}{P_\mathrm{total}}$ через $v$, $w$, $\varepsilon$ и $\varepsilon_x$.

Подсказка: Плотность потока энергии электромагнитного поля задаётся средним значением вектора Пойнтинга $\langle\vec S\rangle=\left<[\vec E\times\vec H{}^*]\right>$, где ${}^*$ обозначает комплексное сопряжение.

В листе ответов вам дана таблица, в которой содержатся значения $a$, для которых планируется изготовление анизотропных волноводов с $\rho=0.80$ и обычных волноводов (с тем же материалом сердцевины; их оболочка состоит из чистого $\rm SiO_2$).

B2 ^2.25 Для анизотропного волновода найдите $v$, $w$ и $\frac{P_\mathrm{core}}{P_\mathrm{total}}$ для каждого из указанных значений $a$.

В3 ^2.25 Для обычного волновода найдите $v$, $w$ и $\frac{P_\mathrm{core}}{P_\mathrm{total}}$ для каждого из указанных значений $a$.

В4 ^0.90 Постройте на одном листе графики $\frac{P_\mathrm{core}}{P_\mathrm{total}}(a)$ для обычного и анизотропного волноводов.

B5 ^0.20 Найдите, во сколько раз мощность, переносимая сердцевиной анизотропного волновода, превосходит мощность, переносимую сердцевиной обычного, при ширине волновода $a=0.05$.

B6 ^0.20 Оцените, при каком $a_\rm{cr}$ анизотропный волновод начнёт проигрывать обычному по доле переносимой сердцевиной энергии.