В 90-х годах прошлого века была разработана технология, позволяющая создавать и управлять крайне малыми потоками жидкости, заключенными в ограниченном пространстве (характерные размеры меньше миллиметра). Эта технология называется микрофлюидика. С ее помощью, в частности, можно построить лабораторию-на-чипе (lab-on-chip), где в системах капилляров можно смешивать и разделять реагенты, воздействовать на разные части чипа температурой, током и другими параметрами. В итоге это позволяет использовать реагенты в очень малых количествах, что существенно удешевляет процессы разработки, особенно в химии современных лекарств.

Часть А. Течение в капилляре под действием разности давлений (2 балла)

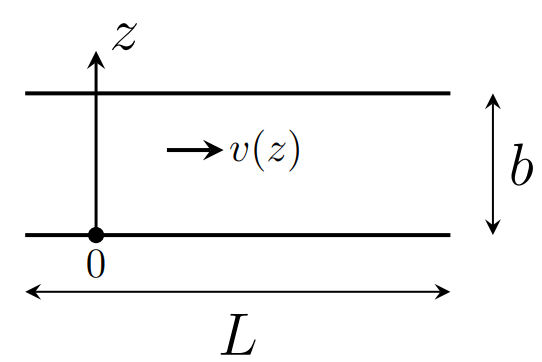
Настоящие капилляры имеют круглое или квадратное/прямоугольное сечение. Однако в этой задаче для простоты расчетов будем рассматривать прямоугольный капилляр с поперечными размерами $a$ и $b$ ($a \gg b$) и длины $L$ ($L \gg a$). Такой капилляр заполнен водой, и к его концам приложена разность давлений $\Delta P$.

A1  ^1.00 Пусть в капилляре имеется установившееся ламинарное течение воды. Найдите зависимость скорости течения жидкости $v(z)$ в капилляре от координаты $z$ при установившемся ламинарном течении воды в капилляре. Ось $z$ направлена вдоль стороны $b$, начало координат находится на одной из стенок капилляра. Выразите ответ через $\Delta P$, параметры капилляра и вязкость жидкости $\eta$.

A2  ^1.00 В некоторый момент в начальное сечение капилляра $AA'$ равномерно впрыскивается реагент. На рисунке жирные горизонтальные линии обозначают стенки капилляра. В листе ответов нарисуйте, где будет находиться реагент через $\tau=5~с$. Для рисунка выберите подходящий масштаб по горизонтальной оси, которая направлена вдоль течения жидкости.

Параметры капилляра: $L = 8~\text{мм}$, $b = 0.2 ~\text{мм}$, разность давлений $\Delta P = 1.5 ~\text{Па}$, $\eta = 8.9 \cdot 10^{-4}~\text{Па} \cdot \text{с} $. Диффузией реагента пренебрегите.

Часть B. Взаимодействие электролита и стенки капилляра (4 балла)

Электролит — вещество, которое проводит электрический ток вследствие диссоциации на ионы, что происходит в растворах. При контакте двух фаз, одна из которых жидкая, возникает двойной электрический слой (ДЭС) — слой ионов, образующийся на поверхности твердого тела в результате адсорбции ионов из раствора, диссоциации поверхностного соединения или ориентирования полярных молекул на границе раздела фаз. Согласно современной теории структуру ДЭС составляют два слоя:

• Слой Гельмгольца или адсорбционный слой, примыкающий непосредственно к межфазной поверхности (неподвижный);
• Слой Гуи или диффузный слой, в котором находятся ионы электролита обоих знаков. 

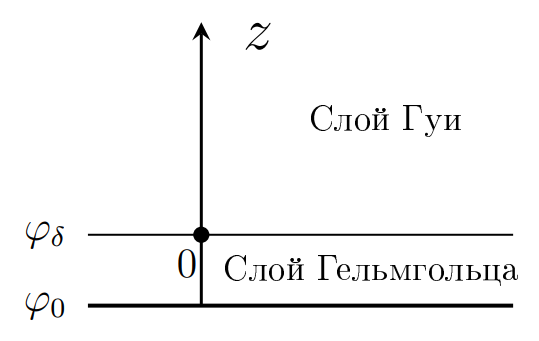
Электрической характеристикой двойного электрического слоя является потенциал, и в этой части задачи нужно найти его характерный вид вблизи одной плоской поверхности стенки капилляра в присутствии электролита. Будем считать, что сам электролит электрически нейтрален, а катионы и анионы имеют заряды $+e$ и $-e$ соответственно. Концентрация ионов каждого из типов вдали от стенок равна $n_0$. Диэлектрическая проницаемость электролита — $\varepsilon$, его вязкость — $\eta$.

Пусть потенциал в объеме электролита равен нулю. Приложим к стенке капилляра некоторый потенциал $\varphi_0$. Из-за эффектов, происходящих в слое Гельмгольца, потенциал на границе этого слоя станет $\varphi_\delta$. Мы не будем в дальнейшем рассматривать процессы, происходящие в слое Гельмгольца, поэтому можно считать, что потенциал у границы капилляра равен $\varphi_\delta$.

Ось $z$ направим перпендикулярно границе капилляра, начало координат находится на границе.

Ионы электролита движутся под действием поля в вязкой среде. Силу сопротивления считайте пропорциональной скорости $\vec f=-\alpha \vec v$.

B1  ^0.50 Найдите установившуюся скорость ионов $v_z(z)$ на расстоянии $z$ от границы капилляра. Считайте, что перемещение иона за время установления скорости мало. Ответ выразите через заряд иона $q$ $(q = \pm e)$, $\alpha$ и потенциал $\varphi(z)$ (и его производные).

В равновесном состоянии поток ионов, вызванный полем, должен быть уравновешен обратным потоком, связанным с разностью концентраций (диффузия), так что полный поток равен нулю. Диффузионный поток описывается законом Фика:
$$
j=-D\cfrac{dn}{dz},
$$
где $j$ — количество частиц, пересекающих единичную площадку в единицу времени, $n$ — концентрация, $D$ — коэффициент диффузии, который для приведенной модели вязкой среды, описывается законом Эйнштейна-Смулоховского $D= kT/\alpha$ ($\alpha$ — тот же коэффициент, что и в силе сопротивления, $k$ — постоянная Больцмана, $T$ — абсолютная температура).

B2  ^1.50 Выразите концентрации катионов ($n_+$) и анионов ($n_-$) вблизи стенки капилляра через потенциал в этой точке, а также через $n_0, e, \alpha, k, T$.

B3  ^0.50 Выразите объемную плотность нескомпенсированного заряда $\rho(z)$ вблизи стенки капилляра через потенциал $\varphi(z)$, концентрацию ионов $n_0$ и физические постоянные $e, k, T$. Считая, что приложенный к стенке потенциал мал ($e\varphi_0 \ll kT$), получите приближенное значение $\rho(z)$.

Во всех следующих пунктах также всегда используйте приближение $e \varphi \ll kT$.

B4  ^1.00 Найдите зависимость потенциала $\varphi(z)$ от координаты вблизи стенки капилляра в диффузном слое. Помните, что на границе потенциал равен $\varphi_\delta$. Выразите ответ через $n_0$, $\varphi_\delta$, $T$, физические постоянные и параметры электролита.

B5  ^0.50 Найдите расстояние $\lambda$ (формулу и численное значение), на котором потенциал $\varphi(z)$ уменьшается в $e$ раз. Эта длина считается характерным размером диффузного слоя Гуи. Вязкость жидкости $\eta = 8.9 \cdot 10^{-4}~\text{Па} \cdot \text{с} $, концентрация ионов $n = 1.1 \cdot 10^{25}~\text{м}^{-3}$, электрическая постоянная $\varepsilon_0 = 8.85 \cdot 10^{-12} ~\text{Ф}/ \text{м}$, постоянная Больцмана $k = 1.38 \cdot 10^{-23}~\text{Дж}/\text{К}$, температура $T = 300~\text{К}$, диэлектрическая проницаемость $\varepsilon = 100$.

Часть С. Движение электролита в капилляре (4 балла)

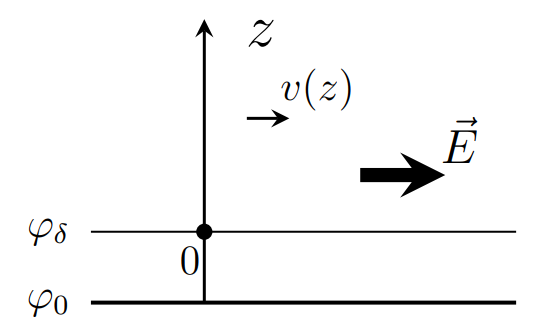
В части B было показано, что вблизи стенки капилляра есть нескомпенсированный объемный заряд. Теперь, если приложить электрическое поле вдоль капилляра, ионы придут в движение, вовлекая за собой и окружающую жидкость. Разумеется, приложенное поле должно быть небольшим, чтобы его вкладом в изменение потенциала $\varphi(z)$ можно было пренебречь.
В этой части не нужно учитывать разность давлений $\Delta P$, о которой говорилось ранее.

C1  ^0.80 Запишите второй закон Ньютона для небольшого объема жидкости в проекции на направление электрического поля, учитывающий вязкое трение и электрическое поле, действующие на нескомпенсированный заряд. Выразите ответ через электрическое поле $E$, концентрацию ионов $n_0$, потенциал $\varphi(z)$, параметры жидкости и капилляра, а также скорость $v(z)$ и ее производные.

C2  ^1.20 Найдите зависимость скорости течения жидкости от координаты $v(z)$.

C3  ^1.00 Пусть в капилляре имеется установившееся ламинарное течение воды. В некоторый момент в сечение $AA'$ капилляра равномерно впрыскивается реагент, рисунок такой же как в части $\mathrm{A}$. В листе ответов нарисуйте, где будет находиться реагент через $\tau=5~с$. Используйте параметры капилляра из $\mathrm{A2}$ и численные данные из $\mathrm{B5}$. Потенциал $\varphi_\delta = 1.8~\text{В}$, падение напряжения на длине капилляра $U = 0.3~\text{В}$. Пренебрегите диффузией реагента вне диффузионного слоя. Для рисунка выберите подходящий масштаб по горизонтальной оси, направленной вдоль направления течения жидкости.

Движение жидкости в микрофлюидике происходит в тонких капиллярах и на небольших скоростях и, таким образом, является как правило ламинарным. В привычных макроскопических трубах перемешивание жидкостей происходит главным образом из-за турбулентных явлений. Соответственно, в микрофлюидике смешивание жидкостей является существенной проблемой.

C4  ^1.00 На основе части $\mathrm{С}$ этой задачи предложите систему, которая позволяет перемешать слои жидкости, текущие вблизи стенки капилляра.