Рассмотрим тонкий слоя жидкости, заключённый между плоскостями с координатами $z_1=z$ и $z_2=z+dz$. Силы вязкого трения, действующие в соответствующих плоскостях:
$$
f_1 = -\eta \ aL \frac{dv_x}{dz} (z) \\
f_2 = \eta \ aL \frac{dv_x}{dz} (z+dz)
$$
Тогда второй закон Ньютона примет вид:
$$
\Delta Pa \ dz + f_1+f_2 = 0 \tag{1}
$$
Отсюда уравнение на скорость:
$$
\frac{d^2v_x}{dz^2} = -\frac{\Delta P}{\eta L} \tag{2}
$$
Заметим, что совершенно необязательно было устремлять толщину слоя к нулю (т.е. уравнение (1) верно и при конечном $dz$). Более того, зафиксировав (например $z_1 =0$ или $z_1 = b/2$), мы получим проинтегрированный аналог уравнения (2).
Общее решение уравнения (2) имеет вид:
$$
v_x = -\frac{\Delta P}{\eta L} \frac{z^2}{2} + C_1 z + C_2
$$
Константы интегрирования определяются граничными условиями, в данном случае — $v(0)=0$ и $v(b)=0$. Отсюда получаем правильный ответ
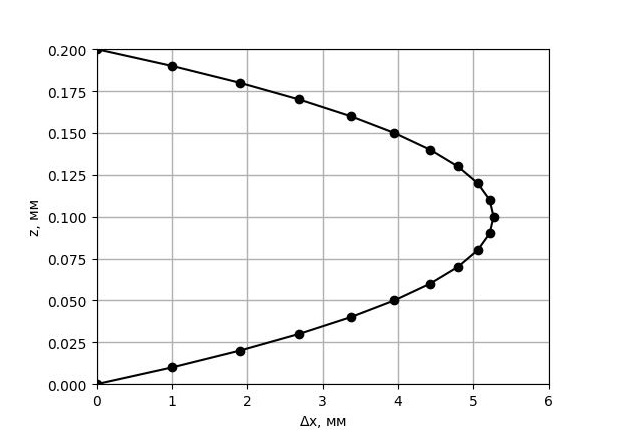
Построим на графике зависимость $x(z) = \tau v(z)$
В установившемся режиме второй закон Ньютона в проекции на ось $z$ выглядит следующим образом:
$$
-\alpha v_z + q E_z = 0
$$
Выражая электрическое поле через градиент потенциала $E_z = - \tfrac{d \varphi}{dz}$, получаем ответ
Поток частиц, связанный с наличием электрического поля уравновешивается потоком ионов, связанным с диффузией. Таким образом, условие баланса будет выглядеть следующим образом:
$$
n v_z -D \frac{dn}{dz} = 0
$$
Подставляя сюда уравнение (3), получим
$$
-\frac{q}{\alpha D} \frac{d \varphi}{dz} = \frac{1}{n} \frac{dn}{dz}
$$
Интегрируя обе части уравнения по $z$ и подставляя $D=\frac{kT}{\alpha}$, находим
$$
-\frac{q}{kT} (\varphi - 0) = \ln(\frac{n}{n_0})
$$
В итоге,
Результат данного пункта является частным случаем распределения Больцмана. Конечно же, такое совпадение не случайно.
$$
\rho = e(n_+ - n_-) = en_0 \left[ \exp \left( -\frac{e \varphi}{kT} \right) - \exp \left( \frac{e \varphi}{kT} \right) \right] = - 2 e n_0 \sinh{\left( \frac{e \varphi}{kT} \right)} \tag{4}
$$
Раскладывая выражение по параметру $\frac{e \varphi}{kT}$, найдём
Теорема Гаусса в дифференциальной форме в одномерном случае имеет вид:
$$
\rho = - \varepsilon \varepsilon_0 \frac{d^2 \varphi}{dz^2}
$$
Используя разложение (5) получаем
$$
\frac{d^2 \varphi}{ dz^2} = 2 \frac{e^2 n_0}{\varepsilon \varepsilon_0 kT} \varphi \tag{6}
$$
Это линейное дифференциальное уравнение, его общее решение в данном случае выглядит следующим образом:
$$
\varphi(z) = C_1 \exp \left( z/\lambda \right) + C_2 \exp \left( - z/\lambda \right),
$$
где $\lambda$ определяется из уравнения (6), а коэффициенты $C_1$ и $C_2$ — из начальных условий $\varphi(0) = \varphi_\delta$ и $\varphi(+\infty) = 0$. Заметим, что второе граничное условие автоматически подразумевает $\lambda \ll b$, т.е. нахождение второй стенки на бесконечности. При учёте отклонения от этого условия, строго говоря, $C_1 \neq 0$. Однако, ответ пункта B5 позволяет отбросить какие-либо сомнения по этому поводу. В итоге
$\textit{Примечание.}$
Заметим более интересный с точки зрения физики момент. Для применимости разложения (5) и характерных значений $\varphi_\delta \sim 1\: В$ температура $T$ должна быть $ T \gg \frac{e \varphi_\delta}{k} \sim 10^4\: \text{К}$!
Однако, используемое в задаче приближение не так плохо, как могло бы показаться на первый взгляд. Убедимся в этом, решив уравнения без использования приближения (5).
Из комбинации (4) и теоремы Гаусса находим:
$$
\frac{d^2 \varphi}{dz^2} = 2 \frac{e n_0}{\varepsilon \varepsilon_0} \sinh{\left( \frac{e \varphi}{kT} \right)}
$$
Далее, интегрируя уравнение по $\varphi$:
$$
\int \sinh{\left( \frac{e \varphi}{kT} \right)} d \varphi = \frac{kT}{e} \cosh{\left( \frac{e \varphi}{kT} \right)} + C
\\
\int \frac{d^2 \varphi}{dz^2} d\varphi = \int \frac{d \varphi'_z}{dz} \varphi'_z \: dz = \int \varphi'_z d \varphi'_z = \frac{ (\varphi'_z)^2}{2} + C,
$$
где $\varphi'_z \equiv \frac{d \varphi}{dz} = - E_z $. Подставляя граничное условие $\varphi'_z (+\infty) = 0$ получаем:
$$
\varphi'_z = -2\sqrt{ \frac{e n_0}{\varepsilon \varepsilon_0} \frac{kT}{e} \left( \cosh{\left( \frac{e \varphi}{kT} \right)} -1 \right)} = -2\sqrt{2\frac{e n_0}{\varepsilon \varepsilon_0} \frac{kT}{e}} \sinh{\left( \frac{e \varphi}{2kT} \right)}
$$
Далее, разделяя переменные и интегрируя:
$$
-2\sqrt{2\frac{e n_0}{\varepsilon \varepsilon_0} \frac{kT}{e}} z = \int \limits_{\varphi_\delta}^\varphi \frac{d \varphi}{\sinh{\left( \frac{e \varphi}{2kT} \right)}} = \frac{2kT}{e} \ln{\tanh{\frac{e \varphi}{4kT}}} \Bigg|_{\varphi_\delta}^\varphi
$$
Отсюда
$$
\varphi = \frac{4kT}{e} \tanh^{-1} \left[ \tanh{ \left( \frac{e \varphi_\delta}{4kT} \right)}{\exp \left(- z/\lambda \right)} \right],
$$
где $\lambda$ в точности равна своему значению в предыдущем рассмотрении.
Теперь проанализируем асимптотику данного решения на бесконечности. Для $z \gg \lambda$ экспонента оказывается малой, поэтому в ведущем приближении $\tanh^{-1} (x) \approx x$, и реальная зависимость оказывается
$$
\varphi \rightarrow \frac{4kT}{e} \tanh{ \left( \frac{e \varphi_\delta}{4kT} \right)}{\exp \left(- z/\lambda \right)}
$$
Такие образом, наше приближение на низких температурах даёт правильное значение \lambda$, однако коэффициент перед экспонентой (префактор) будет неточным.
Потенциал уменьшается в $e$ раз при $z = \lambda$, формула для $\lambda$ была найдена в пункте $B4$.
Данный пункт аналогичен решению пункта $A1$. Силы вязкого трения, действующие на слой будут эквивалентны, а электрическое поле будет действовать с силой
$$
F_E = \rho E\: aL \: dz
$$
Тогда аналогично уравнению $(1)$:
$$
\eta\frac{d^2v}{dz^2} + \rho E = 0
$$
С учетом выражений $(5)$ и $(7)$:
$$
\eta \frac{d^2 v}{dz^2} - \frac{\varepsilon \varepsilon_0 E}{\lambda^2} \varphi_\delta \exp \left( - z/\lambda \right)= 0
$$
Из пункта $C1$ имеем дифференциальное уравнение:
$$
\frac{d^2 v}{dz^2} = \frac{\varepsilon \varepsilon_0 E}{ \eta \lambda^2} \varphi_\delta e^ \left( -z/\lambda \right)
$$
Найдем его решение, проинтегрировав обе части по $dz$ дважды:
$$
v = \frac{\varepsilon \varepsilon_0 E}{ \eta} \varphi_\delta e^ \left( -z/\lambda \right) + C_1z + C_2 \quad (C_1, C_2 = const)
$$
Из граничного условия $v(0) = 0$ находим:
$$
C_2 = -\frac{\varepsilon \varepsilon_0 E}{ \eta} \varphi_\delta
$$
Со вторым граничным условием всё обстоит немного сложнее. Строго говоря, $\textit{правильным}\:$ граничным условием является $v(b)=0$. Однако для того, чтобы рассматривать вторую стенку необходимо внести изменения и в распределение потенциала, добавив возрастающую экспоненту. Но с точки зрения физики это только добавит такую же картинку распределения потенциала у другой стенки.
При рассмотрении же только одной стенки возникает следующая проблема: с используемой точностью при $z \sim \lambda$ любые граничные условия для $z \sim b$ будут неотличимы друг от друга, так как фактически они все эквивалентны бесконечности и члены вида $z/b \ll 1$ пренебрежимо малы. Тем не менее если мы хотим найти распределение потенциала на масштабах размеров трубы, вклад этих членов становится существенным.
В нашей же модели найти $C_2$ можно следующим образом. Обратимся к формуле (8) — она справедлива при любом $\varphi (z)$ . Т.к. граничные условия на стенках одинаковы, $v(z)$ и $\varphi(z)$ должны быть симметричны относительно центра трубы. Из этого факта и формулы (8) следует $C_1 = 0$.
$\textit {Примечание.}$
На самом деле можно получить более общее выражение для скорости $v$, показав, что она зависит только лишь от $\varphi (z)$, при этом вид самой зависимости потенциала от координаты неважен. Запишем уравнение:
$$
\eta\frac{d^2v}{dz^2} + \rho E = 0
$$
С учетом теоремы Гаусса оно запишется в виде:
$$
\eta\frac{d^2v}{dz^2} - \varepsilon \varepsilon_0 \frac{d^2 \varphi}{dz^2} E = 0
$$
Аналогично два раза проинтегрируем по $dz$ и получим:
$$
v =\frac{ \varepsilon \varepsilon_0 E \varphi}{\eta} + C_3 z + C_4 \quad (C_3, C_4 = const)
$$
$C_3 = 0$ в силу симметрии трубки.
При $\varphi = \varphi_\delta$ $v = 0$, откуда $C_4 = -\frac{ \varepsilon \varepsilon_0 E \varphi_\delta}{\eta}$.
Итоговый ответ:
$$
v = \frac{ \varepsilon \varepsilon_0 E}{\eta}(\varphi - \varphi_\delta) \tag{8}
$$
По формуле для скорости, полученной в пункте $C2$ легко рассчитывается смещение слоя жидкости ($\Delta x = v \tau$). Получив значения для нескольких $z$, можно построить график, представленный ниже.
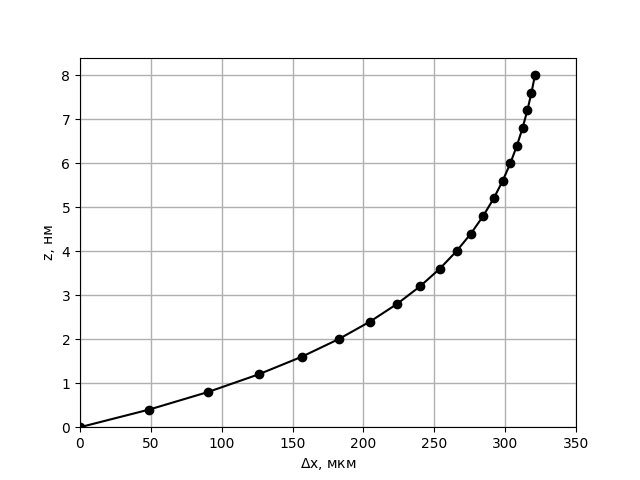
Заметим, что экспонента значительно затухает уже при $z \sim \lambda$. Учитывая, что $\lambda \ll b$, при $z \sim b$ $v \approx -\frac{\varepsilon \varepsilon_0 E}{\eta} \varphi_\delta = const.$, и на рисунке фронт будет изображаться как прямая линия, параллельная оси $z$.