Электрические взаимодействия играют важную роль в живых организмах. Если поместить молекулу кислоты, к примеру, ДНК, в воду, то некоторые слабо связанные с ней атомы могут диссоциировать. Положительные ионы будут покидать молекулу, делая её тем самым отрицательно заряженной. Точно так же и клеточные мембраны в воде будут заряжаться отрицательно, а электростатическое отталкивание между ними предотвращает «слипание» макромолекул, мембран и клеток. Поскольку вещество в целом электрически нейтрально, то большое количество положительных ионов в растворе вызовет ослабление силы взаимодействия между мембранами с расстоянием. При решении задачи считайте, что температура всюду равна комнатной $T$.

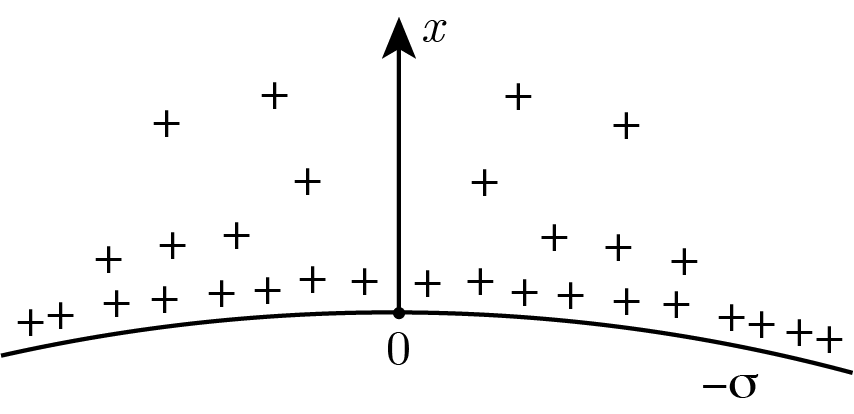
Клеточную мембрану можно считать равномерно заряженной сферой с поверхностной плотностью заряда $(-\sigma)$. В мембрану заключено нейтральное содержимое клетки. Мембрана окружена раствором с диэлектрической проницаемостью $\varepsilon$. Положительные ионы плавают в тонком слое этого раствора вблизи внешней поверхности мембраны. Рассмотрим фрагмент мембраны и прилегающий к нему слой. В этой области считайте поле мембраны однородным. Ось $x$ с началом на мембране направим перпендикулярно ей (см. рис.).

Система находится в тепловом равновесии с окружающей средой. Из-за электростатического взаимодействия плотность положительных ионов в растворе неоднородна, но можно считать, что каждая часть локально находится в равновесии. Поведение положительных ионов при этом аналогично поведению молекул в атмосфере с тем лишь исключением, что на положительные ионы действует электрическое поле, а на молекулы атмосферы — гравитационное. Примем концентрацию положительных ионов $n_0$ у самой поверхности мембраны за неопределённую постоянную. Заряд электрона $-e$, заряд положительного иона $+e$, постоянная Больцмана $k$, электрическая постоянная $\varepsilon_0$.
Силу тяжести и вязкость воды не учитывайте.

A1  ^1.00 Запишите дифференциальное уравнение, которому должен удовлетворять потенциал электрического поля $\varphi$.

$\textit{Подсказка:}$ согласно распределению Больцмана, концентрация $n$ частиц с энергией $E$ пропорциональна $\exp\left(-\frac E{kT}\right)$, где $T$ — абсолютная температура среды.

Потенциал на поверхности клетчатой мембраны выбирается равным нулю.

A2  ^0.30 Запишите граничные условия, которым удовлетворяет потенциал $\varphi$ на поверхности мембраны, т.е найдите $\varphi(0)$, $\displaystyle\frac{d\varphi}{dx}(0)$.

При некоторых условиях решение дифференциального уравнения, полученного в пункте $\textbf{A1}$, удовлетворяющее граничным условиям, полученным в пункте $\textbf{A2}$, можно представить в виде логарифмической функции: $\varphi(x)=A_1\ln(1+B_1x)$.

A3  ^0.80 Определите $n_0$, $A_1$ и $B_1$. Выразите $\varphi(x)$ и $n(x)$ (концентрацию положительных ионов в точке $x$) через $\sigma$, $\varepsilon$, $\varepsilon_0$, $T$, $e$ и $k$.

A4  ^0.40 Покажите, что полученное $n(x)$ гарантирует электрическую нейтральность системы.

A5  ^1.50 В расчете на единицу площади мембраны найдите энергию электрического поля $U_f$ и сумму потенциальных энергий положительных ионов $U_e$ в этом поле.

B1  ^0.80 Определите $A_2$ и $B_2$. Выразите ответ через $T$, $\varepsilon$, $\varepsilon_0$ $e$, $k$ и $n_0$.

B2  ^0.50 Введём величину $\theta=B_2D$.
Из граничных условий на поверхности мембраны получите уравнение, связывающее $\theta$ и $e$, $\sigma$, $D$, $\varepsilon$, $\varepsilon_0$, $k$ и $T$.

B3  ^0.40 Выразите $n_0$ через $D$, $\sigma$, $\varepsilon$, $\varepsilon_0$, $T$, $e$, $k$ и $\theta$.

B4  ^0.50 Найдите разность $\Delta n\equiv n(\pm D)-n_0$ между концентрациями положительных ионов у поверхности двух мембран и посередине между ними. Выразите ответ через $\sigma$, $\varepsilon$, $T$ и $k$.

B5  ^0.50 Покажите, что полученное $n(x)$ гарантирует электрическую нейтральность системы.

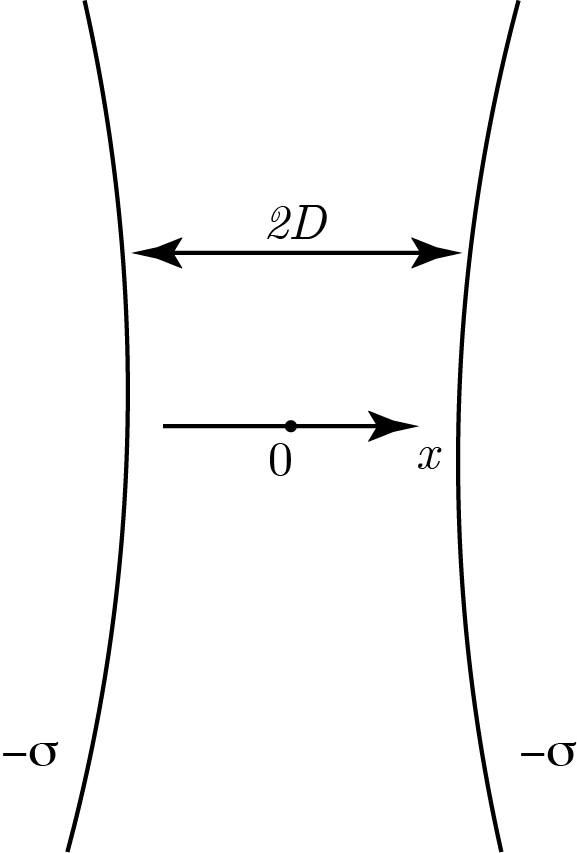
B6  ^1.50 Найдите полную силу $f$, действующую на единицу площади мембраны. Гидростатическим давлением можно пренебречь. Ответ выразите через $e$, $D$, $\theta$, $\varepsilon$, $\varepsilon_0$, $k$ и $T$

$\textit{Подсказка:}$ положительные ионы в воде ведут себя как идеальный газ и локально находятся в тепловом равновесии.

B7  ^1.80 Для сравнительно малых расстояний $D$ зависимость $f(D)$ имеет вид: $f=k_1D^\alpha$, а для больших: $f=k_2D^\beta$. Найдите $\alpha$ и $\beta$.