Часть A. Сила натяжения нити (2 балла)

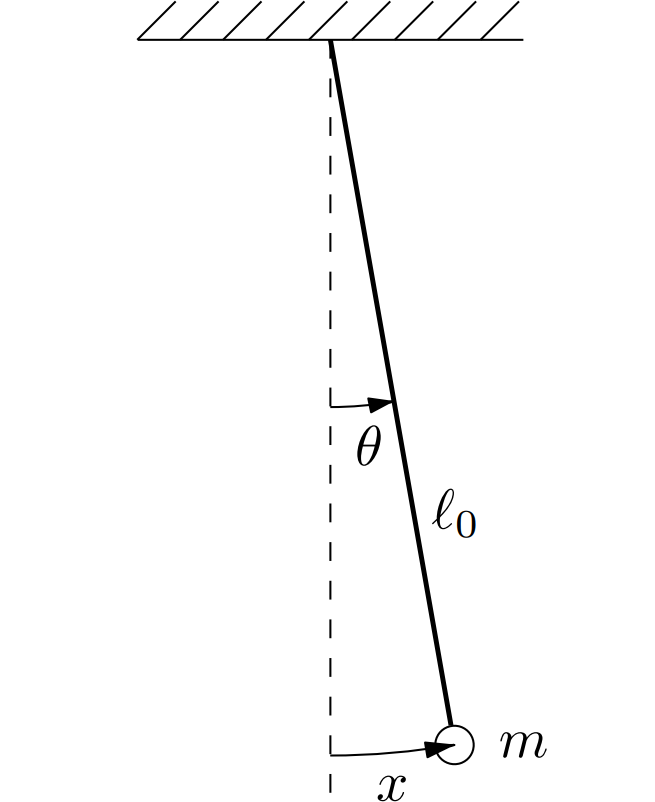
Как показано на рисунке, маятник массой $m$ и длиной $l_0$ может колебаться в вертикальной плоскости. Угол, который он образует с вертикалью, равен $\theta$, а смещение груза по окружности равно $x$ (оба числа положительны при отклонении груза вправо). При $|\theta|\ll1$ можно воспользоваться приближениями $\sin\theta\approx\theta$ и $\cos\theta\approx1-\frac{\theta^2}2$. Нить считайте невесомой и нерастяжимой. Ускорение свободного падения равно $g$.

A1  ^0.40 Запишите уравнение движения маятника.

A2  ^0.40 Выразите $x$ через $\theta$. Пусть амплитуда $\theta$ равна $A$, а в момент времени $t=0$ угол $\theta=0$. Найдите $\theta(t)$.

A3  ^0.30 Найдите зависимость кинетической энергии груза от времени $K(t)$.

A4  ^0.30 Найдите зависимость потенциальной энергии груза от времени $U(t)$.

A5  ^0.10 Найдите полную механическую энергию маятника $E=K+U$. Покажите, что она постоянна.

A6  ^0.50 Натяжение нити $S$ равно сумме центробежной силы и проекции силы тяжести на нить. Покажите, что $S$ можно представить в виде\[S(t)=C_0+C_1\cos(2\omega t),\]где $C_0$, $C_1$ и $\omega$ — положительные постоянные. Выразите $C_0$, $C_1$ и $\omega$ через $m$, $g$, $l_0$ и $A$.

Часть B. Изменение длины маятника (8 баллов)

Предположим теперь, что нить в точке подвеса маятника из части $\bf A$ продета через небольшое отверстие, поэтому её длину можно менять. Рассмотрим, как будет меняться амплитуда колебаний при изменении длины маятника.

B1  ^0.50 При изменении длины маятника необходимо совершить работу. Пусть длина маятника меняется со временем по закону $l(t)$. Найдите, какая для этого нужна мощность. Выразите ответ через $l(t)$ и $S(t)$.

В общем случае при изменении длины нити сила натяжения $S(t)$ отличается от полученной в $\bf A6$. Однако, поскольку в дальнейшем мы будем считать, что $l$ меняется со временем медленно, уравнение из $\bf A6$ можно считать справедливым. Рассмотрим сначала случай, когда скорость относительного изменения $l$ со временем много меньше $\omega$. Для нахождения работы в этом случае можно пренебречь быстро меняющимся членом в уравнении из $\bf A6$.

B2  ^0.50 Найдите работу $\Delta W$, которую необходимо совершить при увеличении длины маятника на $\Delta l$.

При изменении длины нити на $\Delta l$ точка отсчёта потенциальной энергии также смещается вниз на $\Delta l$. Таким образом, определённая в $\bf A5$ энергия маятника должна измениться на $\Delta E$, определённое с учётом изменения нулевого уровня энергии как:\[\Delta E=\Delta W-(-mg\Delta l)=\Delta W+mg\Delta l.\]

B3  ^1.50 При изменении длины нити период $T$ маятника также изменяется и становится равным $T+\Delta T$. Покажите, что в первом приближении справедливо равенство:\[\frac{\Delta E}E+\frac{\Delta T}T=0.\]При $|\delta|\ll1$ можно пользоваться приближением $(1+\delta)^\alpha\approx1+\alpha\delta$.

Поскольку в первом приближении изменение произведения энергии маятника на период $(E+\Delta E)(T+\Delta T)-ET$ равно\[ET\left(\frac{\Delta E}E+\frac{\Delta T}T\right)-ET=ET\left(\frac{\Delta E}E+\frac{\Delta T}T\right),\]произведение $ET$ остаётся постоянным.

B4  ^1.50 Как зависит амплитуда маятника $Al$ от $l$ при медленном изменении длины нити?

Теперь будем считать, что длина нити меняется по следующему закону:\[l(t)=l_0-a\sin(\Omega t).\]Предполагается, что $0 < a\ll l_0$, а $\Omega$ — величина одного порядка с $\omega$.

B5  ^2.50 Теперь вкладом осциллирующего члена в уравнении из $\bf A6$ уже нельзя пренебречь. Найдите, какую работу нужно совершить над маятником в промежутке времени от $0$ до $t$.

B6  ^1.50 Покажите, что при $\Omega=2\omega$ энергия маятника на больших временах увеличивается прямо пропорционально $t$.