Pho.rs: Соленоид и виток

1 ^?? Точки $A$ и $C$ расположены в плоскости витка на расстояниях $r/3$ и $3r$ соответственно от оси симметрии системы.
Найдите проекции индукции $B_{Ax}$ и $B_{Cx}$ магнитного поля, создаваемого соленоидом в точках $A$ и $C$ соответственно.

$$\large{\textbf{Первое решение}}
$$
Добавим к исходному соленоиду такой же, дополнив его до бесконечного.
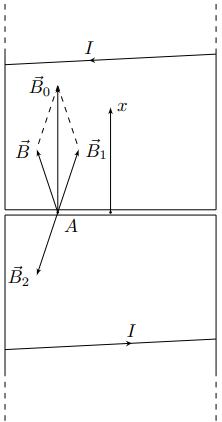
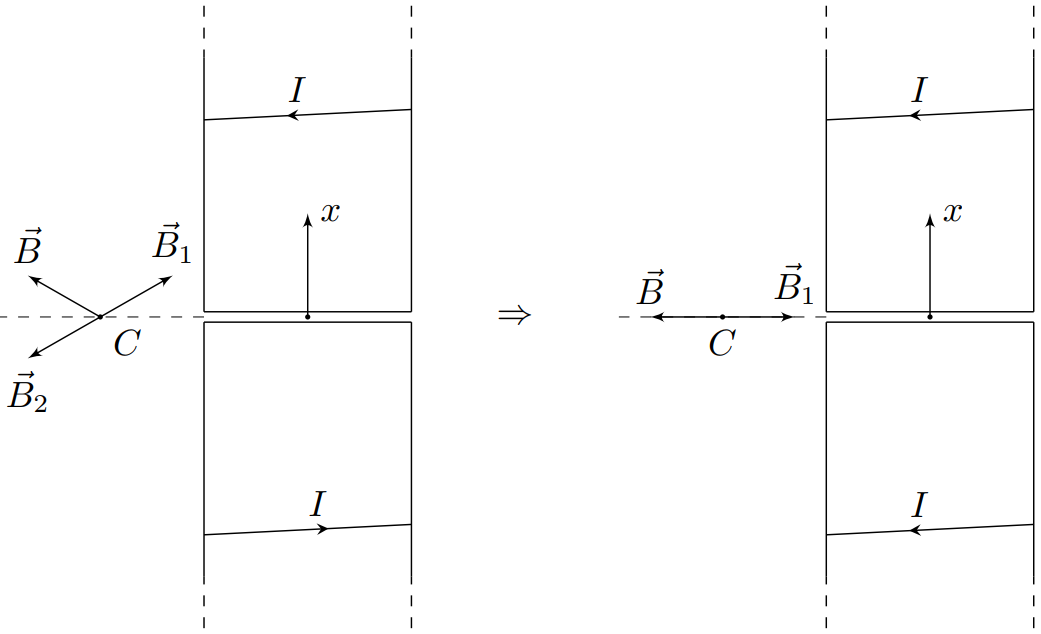
Обозначим магнитные поля исходного и добавленного соленоидов за $\vec{B}$ и $\vec{B}_1$ соответственно.
Если направление силы тока в добавленном соленоиде изменить на противоположное, то и создаваемое им магнитное поле $\vec{B}_2$ изменится на противоположное, т.е $\vec{B}_2=-\vec{B}_1$.
Добавленный соленоид с изменённым на противоположное направлением силы тока симметричен исходному относительно основания, поэтому создаваемые добавленным и исходным соленоидами магнитные поля $\vec{B}_2$ и $\vec{B}$ соответственно будут также симметричны относительно основания.

Рассмотрим в точки, принадлежащие основанию.
На рис.1 показаны исходный соленоид и добавленный с противоположным направлением тока.
Поскольку внутри соленоида магнитное поле $\vec{B}_0$ однородно, имеем:
$$B_x+B_{1x}=B_0{.}
$$
Также, поскольку магнитные поля $\vec{B}$ и $\vec{B}_2$ симметричным относительно основания, имеем:
$$B_x+B_{2x}=0{.}
$$
Комбинируя полученные равенства, находим:
$$B_x=B_{1x}=\displaystyle\frac{B_0}{2}{.}
$$
Таким образом, в исходной ситуации в точке $A$ проекция магнитного поля на ось $x$ равна:

Ответ: $$B_{Ax}=\displaystyle\frac{\mu_0nI}{2}{.}
$$

Рассмотрим в плоскости основания точки, не принадлежащие ему.
Поскольку магнитное поле вне бесконечного соленоида равно нулю:
$$\vec{B}+\vec{B}_1=0{.}
$$
Тогда $\vec{B}_2=-\vec{B}_1=\vec{B}$. Поскольку векторы $\vec{B}$ и $\vec{B}_2$ симметричны относительно основания – в рассматриваемых точках магнитное поле направлено в плоскости основания, иначе $\vec{B}_2\neq{\vec{B}}$ ⃗ (см.рис.2.)
Таким образом, в исходной ситуации в точке $C$ проекция магнитного поля на ось $x$ равна:

Ответ: $$B_{Cx}=0{.}
$$

$$\large{\textbf{Второе решение}}
$$
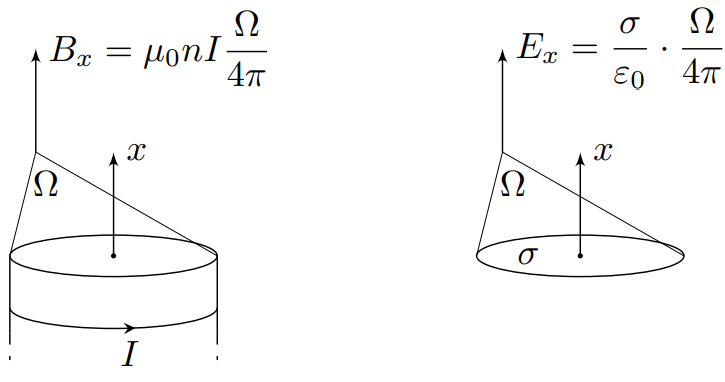
Второй вариант рассуждений может быть построен на использовании теоремы о телесном угле для магнитного поля. Если по плоскому слою течёт ток линейной плотностью $\vec{i}$ , то в точке $O$ компонента магнитного поля, направленная вдоль слоя перпендикулярно $\vec{i}$, равна:
$$B_{O||}=\displaystyle\frac{\mu_0i\Omega_O}{4\pi}{,}
$$
где $\Omega_O$– телесный угол, под которым виден слой из точки $O$.
Применяя теорему о телесном угле к осевой компоненте магнитного поля соленоида, получим:
$$B_x=\displaystyle\frac{\mu_0nI \Omega_\text{бок}}{4\pi}{,}
$$
где $\Omega_\text{бок}$ – телесный угол, под которым видна боковая поверхность соленоида(с учётом знака, данная величина может быть и отрицательна).
Отметим, что утверждения, данные в примечании к условию задачи, могут быть получены с помощью этой теоремы.
В точках, принадлежащих основанию, боковая поверхность соленоида видна под телесным углом $\Omega_\text{бок}=2\pi$, а в точках, лежащих в плоскости основания и не принадлежащих ему, боковая поверхность соленоида видна под нулевым телесным углом. Отсюда получим ответы:

Ответ: $$B_{Ax}=\displaystyle\frac{\mu_0nI}{2}\qquad B_{Cx}=0{.}
$$

2 ^?? Найдите силу тока $I_\text{в}$ в витке. Укажите, как он направлен.

Поскольку виток сверхпроводящий, магнитный поток, пронизывающий его, должен оставаться постоянным и равным нулю. Пусть $\Phi_\text{с}$ – магнитный поток через виток от соленоида. Выберем положительное направление силы тока в витке такое, как и в соленоиде, тогда:
$$\Phi_\text{с}+LI_\text{в}=0{.}
$$
Как было показано в п.1, осевая компонента магнитного поля в плоскости витка на расстояниях меньших $r$ постоянна и равна $\displaystyle\frac{B_0}{2}$, а на расстояниях больших $r$ равна нулю. Поэтому поток магнитного поля соленоида через виток равен $\Phi_\text{с}=\displaystyle\frac{B_0S}{2}$, где $S$ – площадь основания соленоида.
С учетом $S=\pi{r}^2$, находим:
$$\Phi_\text{с}=\displaystyle\frac{\pi\mu_0nIr^2}{2}{,}
$$
и получаем ответ на второй вопрос:

Ответ: $$I_\text{в}=-\displaystyle\frac{\pi\mu_0nIr^2}{2L}
$$
(ток в витке направлен против тока в обмотке соленоида).

3 ^?? Найдите величину и направление силы магнитного взаимодействия, действующей на соленоид со стороны витка.

$$\large{\textbf{Первое решение}}
$$
Сила взаимодействия витка с соленоидом направлена вдоль их общей оси.

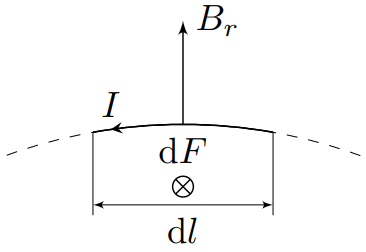
Пусть $B_r$ – компонента магнитного поля витка, направленная перпендикулярно боковой поверхности соленоида. Рассмотрим элемент тока соленоида длины $dl$. Будем искать силу притяжения витка к соленоиду. Осевая компонента силы Ампера, действующей на него, равна:
$$dF_{1x}=-IB_rdl{.}
$$

В толщине слоя $dh$ находится $dN=ndh$ витков, а сила, действующая на них равна:
$$dF_x=dF_{1x}dN=-InB_rdldh{.}
$$
Отметим, что $dldh=dS_\text{бок}$ – элемент площади боковой поверхности соленоида.
Тогда выражение для элемента силы можно переписать в виде:
$$dF_x=-Ind\Phi_\text{бок}{,}
$$
где $\Phi_\text{бок}$ – поток магнитного поля витка через боковую поверхность соленоида.
Равнодействующая сила равна:
$$F_x=-In\Phi_\text{бок}{.}
$$
Для нахождения $\Phi_\text{бок}$ воспользуемся теоремой Гаусса для магнитного поля: через любую замкнутую поверхность поток магнитного поля равен нулю. Тогда имеем:
$$\Phi_\text{бок}+\Phi_\text{осн}=0{,}
$$
где $\Phi_\text{осн}$ – поток магнитного поля витка через основание соленоида.
Поскольку $r\ll{R}$, магнитное поле витка в ближнем основании соленоида можно считать однородным и равным:
$$B_{\text{в}x}=\displaystyle\frac{\mu_0I_\text{в}}{2R}{.}
$$
Также, поскольку соленоид полубесконечный, в дальнем основании соленоида магнитное поле витка равняется нулю.
Тогда для $\Phi_\text{осн}$ имеем:
$$\Phi_\text{осн}=B_{\text{в}x}S=\displaystyle\frac{\mu_0I_\text{в}S}{2R}{,}
$$
откуда находим:

Ответ: $$F_x=-\displaystyle\frac{1}{RL}\left(\displaystyle\frac{\pi\mu_0nIr^2}{2}\right)^2
$$
Соленоид и виток отталкиваются.
$\textit{Примечание:}$ Отметим, что метод решения, использующий силу, действующую на виток с током в неоднородном магнитном поле, эквивалентен решению, описанному выше.

$$\large{\textbf{Второе решение}}
$$
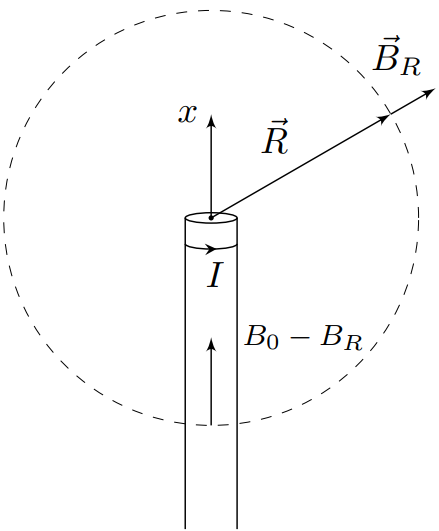
На больших ($R\gg{r}$) расстояниях от основания полубесконечного соленоида источник магнитного потока $\Phi_0=B_0S$ – ближний торец соленоида – выглядит практически точечным, и магнитный поток от него растекается практически равномерно по всем направлениям. Покажем это.

В соответствии с п.1 в основании соленоида проекция на ось $x$ создаваемого им магнитного поля постоянна и равна $B_x=\displaystyle\frac{\mu_0nI}{2}$.
Изменение магнитного поля вне соленоида описывается теоремой Гаусса, а также теоремой о циркуляции для магнитного поля.
Поскольку токи вне соленоида отсутствуют, циркуляция магнитного поля по любому замкнутому контуру, не пересекающему поверхность соленоида, равна нулю.
Теми же уравнениями описывается электрическое поле тонкого диска, заряженного по поверхности с плотностью заряда $\sigma$.
Действительно, проекция на ось $x$ электрического поля диска на его поверхности постоянна и равна $\displaystyle\frac{\sigma}{2\epsilon_0}$.
Поскольку вне диска электрические заряда отсутствуют, поток электрического поля через любую поверхность, не пересекающую плоскость диска, равен нулю. Циркуляция электрического поля по любому замкнутому контуру также равна нулю.

В частности, убедимся в эквивалентности формул для $B_x$ и $E_x$ вне соленоида (рис.5.)

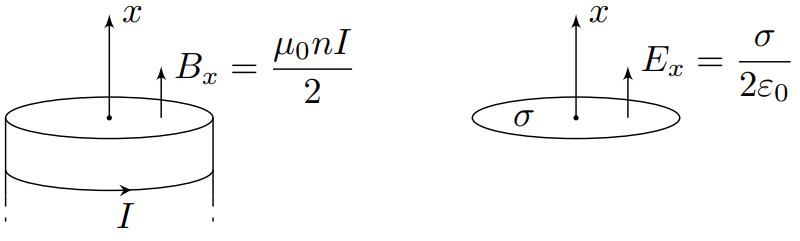
В соответствии с аналогией структур магнитного поля полубесконечного соленоида и электрического поля равномерно заряженного диска, на расстоянии $R\gg{r}$ от основания соленоида магнитное поле соленоида направленно вдоль линии, соединяющей рассматриваемую точку с основанием и равняется:
$$B_R=\displaystyle\frac{\mu_0nIr^2}{4R^2}{.}
$$

Отметим, что изложенный вывод не противоречит теореме Гаусса для магнитного поля. Действительно, из теоремы о телесном угле для магнитного поля следует, что разность проекций магнитного поля внутри и вне соленоида на ось $x$ равна $B_0$. Применяя теорему Гаусса для сферической поверхности радиуса $R\gg{r}$ с центром в центре основания (см.рис.6), получим:
$$4\pi{R}^2B_R=\Phi_0=\pi{r}^2B_0{,}
$$
что совпадает с полученным из аналогии результатом.

Результирующая сила отталкивания, действующая на виток со стороны соленоида, равна:
$$F_{\text{в}x}=-2\pi{R}I_\text{в}B_R=\displaystyle\frac{1}{RL}\left(\displaystyle\frac{\pi\mu_0nIr^2}{2}\right)^2{,}
$$
откуда в соответствии с третьим законом Ньютона получим:

Ответ: $$F_x=-\displaystyle\frac{1}{RL}\left(\displaystyle\frac{\pi\mu_0nIr^2}{2}\right)^2{.}
$$

$$\large{\textbf{Третье решение}}
$$
Задача также допускает энергетическое решение.
Обозначим взаимную индуктивность соленоида и витка за $L_\text{вз}=\displaystyle\frac{\Phi_\text{с}}{I}$.
В рассматриваемом положении она равна $\displaystyle\frac{\mu_0nS}{2}$.
Если обозначить индуктивность соленоида $L_1$, то энергия системы равна
$$E=\displaystyle\frac{L_1I^2}{2}+\displaystyle\frac{LI^2_\text{в}}{2}+L_\text{вз}II_\text{в}{,}
$$
или, с учетом соотношения $L_\text{вз}I+LI_\text{в}=0$:
$$E=\displaystyle\frac{L_1I^2}{2}-\displaystyle\frac{L^2_\text{вз}I^2}{2L}{.}
$$
Изменение энергии системы равняется:
$$dE=-\displaystyle\frac{I^2L_\text{вз}dL_\text{вз}}{L}{.}
$$
При движении соленоида в нём возникает ЭДС индукции. Поскольку сила тока в соленоиде остаётся постоянной, источник, подключенный к соленоиду, компенсирует ЭДС индукции, а значит совершает работу.
Поток магнитного поля витка через соленоид равен
$$\Phi_2=L_\text{вз}I_\text{в}=-\displaystyle\frac{L^2_\text{вз}I}{L}{,}
$$
поэтому работа источника равна:
$$dA_\text{ист}=-\int\limits_0^{t}\mathcal{E}_{инд}Idt=Id\Phi_2=-\displaystyle\frac{2I^2L_\text{вз}dL_\text{вз}}{L}=-2dE{.}
$$
Пусть $F_x$ – сила, действующая на соленоид со стороны витка. Тогда внешняя сила, действующая на соленоид для поддержания его в равновесии равна $-F_x$.
При сдвиге соленоида на $dx$ изменение энергии системы равно
$$dA_\text{ист}-F_xdx=dE{,}
$$
откуда
$$F_x=\displaystyle\frac{dE}{dx}=-\displaystyle\frac{I^2L_\text{вз}}{L}\displaystyle\frac{dL_\text{вз}}{dx}{.}
$$
Найдём изменение взаимной индуктивности $dL_\text{вз}$ при сдвиге соленоида на расстояние $dx$ вдоль оси симметрии. Сдвиг эквивалентен наращиванию еще $dN=ndx$ витков соленоида вблизи торца. Тогда сверхпроводящий виток начинает создавать дополнительный поток $d\Phi_1=B_{\text{в}x}SdN$ через соленоид, а значит, изменение $L_\text{вз}$ составит
$$dL_\text{вз}=d\left(\displaystyle\frac{\Phi_1}{I_\text{в}}\right)=\displaystyle\frac{\mu_0Sndx}{2R}{.}
$$
В последнем выражении мы воспользовались магнитным полем витка в его центре.
Подставляя $L_\text{вз}$ и $dL_\text{вз}$ в выражение для $F_x$, находим:

Ответ: $$F_x=-\displaystyle\frac{1}{RL}\left(\displaystyle\frac{\pi\mu_0nIr^2}{2}\right)^2{.}
$$

$$\large{\textbf{Четвёртое решение}}
$$
Поиск работы источника можно обойти, замкнув подводящие к соленоиду провода накоротко. Тогда поток магнитного поля $\Phi=\left(L_1-\displaystyle\frac{L^2_\text{вз}}{L}\right)I$, пронизывающего соленоид, сохраняется при его перемещении.
Для энергии магнитного поля получим:
$$E=\displaystyle\frac{\Phi^2}{2\left(L_1-\displaystyle\frac{L^2_\text{вз}}{L}\right)}{.}
$$
При перемещении соленоида изменение энергии системы равняется
$$dE=\frac{\Phi^2}{\left(L_1-\displaystyle\frac{L^2_\text{вз}}{L}\right)^2}\frac{L_\text{вз}dL_\text{вз}}{L}=\displaystyle\frac{I^2L_\text{вз}dL_\text{вз}}{L}{.}
$$
Тогда для силы, действующей на соленоид со стороны витка, получим:
$$F_x=-\displaystyle\frac{dE}{dx}=-\displaystyle\frac{I^2L_\text{вз}}{L}\cfrac{dL_\text{вз}}{dx}{.}
$$
Подставляя $L_\text{вз}$ и $dL_\text{вз}$ (см. третье решение) в выражение для $F_x$, находим:

Ответ: $$F_x=-\displaystyle\frac{1}{RL}\left(\displaystyle\frac{\pi\mu_0nIr^2}{2}\right)^2{.}
$$

Соленоид и виток

Решение