A1  ^1.60 Избыточное давление $\Delta P_{\rm s}$ и скачок скорости $\Delta v$ связаны следующим образом: $\Delta P_{\rm s} = \alpha \rho_0 c \Delta v$. Скорость распространения $c$ представима в виде $c = \beta + \sqrt{\gamma B/\rho_0}$.

Найдите $\alpha, \beta$ и $\gamma$.

A1. 1 Выражение для импульса силы	0.10
A1. 2 Выражение для изменения импульса	0.10
A1. 3 Приравнивание импульса силы и изменения импульса	0.10
A1. 4 Верное уравнение непрерывности для сжимаемой жидкости $\rho_{0}\left(c+v_{0}\right)=\rho_{1}\left(c+v_{1}\right)$	0.20
A1. 5 $\alpha < 0$	0.20
A1. 6 M1 $|\alpha|=1+v_{0} / c$	0.30
A1. 7 M2 $|\alpha| \approx 1$	0.10
A1. 8 $\Delta \rho / \rho_{0}=-\Delta V / V_{0}$	0.10
A1. 9 $\beta < 0$	0.10
A1. 10 $|\beta|=v_{0}$	0.20
A1. 11 $\gamma=\left(1+\Delta P_{\mathrm{s}} / B\right)$	0.20
A1. 12 $|\gamma| \approx 1$ либо этот пункт, либо предыдущий	0.10

A2  ^0.60 Рассчитайте $c$ и $\Delta P_s$, если параметры течения воды следующие: $v_0=4.0~{\rm м/с}$ и $v_1 = 0$.

A2. 1 $c=1.5 \times 10^{3}~м/с$	0.20
A2. 2 Единицы измерения скорости	0.10
A2. 3 $\Delta P_{\mathrm{s}}=5.9~МПа$	0.20
A2. 4 Единицы измерения давления	0.10
A2. 5 Верное по порядку $c$	0.10
A2. 6 Верное по порядку $\Delta P_s$	0.10

B1  ^1.00 Найдите избыточное давление $\Delta P_{\rm in} =P_{\rm in}-P_{\rm a}$ на входе в клапан, где линии тока параллельны. Ответ выразите через $\rho_0$, $v_{\rm in}$, $r$, $R$ и $C_c$.

B1. 1 Запись уравнения Бернулли для входного отверстия и места сужения струи $\frac{1}{2} \rho_{0} v_{\mathrm{in}}^{2}+P_{\mathrm{in}}=\frac{1}{2} \rho_{0} v_{\mathrm{c}}^{2}+P_{\mathrm{a}}$	0.20
B1. 2 Верное выражение непрерывности для несжимаемой жидкости $\pi R^{2} v_{\mathrm{in}}=\pi r_{\mathrm{c}}^{2} v_{\mathrm{c}}$	0.10
B1. 3 $r_{\mathrm{c}}^{2}=r^{2} C_{\mathrm{c}}$	0.10
B1. 4 $v_{\mathrm{c}}=\frac{1}{C_{\mathrm{c}}}\left(\frac{R}{r}\right)^{2} v_{\mathrm{in}}$	0.10
B1. 5 M1 $\Delta P_{\text {in }}=P_{\text {in }}-P_{\mathrm{a}}=\frac{1}{2} \rho_{0} v_{\text {in }}^{2}\left[\frac{1}{C_{\mathrm{c}}^{2}}\left(\frac{R}{r}\right)^{4}-1\right]=\frac{k}{2} \rho_{0} v_{\text {in }}^{2}$	0.50
B1. 6 M2 $\Delta P_{\text {in }} \propto v_{\text {in }}^{2}$	0.20

C1  ^0.60 Найдите давление $P_0$ и скорость $v_0$ установившегося потока в трубе, когда клапан $\rm T$ полностью открыт ($r=R$) (см. рис. 1 и 2). Ответ выразите через $\rho_0, g, h$ и $P_{\rm a}$.

C1. 1 Уравнение Бернулли	0.10
C1. 2 Уравнение непрерывности	0.10
C1. 3 $C_{\mathrm{c}}(r=R)=1.0$	0.10
C1. 4 $v_{0}=\sqrt{2 g h}$	0.10
C1. 5 $P_{0}=P_{\mathrm{a}}$	0.20

C2  ^1.20 Рассмотрим установившийся поток, описанный в пункте C1 (давление $P_0$ и скорость $v_0$). Затем в $t=0$ клапан мгновенно перекрывают ($r = 0$). Волна давления распространяется к резервуару со скоростью $c$. Давление $P_h=P_0+\rho_0gh$. Пусть $\tau =2L/c$. Чему равны давления $P(t)$ и скорости потока $v(t)$ в трубе, когда $t$ очень близко к $\tau/2$ и $\tau$?

C2. 1 $P(\tau / 2)=P_{0}+\rho_{0} c v_{0}$	0.30
C2. 2 Частичный балл за $P(\tau / 2)=\rho_{0} c v_{0}$	0.10
C2. 3 $v(\tau / 2)=0$	0.30
C2. 4 $P(\tau)=P_{0}+\rho_{0} g h=P_{h}$	0.30
C2. 5 Частичный балл за $P(\tau)=P_{0}$	0.10
C2. 6 $v(\tau)=-v_{0}+g h / c$	0.30
C2. 7 Частичный балл за $v(\tau)=-v_{0}$	0.10

D1  ^3.00 Выразите $\Delta P_n/(\rho_0 c)$ через $\Delta P_{n-1}/(\rho_0 c)$, $v_{n-1}$ и $v_n$. Выражение должно быть справедливо для всех $n>0$, приведенных в таблице 2.

Для $n=1,2,3$ получите также выражение для расчета $v_n$, если $v_{n-1}$ и $\Delta P_{n-1}/(\rho_0 c)$ известны.

D1. 1 $h=0$ для упрощения уравнений	0.20
D1. 2 $\Delta P=\mp \rho_{0} c \Delta v$ для волн, распространяющихся вдоль направлений $\mp x$	0.20
D1. 3 Изменение знака $\Delta P$ при отражении от конца у резервуара	0.20
D1. 4 Нет изменения знака $\Delta v$ при отражении от конца у резервуара	0.20
D1. 5 Нет изменения знака $\Delta P$ при отражении от конца у клапана	0.20
D1. 6 Изменение знака $\Delta v$ при отражении от конца у клапана	0.20
D1. 7 $\frac{\Delta P_{n}}{\rho_{0} c}=-\left(v_{n}-v_{n-1}\right)-\frac{\Delta P_{n-1}}{\rho_{0} c}$	1.00
D1. 8 Использование $\Delta P_{n}=\frac{1}{2} k_{n} \rho_{0} v_{n}^{2}$, чтобы избавиться от $\Delta P_n$ в рекуррентной формуле	0.40
D1. 9 $\frac{v_{n}}{c}=\frac{-1+\sqrt{1+2 k_{n}\left(\frac{v_{n-1}}{c}-\frac{\Delta P_{n-1}}{\rho c^{2}}\right)}}{k_{n}}$	0.20

D2  ^2.00 Используйте результаты пункта D1 для потока, движущегося со скоростью $v_0=4.0~{\rm м/с}$.

На миллиметровке в листах ответов постройте график зависимости $\Delta P$ от $\rho_0cv$. Точки пересечения ваших отрезков и участков кривых должны давать координаты $\rho_0cv_n$ и $\Delta P_n$ для $n=1,2,3,4$.

Подпишите точки пересечения $(\rho_0cv_n,\Delta P_n)$ для всех $n$.

Из графика оцените значения $\rho_0cv_n$ и $\Delta P_n$ (все в МПа) для $n=1,2,3,4$.

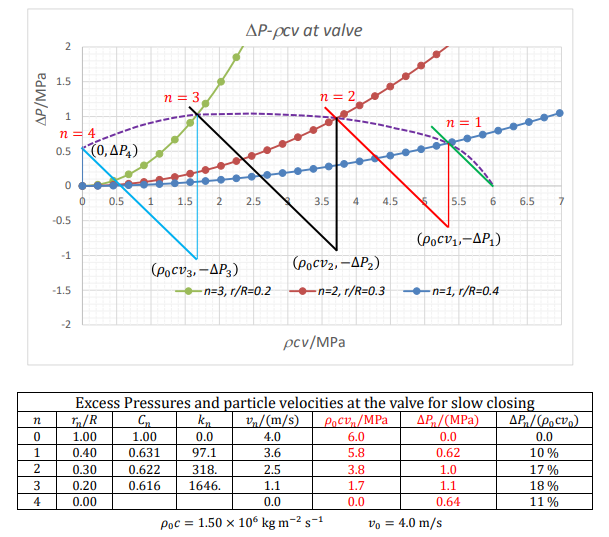
D2. 1	None
D2. 2 Каждый отрезок прямой на графике $\Delta P_{n}(\rho_{0} c v_{n})$, проходящий через $\left(\rho_{0} c v_{n-1},-\Delta P_{n-1}\right)$, с угловым коэффициентом $=-1$	4 × 0.10
D2. 3 Отрезки парабол на графике $\Delta P_{n}(v_{n})$ для $n=1,2,3$	3 × 0.10
D2. 4 Начало в $\rho_{0} c v_{0}=6.0~МПа, \Delta P_{0}=0$	0.10
D2. 5 Конец в $v_4=0$	0.10
D2. 6 Каждая отметка $n$ на графике в точках $\left(\rho_{0} c v_{n}, \Delta P_{n}\right)$	4 × 0.10
D2. 7 Каждая оценка $\Delta P_n$	4 × 0.10
D2. 8 Каждая оценка $\rho_0 cv_n$	3 × 0.10