Конденсатор емкости $C$ соединен последовательно с резистором $R$. На эту систему подается переменное напряжение $V(t)$. Из-за этого на конденсаторе возникает напряжение $U(t)$, которое измеряется идеальным вольтметром. Мы будем исследовать зависимость напряжения на конденсаторе и тока через резистор $I(t)$ от времени в различных режимах. Полярность подключения источника указана на схеме, используйте ее, чтобы указать правильный знак напряжения. Условие задачи содержит подробное объяснение того, как нужно исследовать напряжение на конденсаторе. Важно в каждом пункте задачи находить именно то, что в нем спрашивается. Если нет промежуточных пунктов, баллы за них не ставятся даже при наличии правильного окончательного ответа, полученного другим способом.

Часть A. Постоянное напряжение (2 балла)

A1  ^0.30 Изначально заряд конденсатора равен нулю. Пусть в момент времени $t = 0$ на вход цепи подается постоянное напряжение $V = V_0$. Найдите зависимость напряжения на конденсаторе от времени $U(t)$ при $t > 0$.

A2  ^0.20 Найдите зависимость тока через резистор от времени $I(t)$ ($t > 0$).

A3  ^0.20 Найдите тепло $Q_0$, которое выделится на резисторе за все время процесса.

A4  ^0.60 Пусть теперь начальное напряжение на конденсаторе при $t = 0$ равно $U_1$, и как и раньше на вход подается постоянное напряжение $V = V_0$. Найдите зависимость напряжения на конденсаторе от времени $U(t)$ и тока через резистор $I(t)$.

A5  ^0.70 Найдите количество теплоты $Q_1$, которое выделится за все время процесса из пункта \textbf{A4}. Постройте (качественно) график зависимости $Q_1$ от $U_1$.

Часть B. Линейный рост (4.5 балла)

Пусть теперь на схему подается линейно растущее напряжение $V = \alpha t$ (при $t > 0$). При $t = 0$ конденсатор не заражен. Можно показать, что тогда через достаточно большое время напряжение на конденсаторе будет примерно равно напряжению на входе схемы.

B1  ^0.30 Пусть прошло достаточно большое время. Найдите выражение для тока через резистор $I(t)$.

B2  ^0.20 Найдите количество теплоты $Q$, которое выделится на резисторе за достаточно большое время $t$.

Теперь будем решать задачу точно.

B3  ^0.10 Найдите ток через резистор $I$. Выразите его через мгновенное значение напряжения на конденсаторе $U$, входное напряжение $V$ и параметры схемы.

B4  ^0.10 Выразите скорость изменения напряжения на конденсаторе $dU/dt$ через ток через резистор $I$ и параметры схемы.

B5  ^0.40 Продифференцировав уравнение из \textbf{B3}, получите дифференциальное уравнение на ток через резистор, то есть выразите $dI/dt$ через $I$, параметры схемы и постоянную $\alpha$.

B6  ^0.10 Чему равен ток через резистор в начальный момент времени $I(0)$?

Полученное уравнение для тока выглядит точно так же (с точностью до обозначений), как и уравнение для напряжения на конденсаторе, который заряжается постоянным напряжением.

B7  ^0.50 Используя аналогию с зарядкой конденсатора, найдите зависимость тока через резистор от времени $I(t)$.

B8  ^0.70 Найдите зависимость напряжения на конденсаторе от времени $U(t)$. Постройте (качественно) график зависимости напряжения от времени.

B9  ^0.50 Найдите количество тепла $Q(t)$, которое выделится на резисторе за время $t$.

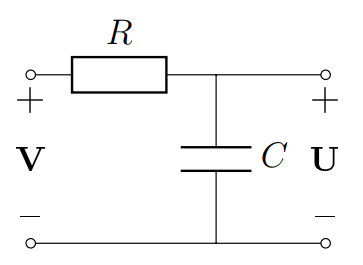
Пусть теперь входное напряжение сначала линейно растет со временем (при $0 < t < T$) до некоторого максимального значения $V_0$, а затем остается постоянным (см. график). Как и раньше, в начальный момент времени $t = 0$ конденсатор не заряжен. Зависимость от времени при $t < T$ мы уже проанализировали. До конца этой части выражайте ответы через параметры схемы, время $t$, $T$ и $V_0$.

B10  ^0.30 Найдите зависимость напряжения на конденсаторе от времени при $t > T$.

B11  ^0.30 Найдите количество тепла $Q_2$, которое выделилось на резисторе при $t > T$.

B12  ^0.40 Найдите количество теплоты $Q_T$, которое выделилось на резисторе за все время зарядки конденсатора.

B13  ^0.60 Найдите отношение $k = Q_T/Q_0$. Здесь $Q_0$ – тепло, которое выделяется на резисторе, когда на вход схемы мгновенно подается напряжение $V_0$ (см. пункт \textbf{A3}), $Q_T$ определено в предыдущем пункте. Запишите приближенное выражение для $k$ при $T \gg RC$.

Часть С. Периодическое напряжение (3.5 балла)

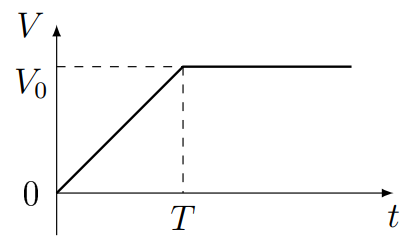
Пусть теперь на конденсатор подается переменное напряжение в виде <<пилы>> (см. график). Это означает, что сначала напряжение на входе нарастает по линейному закону до некоторого максимального значения $V_0$, а затем линейно убывает с той же скоростью, пока не достигнет значения $-V_0$. Далее процесс повторяется периодически с периодом $T$. Через достаточно большое время процесс установится, то есть изменение напряжения на конденсаторе тоже станет периодическим. Пусть в момент времени, когда входное напряжение максимально и равно $V_0$, напряжение на конденсаторе равно $U_1$. В момент, когда напряжение на входе $-V_0$, напряжение на конденсаторе $U_2$.

С1  ^0.20 Пусть прошло достаточно большое время и колебания установились. Как при этом должны быть связаны $U_1$ и $U_2$?

С2  ^0.20 Чему равен ток через резистор $I_1$, когда напряжение на входе равно $V_0$?

С3  ^0.40 По аналогии с пунктом \textbf{B4} напишите уравнение, которому удовлетворяет ток через резистор на участке, где входное напряжение линейно затухает.

C4  ^0.50 С учетом предыдущих двух пунктов найдите зависимость тока от времени на участке, где входное напряжение линейно затухает. Для простоты записи считайте, что этот участок начинается в момент времени $t = 0$.

C5  ^0.60 Используя найденное выражение для тока, выразите напряжение на конденсаторе в конце линейного участка $U_2$ через напряжение в начале $U_1$ и параметры задачи.

С6  ^1.00 Найдите максимальное напряжение на конденсаторе $U_1$ в установившемся режиме. Напишите приближенные выражения для $U_1$ при $T \ll RC$ и $T \gg RC$.

C7  ^0.60 Постройте график зависимости отношения $U_1/V_0$ от безразмерной переменной $T/RC$.