
(1) Градиент функции координат $f(\vec{r})$, $\vec{\nabla}f(\vec{r})$, задается в компонентах
$\vec{\nabla}f \equiv (\hat{x}\frac{\partial}{\partial x}+\hat{y}\frac{\partial}{\partial y}+\hat{z}\frac{\partial}{\partial z})f(\vec{r})$, где $\frac{\partial}{\partial x}f(\vec{r})$ обозначает частную производную $f(\vec{r})$ по $x$ при постоянных $y$ и $z$ . Здесь $\hat{x}$ — единичный вектор вдоль оси $x$, для других осей аналогично.
(2) Интеграл:
$$\int_{0}^{\infty}\,dt\,\frac{(a+pt)}{[(a+pt)^{2}+(b+qt)^{2}]^{3/2}}=\frac{1}{bp-aq}(\frac{b}{\sqrt{a^{2}+b^{2}}}-\frac{q}{\sqrt{p^{2}+q^{2}}}).$$
Мы будем изучать движение маленького магнитного диполя рядом с тонкой проводящей пленкой. В этой задаче под диполем и монополем мы будем понимать магнитный диполь и магнитный монополь соответственно.
Диполь представляет собой сферический постоянный магнит с постоянной намагниченностью $\vec{M}$ (магнитный момент единицы объема вещества) и постоянной плотностью $\rho_{0}$. Его можно рассматривать как точечный при условии, что его радиус $R$ мал. Дипольное приближение хорошо описывает магнитное поле, создаваемое везде вне магнита. Также дипольное приближение хорошо описывает силу, действующую на диполь со стороны внешнего магнитного поля, если расстояние до источников поля много больше $R$.
Точечный диполь можно рассматривать как пару монополей с отрицательным и положительным магнитными зарядами $-q_{\rm m}$ и $q_{\rm m}$ соответственно. Эта пара находится на бесконечно малом расстоянии друг от друга, но обладает конечным дипольным моментом $\vec{m}=q_{\rm m}\vec{\delta}_{\rm m}$. Здесь $\vec{\delta_{\rm m}}$ — вектор, направленный от южного монополя $(-q_{\rm m})$ к северному монополю $(+q_{\rm m})$.
Магнитное поле $\vec{B}_{\rm mp}$ создаваемое монополем $q_{\rm m}$ задается законом, аналогичным закону Кулона
$$\vec{B}_{\rm mp}=\frac{\mu_{0}q_{\rm m}}{4\pi r^{2}}\,\hat{r},$$
где $\vec{r}$ — радиус-вектор, направленный от монополя $q_{\rm m}$ к точке, в которой наблюдается поле, $\hat{r}$ — единичный вектор$\hat{r}=\vec{r}/r$, а $\mu_{0}$ — магнитная постоянная. Приложенное магнитное поле $\vec{B}'$ действует на монополь $q_{\rm m}$ с силой $\vec{F}=q_{\rm m}\vec{B}'$. Магнитное поле монополя можно получить из скалярного потенциала $\Phi$, оно задается формулой $\vec{B}=-\vec{\nabla}\Phi$. Скалярный потенциал $\Phi$ также называется магнитным потенциалом.
Тонкая проводящая пленка имеет постоянную толщину $d$ в направлении $z$ (Рис. 1). Она расположена горизонтально и продолжается вдоль направлений $x$ и $y$ до бесконечности. Ее верхняя поверхность находится на расстоянии $h$ от точечного монополя или диполя. Мы будем рассматривать только случай $h\gg d$. Поэтому можно считать, что объемная плотность индукционного тока в пленке не зависит от $z$. Токами смещения можно пренебречь.
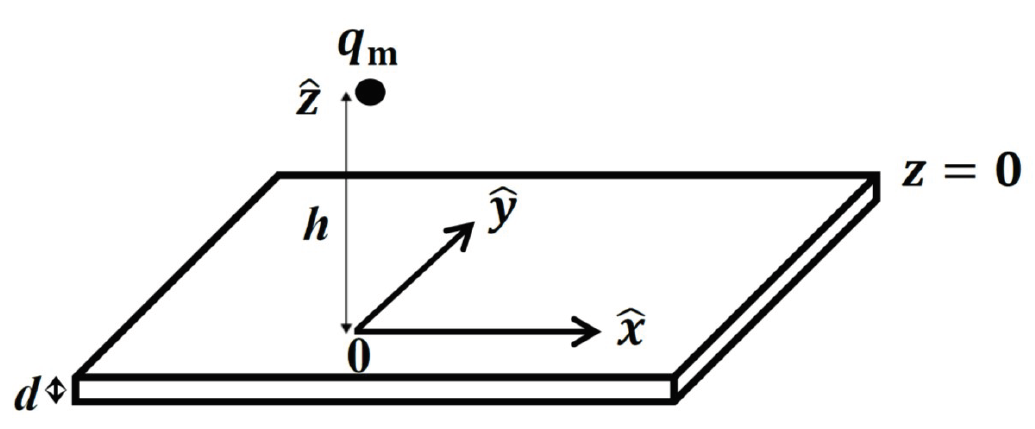
В задаче 3 части. В Части A система состоит из монополя и тонкой пленки, а в Частях B и C из движущегося диполя и тонкой пленки.
Плоскость $z=0$ совпадает с верхней поверхностью тонкой пленки. Вектор $\vec{\rho}=x\hat{x}+y\hat{y}=\rho\hat{\rho}$ — радиус вектор точки в плоскости.
Рассмотрим отклик тонкой проводящей пленки, когда в момент времени $t=0$ северный монополь $q_{\rm m}$ внезапно появляется в точке $\vec{r}_{\rm mp}=h\hat{z}\,\,\,(h>0)$, как показано на Рис. 1. В дальнейшем монополь остается неподвижным ($t>0$).
Вам нужно будет найти начальное полное магнитное поле $\vec{B}(\vec{\rho},z)$ в областях $z\ge 0$ и $z\le -d$, и плотность индуцированного тока в тонкой пленке. Полное магнитное поле $\vec{B}=\vec{B}_{\rm mp}+\vec{B}'$, где магнитные поля $\vec{B}_{\rm mp}$ и $\vec{B}'$ создаются соответственно монополем и индуцированным током в пленке. Начальное поле $\vec{B}(\vec{\rho},z)$ существует в момент времени $t_{0}$, которое лежит в интервале $h/c\le t_{0}\ll\tau_{\rm c}$. Здесь $\tau_{\rm c}$ — характерное время, за которое меняется распределение тока в пленке, а $c$ — скорость света в вакууме. В этой задаче мы рассматриваем предел $h/c\rightarrow 0$ и считаем $t_{0}=0$.
Вычисление начального магнитного поля $\vec{B}(\vec{\rho},z)$ (при $t_{0}=0$) упрощается, если ввести изображение монополя. Для $\vec{B}(\vec{\rho},z)$ в области $z\ge 0$, изображение монополя имеет магнитный заряд $q_{\rm m}$ и расположено в точке $z=-h$. С другой стороны, для $\vec{B}(\vec{\rho},z)$ в области
$z\le -d$ , изображение магнитного монополя имеет заряд $-q_{\rm m}$ и расположено в точке $z=h$.
При $t>0$, полное магнитное поле $\vec{B}$ по принципу суперпозиции становится равным $\vec{B}(\vec{\rho},z;t)=\vec{B}_{\rm mp}(\vec{\rho},z)+\vec{B}'(\vec{\rho},z;t)$, где $\vec{B}'(\vec{\rho},z;t)$ создается индукционным током в тонкой пленке. Вам нужно получить уравнение на $B_{z}'(\rho,z;t)$ рядом с поверхностью $z=0$ тонкой пленки. Зависимость $B_{z}'$ от времени покажет, что поле $\vec{B}'$ рядом с поверхностью $z\approx 0$ при $t>0$ можно получить, считая, что изображение монополя движется.
Уравнение для $B_{z}'$ внутри тонкой пленки приведено ниже,
$$\frac{\partial^{2}B_{z}'(\rho,z;t)}{\partial z^{2}}=\mu_{0}\sigma\frac{\partial B_{z}'(\rho,z;t)}{\partial t}.$$
Это уравнение было получено с помощью уравнений Максвелла для области внутри пленки, а также из закона Ома ($\vec{j}=\sigma \vec{E}$, где $\sigma$ — удельная проводимость), но без учета эффектов тока смещения. В левой части уравнения (2) мы пренебрегли членом $\frac{1}{\rho}\frac{\partial}{\partial\rho}(\rho\frac{\partial B_{z}'}{\partial\rho})$, с учетом условия $h\gg d$.
Идею движущегося изображения монополя, рассмотренная в A.7 для $B_{z}'$ в области $z\approx 0$ можно применить для вычисления поля $\vec{B}'$ во всей области $z\geq 0$. Это предположение годится при условии, что изменение тока в проводящей пленке достаточно медленное.
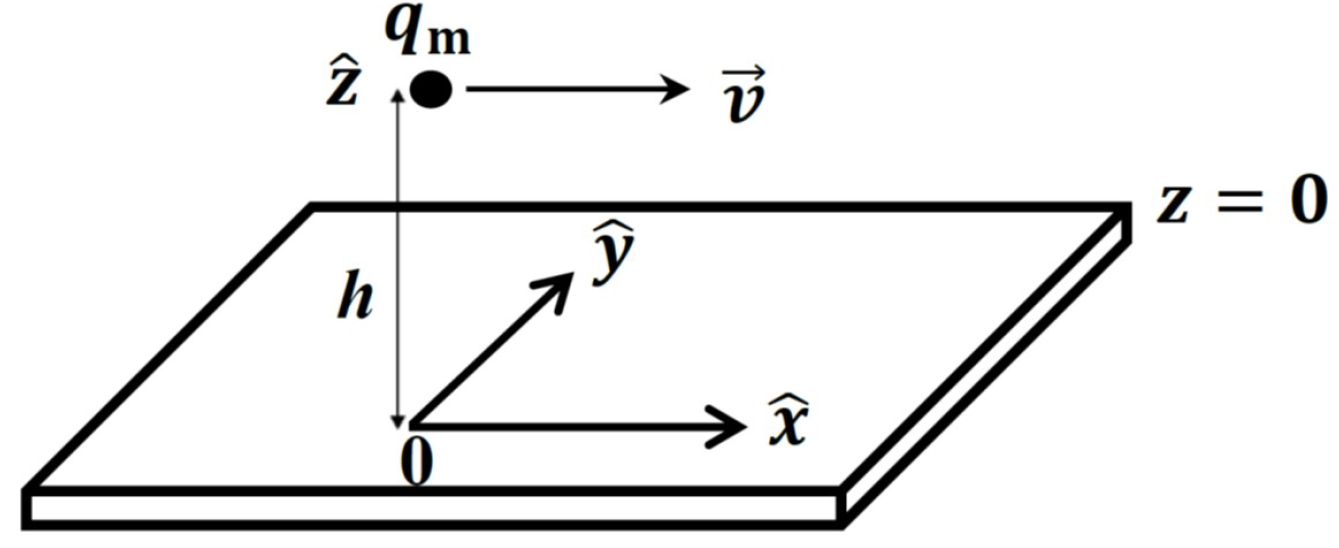
Монополь $q_{\rm m}$ (Рис. 2) движется с постоянной скоростью $v\hat{x}$, с $v\ll c,$ и на постоянной высоте, координата $z=h,$ движение происходило бесконечно долго до настоящего момента времени ($t=0$). Его координаты $(x,y)$ в данный момент времени — $(0,0)$. Будем рассматривать магнитный потенциал $\Phi_{+}$ создаваемый всеми изображениями монополя, создаваемыми этим движущимся монополем вдоль своей траектории.
Разбив траекторию монополя $q_{\rm m}$ на дискретные шаги по времени (очень маленький шаг по времени обозначим $\tau$), заменим движение $q_{\rm m}$ перепрыгиваниями в начале каждого шага. Каждое перепрыгивание — это одновременное уничтожение монополя в одной точке и создание в другой точке. Положение созданного монополя совпадает с точкой на траектории в момент начала следующего шага по времени. Положение уничтожаемого монополя совпадает с точкой траектории в начале предыдущего шага по времени. Это достигается одновременным внезапным добавлением двух монополей: $q_{\rm m}$ и $-q_{\rm m}$ в точках траектории, отвечающих начальным моментам этого и предыдущего шагов по времени. Эти две точки расположены на расстоянии $\Delta x=v\tau$. На каждом шаге магнитные монополи создают изображения. Магнитное поле будет создаваться всеми изображениями, возникшими на предыдущих шагах.
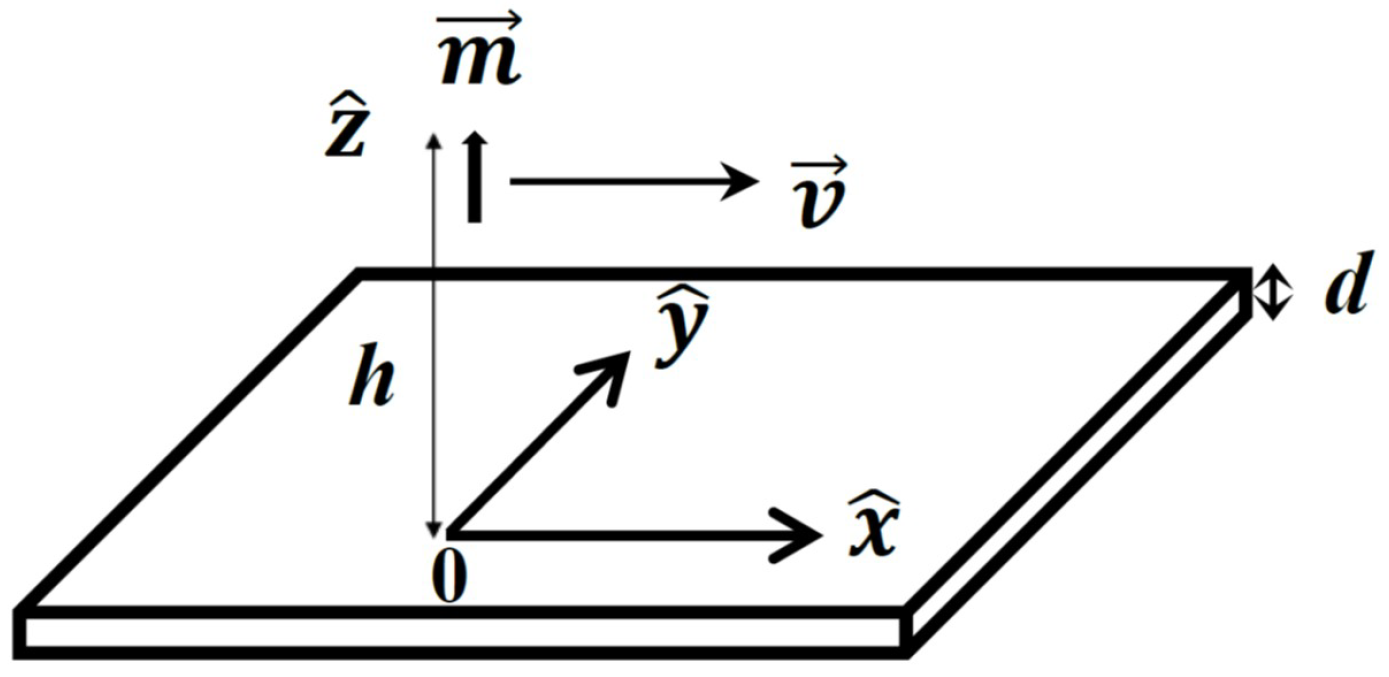
Рассмотрим движение точечного диполя, показанного на Рис. 3. Диполь с дипольным моментом $\vec{m}=m\hat{z}$, движется с постоянной скоростью $v\hat{x}$ , и на постоянной высоте ($z=h$) движение происходило до настоящего момета времени ($t=0$), в настоящий момент времени его координаты $(0,0)$. Точечный диполь можно представить как два смещенных друг относительно друга монополя, как было сказано во введении к задаче. Положением магнитного диполя считаем положение его северного монополя, считаем что магнитный момент $\vec{m}$ постоянен.
В этой Части ниже для нахождения численных значений мы рассмотрим тонкую пленку из меди, такую что $\sigma=5.9\times 10^{7}\,\, {\rm Ом}^{-1}\cdot{\rm м}^{-1}$, $d=0.50 \,\,{\rm см}$, и $h=5.0 \,\,{\rm см}$.
Известно, что глубина проникновения $\delta$ — расстояние, на которое электромагнитная волна может проникнуть вглубь проводника, зависит от циклической частоты $\omega$ волны. Эта зависимость дается формулой
$$\delta = \sqrt{\frac{2}{\omega\mu_{0}\sigma}}.$$
В дальнейшем мы будем считать, что $\omega=v_{\rm L}/h$, где скорость $v_{\rm L}$ равна большей из скоростей $v$ и $v_{0}$.
Рассмотрение выше можно применить к случаю сверхпроводника первого рода, который полностью выталкивает из себя магнитное поле (эффект Мейсснера) во все моменты времени. Для этого нужно перейти к пределу бесконечной проводимости $\sigma\rightarrow \infty$.
Здесь мы рассмотрим точечный магнитный диполь с горизонтальным дипольным моментом $\vec{m}=m\hat{x}$, массы $M_{0}$, расположенный в точке $(x,y,z)=(0,0,h)$. Рассмотрим вертикальное движение диполя под действием гравитационного поля с ускорением свободного падения $\vec{g}=-g\hat{z}$. Предположим, что при движении центра масс диполя его ориентация не меняется. Таким образом мы считаем, что магнитный момент остается постоянным в процессе движения. Также мы предполагаем, что движение происходит в вакууме и остаточное сопротивление воздуха учитывать не нужно.
Рассмотрим сферический постоянный магнит со следующими параметрами: радиус $R=1.0 \,\, {\rm мкм}$, плотность $\rho_0=7400\,\,{\rm кг}\cdot{\rm м}^{-3}$, $g=9.8\,\,{\rm м}\cdot{\rm с}^{-2}$, $\mu_{0}=4\pi\times 10^{-7}\,\,{\rm Тл}\cdot{\rm A}^{-1}\cdot{\rm м}$, намагниченность $|\vec{M}|=75\times 10^{-2}\,\,{\rm Тл}/\mu_{0}$.