
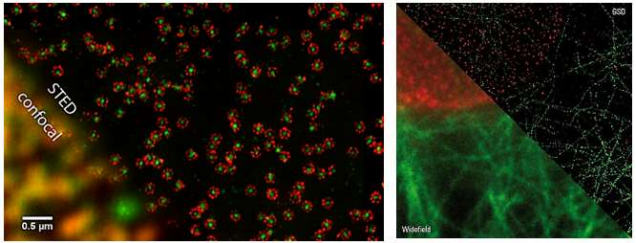
В 2004 году физики Эрик Бетциг, Уильям Мёрнер и Штефан Хель были удостоены Нобелевской премии за «создание флуоресцентной микроскопии высокого разрешения». Разработанные ими методики позволили на порядок улучшить разрешающую способность современных оптических микроскопов, хотя долгое время считалось, что оптическая микроскопия достигла своего фундаментального предела разрешения (предела Аббе).
Данная задача состоит из 3 частей. В Части A вам предлагается вывести выражение предела разрешающей способности по Аббе. В Части B вам нужно будет познакомиться с явлением флуоресценции и показать, как с ее помощью преодолеть предел Аббе. В Части C вы сможете описать метод улучшения разрешения за счет интерференции.
Объектив микроскопа формирует увеличенное действительное изображение образца. Разрешение микроскопа определяется в первую очередь свойствами объектива. При выводе выражения предела Аббе и далее рассмотрите оптическую систему, состоящую из одной тонкой линзы (объектива).
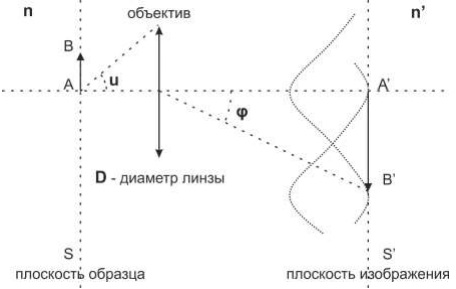
Как показано на рис. 2., тонкая линза диаметром $D$ помещена между двумя средами с разными коэффициентами преломления: $n$ – слева, со стороны образца, и $n'$ – справа, со стороны изображения. Предел разрешения – расстояние $\Delta_0=AB$ между двумя такими точечными источниками $A$ и $B$, что максимум интенсивности изображения $B$ (точка $B'$) совпадает с минимумом интенсивности изображения $A$ (точка $A'$). В вакууме направление на минимум интенсивности изображения $A'$ источника $A$ определяется из уравнений дифракции Фраунгофера на линзе $D\sin\varphi=1.22\lambda$.
При вычислениях не забудьте учесть поправки, связанные с присутствием вещества слева и справа от линзы.
Флуоресцентные молекулы и вещества способны поглощать фотоны определенной длины волны $\lambda_1$, а затем в течение короткого времени излучать фотоны с большей длиной волны $\lambda_2>\lambda_1$ (см. рис. 3). Вероятность поглощения молекулой фотона в единицу времени пропорциональна интенсивности падающего на нее излучения $I_1$ и равна $\sigma_1I_1$. Энергия в этом процессе уходит во внешнюю среду
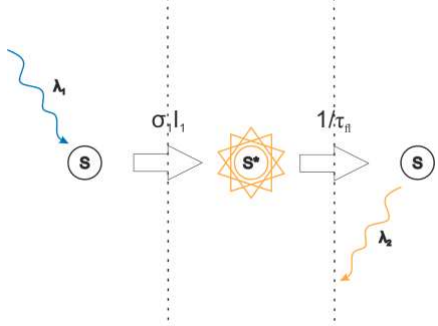
Флуоресценция подчиняется законам квантовой механики и может быть упрощенно описана следующей схемой квантовых состояний (рис. 4).
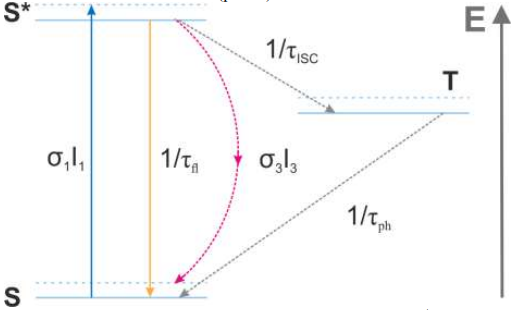
Для начала будем считать, что флуоресцентная молекула имеет $2$ состояния: основное $S$ и возбужденное $S^*$ (переходы в третье $T$ состояние очень редки). При поглощении фотона $\lambda_1$ молекула переходит из $S$ в $S^*$. С вероятностью $1/\tau_{fl}$ в единицу времени молекула в состоянии $S^*$ испускает фотон $\lambda_2$ и возвращается в $S$.
В дальнейшем используйте приближение, получившееся в пункте B2.
Рассмотрим теперь устройство флуоресцентного микроскопа (рис. 5). Излучение длиной волны $\lambda_1$ фокусируется объективом в плоскости образца. Образец, поглотив фотоны $\lambda_1$, излучает фотоны $\lambda_2$. Испущенные фотоны $\lambda_2$ проходят обратно через объектив и формируют изображение. Специальное зеркало, отражающее $\lambda_1$, но прозрачное для $\lambda_2$ используют, чтобы разделить два вида фотонов по длине волны.
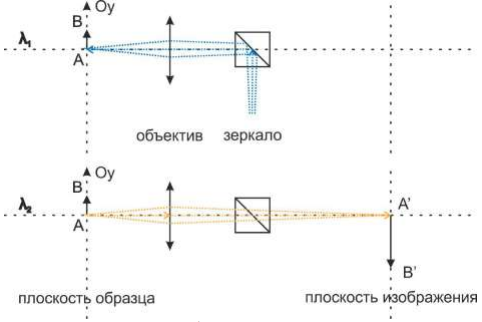
Разрешение в флуоресцентной микроскопии определяется распределением интенсивности излучения $\lambda_1$, падающего на образец. Из-за дифракции его интенсивность в плоскости образца распределена по закону
\[I_1(y)=I_1(0)\exp\left(-\cfrac{y^2}{\Delta^2_0}\right),\tag{1}\]
где $\Delta_0$ – это предел разрешения Аббе, полученный в части A.
STED (STimulated Emission Depletion)
Рассмотрим явление стимулированного излучения (STED): если на молекулу в состоянии $S^*$ падает фотон $\lambda_3>\lambda_2, \lambda_1$, молекула может вернуться в состояние $S$, испустив фотон $\lambda'_3=\lambda_3$. Вероятность такого перехода в единицу времени равна $\sigma_3I_3$ (рис. 4).
Фотоны $\lambda'_3$, испущенные при стимулированном излучении (STED) не участвуют в формировании изображения. На тех участках образца, где такие переходы происходят, уменьшается число молекул в состоянии $S^*$, а значит и число испущенных фотонов $\lambda_2$. Если максимум интенсивности излучения $\lambda_1$ на образце, совпадет с минимумом интенсивности излучения $\lambda_3$ на образце, то это сузит на нём область, где молекулы могут излучить фотоны $\lambda_2$. Размер этой области изначально был ограничен пределом разрешения $\Delta_0$ (см. формулу (1)), так что такое улучшение будет, фактически, преодолением предела Аббе.
На практике это можно сделать следующим образом. Пучок излучения $\lambda_3$ пропускают через диафрагму диаметром $d$. В центре этой диафрагмы устанавливают фазовую пластинку некоторого радиуса. Эта пластинка добавляет фазу $\pi$ прошедшим через нее лучам.
На практике часто применяются фазовые пластинки с более сложным профилем, которые дают распределение интенсивности $\lambda_3$ на образце
$$
I_3(y)=I_{3,\text{max}}\cdot{\left(\cfrac{1}{2}-\cfrac{1}{2}\cos\cfrac{\pi y}{\Delta_0}\right)}
$$
Такое распределение также имеет характерную ширину $\Delta_0$. Поскольку мы будем говорить о преодолении предела Аббе, то уместно приближение $y\ll{\Delta_0}$.
Существует два метода использования метода STED: cwSTED (continious wave STED, STED с постоянным облучением) и ptgSTED (pulsed time gated STED, STED с импульсными возбуждением и съемкой).
B5 1.00 Пусть образец облучается одновременно двумя лазерами $I_1$ (распределение интенсивности (1)), и $I_3$ (распределение интенсивности из пункта B4). Доля $N^*/N_0$ молекул, находящихся в состоянии $S^*$, может быть записана как $$\cfrac{N^*}{N_0}=A\exp\left(-\cfrac{y^2}{\Delta^2_\text{cwSTED}}\right) $$ На практике мощность $I_{3,\text{max}}$ велика, и $\sigma_3I_{3,\text{max}}\gg{\sigma_1I_1(0)}$. Найдите параметры $A$ и $\Delta_\text{cwSTED}$.
Примечание: Используйте приближение $\cfrac{1}{1+x}\approx{1-x}\approx{e^{-x}}{,}x\ll{1}$.
Обратите внимание, что величина $\Delta_\text{cwSTED}$ – предел разрешения, который определен так же, как раньше определялся предел разрешения Аббе $\Delta_0$.
B8
1.00
Пусть теперь образец облучается в течение времени $\tau_1\ll{\tau_{fl}}$ лазером $I_1$ (распределение интенсивности $(1)$), а после этого в течение времени $\tau_3$ лазером $I_3$ (распределение интенсивности из пункта B4). Доля $N^*/N_0$ молекул, находящихся в состоянии $S^*$, может быть записана как
$$\cfrac{N^*}{N_0}=A\exp\left(-\cfrac{y^2}{\Delta^2_\text{pgtSTED}}\right)
$$
На практике мощность $I_{3,\text{max}}$ велика, и $\sigma_3I_{3,\text{max}}\gg{\sigma_1I_1(0)}$. Найдите параметры $A$ и $\Delta_\text{pgtSTED}$.
Кроме состояний $S$ и $S^*$ флуоресцентная молекула имеет также третье состояние $T$. Переход $S^*\to{T}$ имеет характерное время $\tau_{ISC}$, $T\to{S}$ - $\tau_{ISC}$ и $\tau_{ph}$, причем $\tau_{ph}\gg{\tau_{ISC}\gg{\tau_{fl}}}, \frac{1}{\sigma_1I_1}$. (Считайте, что из состояния $T$ молекула не возвращается в состояние $S$ за время эксперимента.)
Пусть на образец в течение времени $\tau_1'$ падает излучение лазера $\lambda_1$ c распределением
\[I_1' = I_{1,\text{max}}'\left( \frac{1}{2} - \frac{1}{2} \cos \frac{\pi y}{\Delta_0} \right).\]
Затем в течение некоторого времени $\tau_1$ производится возбуждение флуоресценции тем же лазером $\lambda_1$, но с распределением интенсивности (1). Причем, $\tau_{fl} \ll \tau_1 \ll \tau_{ph}$. Здесь, как и ранее, справедливы приближения пунктов B2 и B4.
В части B были рассмотрены методы, позволяющие улучшить разрешение флуоресцентного микроскопа в плоскости образца. Проблема разрешения вдоль оптической оси стоит более остро – оно изначально хуже. Для решения этой проблемы применяется интерференционная микроскопия.
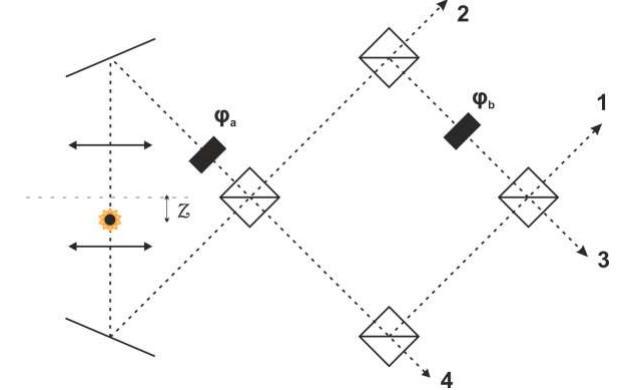
В такой установке два изображение получается двумя объективами, настроенными на одну и ту же плоскость образца. Сигналы, получаемые с помощью объективов, делятся на призмах $50:50$, причем отраженный луч набирает дополнительную фазу $\pi/2$. В оптическом пути также присутствуют две фазовые пластинки $\varphi_a=3\pi/2$, $\varphi_b=3\pi/2$. С помощью этих оптических элементов излучаемый образцом сигнал делится на несколько пучков с различными фазами и интерферирует, собираясь на детекторах $1$, $2$, $3$ и $4$. Будем считать, что в поле зрения есть единственный точечный источник, смещенный от плоскости, на которую настроены
объективы, на $z<\lambda$.