A1  ^0.50 Запишите законы движения бусинки в проекциях на радиальное и тангенциальное направления. (Считаем, что $\theta$ возрастает в направлении против часовой стрелки).

A1. 1 В радиальном направлении: $m R \dot{\theta}^{2}=N-m g \cos (\theta)-m R \sin ^{2}(\theta) \omega^{2}$	0.20
A1. 2 В касательном направлении: $m R \ddot{\theta}=m R \sin (\theta) \cos (\theta) \omega^{2}-m g \sin (\theta)-\operatorname{sgn}(\dot{\theta}) k N$ или $m R \ddot{\theta}=m R \sin (\theta) \cos (\theta) \omega^{2}-m g \sin (\theta)-fk N$, $f=1$	0.30

B1  ^1.00 Выразите углы $\theta_0$, соответствующие положению(-ям) равновесия, через $\omega$ и $\omega_c$.

B1. 1 $\theta_0 = 0$ является положением равновесия при любых $\omega$	0.40
B1. 2 Уравнение на другое положение равновесия: $\cos \theta_0 = \cfrac{g}{\omega^2 R} = \cfrac{\omega_c^2}{\omega^2}$	0.30
B1. 3 Другое положение равновесия: $\theta_0 = \pm|\arccos{\cfrac{\omega_c^2}{\omega^2}}|$	0.10
B1. 4 При $\omega<\omega_c$ существует только одно положение равновесия ($\theta_0 = 0$)	0.20

B2  ^0.50 Схематично изобразите график зависимости $\theta_0$ (по вертикальной оси) от $\omega/\omega_c$ (по горизонтальной).

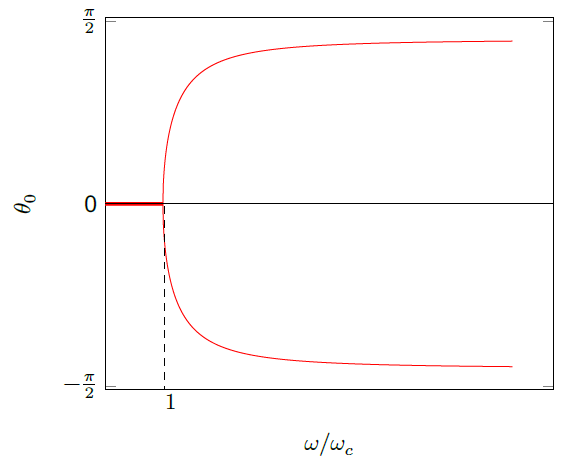
B2. 1	None
B2. 2 Верная форма графика	0.20
B2. 3 Присутствуют обе ветви	0.30

B3  ^0.50 Схематично изобразите график зависимости модуля силы нормальной реакции опоры $N$ в положении устойчивого равновесия от $\omega/\omega_c$ .

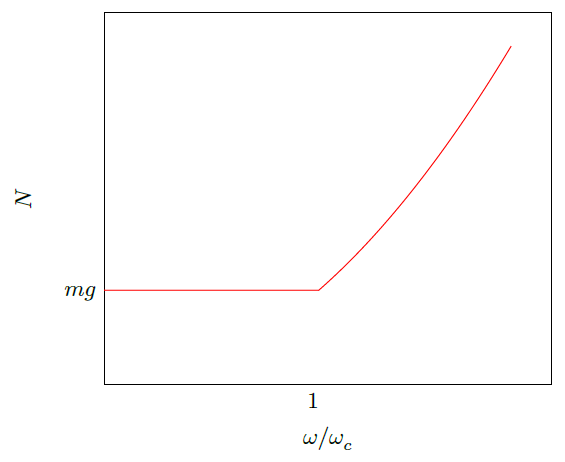
B3. 1	None
B3. 2 Верная ветвь при $\omega<\omega_c$	0.20
B3. 3 Рисунок неверный, но показано, что $N = mg$ при $\omega<\omega_c$	0.10
B3. 4 Верная ветвь при $\omega>\omega_c$	0.30
B3. 5 Рисунок неверный, но показано, что $N = m\omega^2R$ при $\omega>\omega_c$	0.10

B4  ^1.00 Пусть \(F_\theta\) — тангенциальная проекция суммы сил, действующих на бусинку. Можно определить соответствующую потенциальную энергию \(V(\theta)\) следующим образом: $$F_\theta = -\frac{1}{R}\frac{d}{d\theta}V(\theta),$$ причем примем \(V(\theta) = 0\) при \(\theta=0\).

\(V(\theta)\) представимо в виде \(V(\theta) = P+Q\cos(\theta)+S\sin^2(\theta)\). Выразите \(P,Q,S\).

B4. 1 M1 Идея интегрирования: $V-0 = \int\limits_0^V dV = -R \int\limits_0^\theta F_\theta \, d\theta$	0.30
B4. 2 M1 Проинтегрирована сила: $-R \int\limits_{0}^{\theta} F_{\theta} d \theta =\cfrac{m \omega^{2} R^{2}\left(\cos (2 \theta)-1\right)}{4}-m g R\left(\cos \theta-1\right)$	0.40
B4. 3 M1 $V(\theta)=m g R\left[(1-\cos \theta)-\cfrac{\omega^{2}}{2 \omega_{c}^{2}} \sin ^{2} \theta\right]$, т.е. $P = mgR$ $Q = -mgR$ $S = - \cfrac{\omega^2 mgR}{2 \omega_c^2}$	0.30
B4. 4 M2 Дифференцирование: $F_{\theta}=m R \sin \theta \cos \theta \, \omega^{2}-m g \sin \theta=-\cfrac{1}{R} \cfrac{d V(\theta)}{d \theta}=\cfrac{Q}{R} \sin \theta - 2 \cfrac{S}{R} \sin \theta \cos \theta$	0.30
B4. 5 M2 $Q = -mgR$	0.20
B4. 6 M2 $S = - \cfrac{\omega^2 mgR}{2 \omega_c^2}$	0.20
B4. 7 M2 $P = mgR$ (из условия $V(0) = 0$)	0.30

B5  ^1.00 \(V(\theta)\) при малых \(\theta\) представимо в виде \(V(\theta) = a(\omega)\, \theta^2 + b(\omega)\, \theta^4\). Выразите коэффициенты \(a(\omega)\) и \(b(\omega)\).

B5. 1 $a(\omega)=\cfrac{m g R}{2}\left(1-\cfrac{\omega^{2}}{\omega_{c}^{2}}\right)$	0.50
B5. 2 $b(\omega)=\cfrac{m g R}{6}\left(\cfrac{\omega^{2}}{\omega_{c}^{2}} - \cfrac{1}{4}\right)$ (отсутствие слагаемого $-\cfrac{1}{4}$ не наказывается)	0.50

B6  ^1.00 Схематично изобразите характерные графики зависимости \(V(\theta)\) от \(\theta\) для двух значений \(\omega/\omega_c\): \(\omega/\omega_c = 0.9\) и \(\omega/\omega_c = 5.0\). Количественные расчеты не требуются.

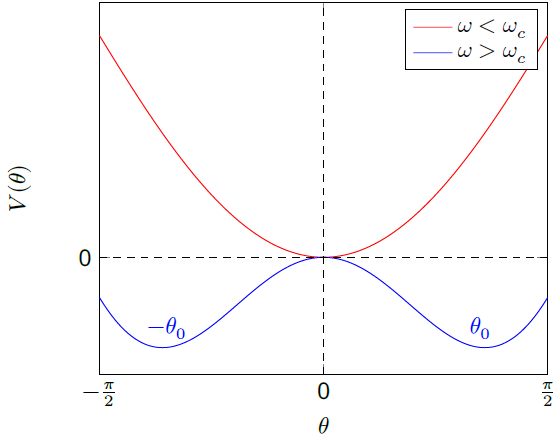
B6. 1	None
B6. 2 Кривая для $\omega<\omega_c$ (красная)	0.50
B6. 3 Кривая для $\omega>\omega_c$ (синяя)	0.50

B7  ^1.00 Теория Ландау фазовых переходов второго рода утверждает, что магнитную систему при температурах \(T\) выше критической температуры \(T_c\) можно считать парамагнитной, а при \(T < T_c\) — ферромагнитной. Зависимость намагниченности $\mathcal M$ от температуры $T$ задается формулой \(\mathcal{M}(T) = \mathcal{M}_0 \left(1 - \cfrac{T}{T_c}\right)^{1/2}\). Обозначим степень $1/2$ через $\beta$, т.е. пусть \(\mathcal{M}(T) = \mathcal{M}_0 \left(1 - \cfrac{T}{T_c}\right)^{\beta}\).

Можно сопоставить описанную теорию фазовых переходов с рассмотренной ранее механической задачей. Что в механике служит аналогом величин \(\mathcal{M}\), \(T_c\), \(T/T_c\)? Чему в механике равна \(\beta\)?

B7. 1 M1 В записи $\theta_{0}=\pm \sqrt{2}\left[1-\cfrac{\omega_{c}^{2}}{\omega^{2}}\right]^{1 / 2}$: $\mathcal M \to \theta$	0.40
B7. 2 M1 $T_c \to \cfrac{1}{\omega_c^2}$, $\cfrac{T}{T_c} \to \cfrac{\omega_c^2}{\omega^2}$	0.40
B7. 3 M1 $\beta = 1/2$	0.20
B7. 4 M2 В записи $\sin\theta_{0}=\left(1-\cfrac{\omega_{c}^{4}}{\omega^{4}}\right)^{1 / 2}$: $\mathcal M \to \sin\theta$	0.40
B7. 5 M2 $T_c \to \cfrac{1}{\omega_c^4}$, $\cfrac{T}{T_c} \to \cfrac{\omega_c^4}{\omega^4}$	0.40
B7. 6 M2 $\beta = 1/2$	0.20

B8  ^1.00 Выразите угловую частоту \(\Omega_0\) колебаний бусинки вблизи ее положения равновесия \(\theta_0\). Используйте, что для малых колебаний \(\Omega_0 = \dfrac{1}{R} \sqrt{\dfrac{V''(\theta_0)}{m}}\).

B8. 1 При $\omega < \omega_c$, т.е. когда колебания вокруг $\theta_0 = 0$: $\Omega_0 = (\omega_c^2 - \omega^2)^{1/2}$	0.50
B8. 2 При $\omega > \omega_c$: $\Omega_0 = \omega \left( 1 - \cfrac{\omega_c^4}{\omega^4} \right)^{1/2}$	0.50

B9  ^1.00 Схематично изобразите график зависимости \(\Omega_0\) от \(\omega\).

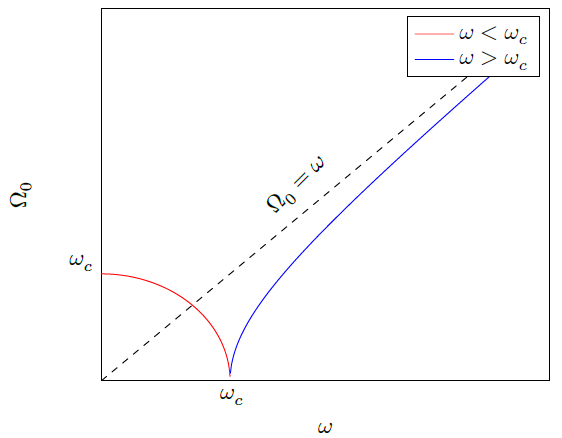
B9. 1	None
B9. 2 Верная ветвь при $\omega<\omega_c$ (или верно построена по неверно полученному выражению)	0.50
B9. 3 Верная ветвь при $\omega>\omega_c$ (или верно построена по неверно полученному выражению)	0.50

C1  ^1.00 Примите $f=1$, а вместо $k$ введите выражение $k = \operatorname{tg} \alpha$. Условие на положение(-я) равновесия $\theta_0$ можно переписать в виде: $ \left(\dfrac{\omega}{\omega_c}\right)^2 = \dfrac{\operatorname{tg} x}{\sin y}$.
Найдите $x$ и $y$.

C1. 1 $\ddot{\theta}=\omega_{c}^{2}\left[\sin \theta\,(\cos \theta-f k \sin\theta)\left(\cfrac{\omega}{\omega_{c}}\right)^{2}-\sin \theta-f k \cos \theta-f k\left(\cfrac{\dot{\theta}}{\omega_{c}}\right)^{2}\right]$	0.20
C1. 2 $\sin \theta_{0}\left(\cos \theta_{0}-f k \sin \theta_{0}\right)\left(\cfrac{\omega}{\omega_{c}}\right)^{2}=\sin \theta_{0}+f k \cos \theta_{0}$	0.40
C1. 3 $x = \theta_0 + \alpha$ $y = \theta_0$	0.40
C1. 4 Из-за алгебраической ошибки получено $x = \theta_0 - \alpha$	-0.10

C2  ^0.50 Пусть $f =1$ и $k = 0.05$. Вычислите углы $\theta_0$ в положениях равновесия для двух случаев:
— \(\omega/\omega_c\) = 0.50
— \(\omega/\omega_c\) = 0.70

C2. 1 Замечено, что $k = 0.05 \ll 1$, поэтому: $\sin \theta_0 \approx \theta_0$, $\mathrm{tg} (\theta_0 + \alpha) \approx \theta_0 + \alpha$	0.20
C2. 2 $\left(\cfrac{\omega}{\omega_{c}}\right)^{2} \approx 1+\cfrac{k}{\theta_{0}}$, поэтому: — $\theta_0 = -0.07~\text{рад.}$ при $\cfrac{\omega}{\omega_c} = 0.50$ — $\theta_0 = -0.1~\text{рад.}$ при $\cfrac{\omega}{\omega_c} = 0.70$	0.30