В фазовом переходе второго рода «парамагнетик-ферромагнетик» свободная энергия (механический аналог которой — потенциальная энергия) зависит от намагниченности по следующему закону:
$$V(\mathcal{M})=a(T)\mathcal{M}^2+b(T)\mathcal{M}^4,$$
где \(T\) — температура, \(b(T) > 0\), \(a(T)\) может менять знак в зависимости от \(T\).

Теоретическое описание этого фазового перехода, как будет показано в процессе решения задачи, перекликается с рассмотрением следующей механической системы.

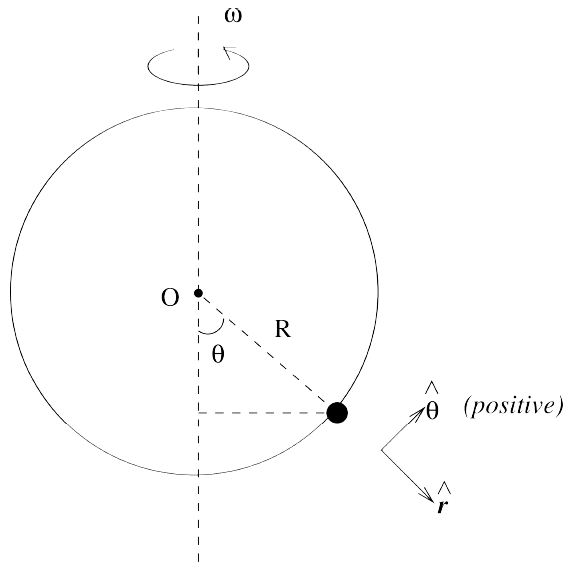
На кольцо радиуса \(R\) надета маленькая бусинка массы \(m\). Кольцо может вращаться вокруг своего вертикального диаметра с угловой скоростью \(\omega\) (рис. 1). Сила \(F_f\) направлена против скольжения бусинки по кольцу, пропорциональна силе нормальной реакции опоры \(N\) и равна \(F_f = fkN\), где число \(f\) может принимать значения \(1\) и \(-1\): пусть \(f=+1\), когда бусинка движется против часовой стрелки (в сторону возрастания угла \(\theta\)), и \(f=-1\), если наоборот. Таким образом, \(f=\operatorname{sign}\dot\theta\) (равно \(+1\) или \(-1\) в зависимости от знака \(\dot{\theta}\)).

Используйте полярные координаты \({r, \theta}\). Ответы выражайте через \(\omega_c=\sqrt{g/R}\) (\(g\) — ускорение свободного падения).

$\textit{Примечания.}$
При вращении материальной точки по окружности радиуса \(R\) можно рассчитать скорость как \(\dot{\vec{r}} = R \dot{\theta} \hat{{\theta}}\) и ускорение как \(\ddot{\vec{r}} = -R \dot{\theta}^2 \hat{{r}} + R \ddot{\theta} \hat{{\theta}}\), где введены единичные вектора \(\hat{r}\) (вдоль радиуса) и \(\hat{{\theta}}\) (вдоль касательной).
Также можете пользоваться разложениями (здесь \(\theta\) - в радианах, \(|x| \ll 1\)):

\(\sin⁡\theta=\theta−\cfrac{\theta^3}{6}+\dots\)

\(\cos⁡\theta=1−\cfrac{\theta^2}{2}+\cfrac{\theta^4}{24}+\dots\)

\((1+x)^n=1+nx+\cfrac{n(n−1)}{2}x^2+\cfrac{n(n−1)(n−2)}{6}x^3+\dots\)

Перейдем в систему отсчета вращающегося кольца. Будем рассматривать углы \(−\pi/2<\theta<\pi/2\). На рисунке 2 показаны силы, действующие на бусинку. Силами, не указанными на рисунке, можно пренебречь.

A1  ^0.50 Запишите законы движения бусинки в проекциях на радиальное и тангенциальное направления. (Считаем, что $\theta$ возрастает в направлении против часовой стрелки).

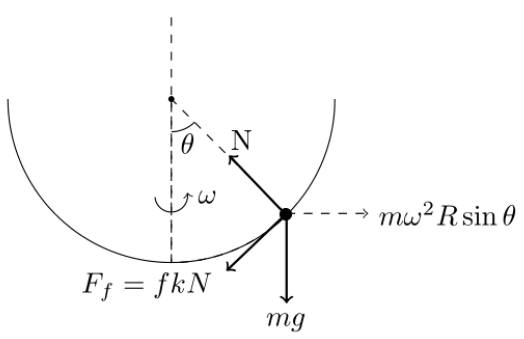
В пунктах с B.1 по B.9 считайте, что $k=0$.

B1  ^1.00 Выразите углы $\theta_0$, соответствующие положению(-ям) равновесия, через $\omega$ и $\omega_c$.

B2  ^0.50 Схематично изобразите график зависимости $\theta_0$ (по вертикальной оси) от $\omega/\omega_c$ (по горизонтальной).

B3  ^0.50 Схематично изобразите график зависимости модуля силы нормальной реакции опоры $N$ в положении устойчивого равновесия от $\omega/\omega_c$ .

B4  ^1.00 Пусть \(F_\theta\) — тангенциальная проекция суммы сил, действующих на бусинку. Можно определить соответствующую потенциальную энергию \(V(\theta)\) следующим образом: $$F_\theta = -\frac{1}{R}\frac{d}{d\theta}V(\theta),$$ причем примем \(V(\theta) = 0\) при \(\theta=0\).

\(V(\theta)\) представимо в виде \(V(\theta) = P+Q\cos(\theta)+S\sin^2(\theta)\). Выразите \(P,Q,S\).

B5  ^1.00 \(V(\theta)\) при малых \(\theta\) представимо в виде \(V(\theta) = a(\omega)\, \theta^2 + b(\omega)\, \theta^4\). Выразите коэффициенты \(a(\omega)\) и \(b(\omega)\).

B6  ^1.00 Схематично изобразите характерные графики зависимости \(V(\theta)\) от \(\theta\) для двух значений \(\omega/\omega_c\): \(\omega/\omega_c = 0.9\) и \(\omega/\omega_c = 5.0\). Количественные расчеты не требуются.

B7  ^1.00 Теория Ландау фазовых переходов второго рода утверждает, что магнитную систему при температурах \(T\) выше критической температуры \(T_c\) можно считать парамагнитной, а при \(T < T_c\) — ферромагнитной. Зависимость намагниченности $\mathcal M$ от температуры $T$ задается формулой \(\mathcal{M}(T) = \mathcal{M}_0 \left(1 - \cfrac{T}{T_c}\right)^{1/2}\). Обозначим степень $1/2$ через $\beta$, т.е. пусть \(\mathcal{M}(T) = \mathcal{M}_0 \left(1 - \cfrac{T}{T_c}\right)^{\beta}\).

Можно сопоставить описанную теорию фазовых переходов с рассмотренной ранее механической задачей. Что в механике служит аналогом величин \(\mathcal{M}\), \(T_c\), \(T/T_c\)? Чему в механике равна \(\beta\)?

B8  ^1.00 Выразите угловую частоту \(\Omega_0\) колебаний бусинки вблизи ее положения равновесия \(\theta_0\). Используйте, что для малых колебаний \(\Omega_0 = \dfrac{1}{R} \sqrt{\dfrac{V''(\theta_0)}{m}}\).

B9  ^1.00 Схематично изобразите график зависимости \(\Omega_0\) от \(\omega\).

В оставшихся пунктах C.1 и C.2 считайте, что $k \ne 0$.

C1  ^1.00 Примите $f=1$, а вместо $k$ введите выражение $k = \operatorname{tg} \alpha$. Условие на положение(-я) равновесия $\theta_0$ можно переписать в виде: $ \left(\dfrac{\omega}{\omega_c}\right)^2 = \dfrac{\operatorname{tg} x}{\sin y}$.
Найдите $x$ и $y$.

C2  ^0.50 Пусть $f =1$ и $k = 0.05$. Вычислите углы $\theta_0$ в положениях равновесия для двух случаев:
— \(\omega/\omega_c\) = 0.50
— \(\omega/\omega_c\) = 0.70