
Период колебаний математического маятника определяется по формуле
\begin{equation}
T=2\pi \sqrt{\frac{l}{g}},
\end{equation}
где $g$ — ускорение свободного падения в данный момент времени суток.
Различие в периодах колебаний маятника в полдень и полночь обусловлено влиянием Солнца: гравитационным притяжением и центробежной силой, обусловленной движением Земли вокруг Солнца. Используя формулу для периода колебаний маятника, относительное изменение периода можно представить в виде:
\begin{equation}
\varepsilon =\frac{T_2-T_1}{T_1}=\sqrt{\frac{g_1}{g_2}}-1,
\end{equation}
где $g_1,g_2$ — ускорения свободного падения в полдень и полночь, соответственно.
Направления вращения Земли вокруг собственной оси и вокруг Солнца совпадают, как показано на рисунке 1. Направления действия гравитационных и центробежных сил в полдень и полночь оказываются различными, как показано на рисунке 2.
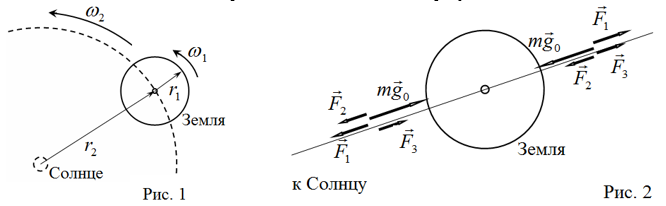
На рисунке 2: $mg_0$ — сила гравитационного притяжения к Земле; $F_1$ — центробежная сила, обусловленная вращением Земли вокруг собственной оси; $F_2$ — сила гравитационного притяжения к Солнцу; $F_3$ — центробежная сила, обусловленная движением Земли вокруг Солнца.
Тогда ускорения свободного падения с учетом влияния Солнца будет определяться выражениями:
В полдень:
\begin{equation}
g_1=g_0-{\omega }^2_1r_1-G\frac{M}{{\left(r_2-r_1\right)}^2}+{\omega }^2_2r_2.
\end{equation}
В полночь:
\begin{equation}
g_2=g_0-{\omega }^2_1r_1+G\frac{M}{{\left(r_2+r_1\right)}^2}-{\omega }^2_2r_2.
\end{equation}
В этих формулах $M$ — масса Солнца, $G$ — гравитационная постоянная.
Для упрощения полученных выражений используем уравнение, описывающее движение Земли вокруг Солнца:
\begin{equation}
G\frac{M}{r^2_2}={\omega }^2_2r_2.
\end{equation}
С учетом этого соотношения, разность ускорений представляется в виде
\begin{equation}
\Delta g=g_1-g_2={\omega }^2_2r_2\left(2-{\left(1-\frac{r_1}{r_2}\right)}^{-2}-{\left(1+\frac{r_1}{r_2}\right)}^{-2}\right).
\end{equation}
Заметим, что в данном случае для того, чтобы получить не нулевой результат в разложении степенных функций, необходимо учитывать и квадратичное слагаемое (т.е. $\left(1+x\right)^{-2} \approx 1-2x+3x^{2} $):
\begin{equation}
\Delta g={-6\omega }^2_2r_2{\left(\frac{r_1}{r_2}\right)}^2.
\end{equation}
Таким образом, относительное изменение периода колебаний, обусловленное влиянием Солнца, оказывается равным
\begin{equation}
\varepsilon \approx \frac{\Delta g}{2g_2}\approx \frac{\Delta g}{2g_0},
\end{equation}
откуда получаем окончательный ответ