
Выразим скорость электрона через его импульс:
$$
v_x = \frac{\partial \varepsilon}{\partial p_x} = \varepsilon_0 a \sin (a p_x),
$$
аналогично для остальных двух компонент
$$
v_y = \varepsilon_0 a \sin(a p_y), \; v_z = \varepsilon_0 a \sin(a p_z).
$$
Из уравнения движения $\dfrac{d}{dt}\vec{p} = \vec{F}$. Выразим ускорение через производную импульса:
$$
a_x = \dot{v}_x = \varepsilon_0 a^2 \cos (a p _x) \dot{p}_x = \varepsilon_0 a^2 \cos(a p_x) F_x.
$$
Формулы остальных компонент аналогичны. Для значений импульса из условия
На электрон действует сила $F_x = - q E$, поэтому импульс
$$
p_x = - q E t,
$$
а соответствующая скорость
$$
v_x = -a \varepsilon_0 \sin(aqE t).
$$
Остальные проекции скорости равны нулю. Интегрируя, найдем зависимость координаты $x$ от времени
Плотность тока выражается через скорость и концентрацию электронов
$$
j_x = - n q v_x = n q a \varepsilon_0 \sin (a q E t).
$$
Уравнение движения
$$
\dot{\vec{p}} = - q \vec{v} \times \vec{B}.
$$
Производная энергии по времени
$$
\frac{d \varepsilon} {dt} = \frac{\partial \varepsilon}{\partial p_x} \dot{p}_x + \frac{\partial \varepsilon}{\partial p_y} \dot{p}_y +\frac{\partial \varepsilon}{\partial p_z} \dot{p}_z = v_x \dot{p}_x + v_y \dot{p}_y + v_z \dot {p}_z = \vec{v} \dot{\vec{p}}.
$$
Подставляя выражение для производной импульса, получим
$$
\dot{\varepsilon} = \vec{v} \cdot\left(- q \vec{v} \times \vec{B}\right) = 0.
$$
Умножив уравнение движения скалярно на магнитное поле получим
$$
\frac{d}{dt} (\vec{B}{\vec{p}}) = \vec{B} \dot{\vec{p}} = - q \vec{B} (\vec{v} \times \vec{B}) = 0,
$$
то есть проекция импульса на магнитное поле постоянна.
Запишем уравнения движения:
\begin{align*}
m_x\dot{v}_x &= - q v_y B;\\
m_y \dot{v}_y &= q v_x B.
\end{align*}
Исключим из первого уравнения $v_y$ продифференцировав его и выразив $\dot{v}_y$ из второго уравнения. Получим
$$
m_x \ddot{v}_x = - q \dot{v}_y B = - \frac{q^2 B^2}{m_y} v_x,
$$
то есть
$$
\ddot{v}_x = - \frac{q^2 B^2}{m_x m_y} v_x.
$$
Это уравнение гармонических колебаний с частотой
$$
\omega = \frac{qB}{\sqrt{m_x m_y}}.
$$
Зависимость скорости от времени имеет вид
$$
v_x = A \cos (\omega t + \varphi),
$$
где амплитуду $A$ можно найти, зная энергию электрона:
$$
A = \sqrt{\frac{2\varepsilon}{m_x}}.
$$
Вторую компоненту скорости можно найти из уравнения движения
$$
v_y = - \frac{m_x}{q B} \dot{v}_x = \sqrt{\frac{2\varepsilon}{m_x}} \frac{\omega}{qB} \sin(\omega t + \varphi) = \sqrt{\frac{2 \varepsilon}{m_y}} \sin (\omega t + \varphi).
$$
Интегрируя, получим траекторию частицы
\begin{align*}
x(t) &= \sqrt{\frac{2 \varepsilon}{m_x}} \frac{1}{\omega} \sin(\omega t + \varphi) = \frac{\sqrt{2 m_y \varepsilon}}{q B} \sin (\omega t + \varphi);\\
y(t ) &= - \frac{\sqrt{2 m_x \varepsilon}}{qB} \cos (\omega t + \varphi).
\end{align*}
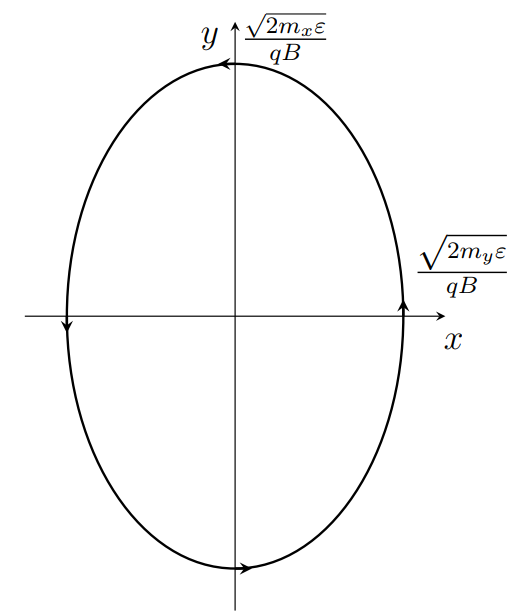
Таким образом, траектория представляет собой эллипс с полуосями
$$
A_x = \frac{\sqrt{2 m_y \varepsilon}}{q B},\; A_y = \frac{\sqrt{2 m_x \varepsilon}}{qB}.
$$
Движение происходит против часовой стрелки.
С учетом электрического поля уравнения движения
\begin{align*}
m_x\dot{v}_x &= -qE- q v_y B;\\
m_y \dot{v}_y &= q v_x B.
\end{align*}
Введем новую переменную $u_y$ с помощью соотношения
$$
v_y = - \frac{E}{B} + u_y,
$$
тогда уравнения движения примут такой же вид, как и в предыдущей части:
\begin{align*}
m_x\dot{v}_x &= - q u_y B;\\
m_y \dot{u}_y &= q v_x B.
\end{align*}
Начальные условия
$$
v_x (0) = 0 ,\; v_y(0) = 0, \; u_y(0) = \frac{E}{B}.
$$
С учетом этого решение
$$
v_x = -\sqrt{\frac{m_y}{m_x}}\frac{E}{B} \sin \omega t;\; v_y =- \frac{E}{B}(1- \cos \omega t).
$$
Тогда импульсы
$$
p_x =- \sqrt{m_x m_y} \frac{E}{B} \sin \omega t, \;
p_y = -m_y \frac{E}{B}(1 - \cos \omega t ).
$$
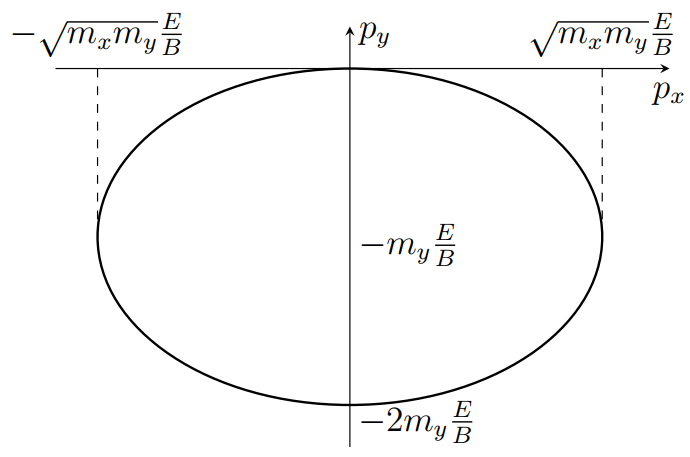
Интегрируя скорости из предыдущего пункта, получим
Запишем уравнения движения
$$
\dot{\vec{p}} = - q \vec{v} \times \vec{B} = - q \dot{\vec{r}}\times \vec{B}.
$$
Интегрируя, получаем
$$
\Delta \vec{p} = - q \Delta \vec{r} \times \vec{B}.
$$
Умножим это равенство векторно на $\vec{B}$.
$$
\Delta \vec{p} \times \vec{B} = - q(\Delta \vec{r} \times \vec{B}) \times \vec{B} = q B^2 \Delta \vec{r}.
$$
Таким образом, вектор перемещения можно выразить через изменение импульса
$$
\Delta \vec{r} = \frac{1}{qB^2} \Delta \vec{p} \times \vec{B}.
$$
Рассмотрим сначала в импульсном пространстве. Из постоянства энергии следует, что годограф импульса — поверхность
$$
\frac{p^2_y}{2m_y} + \varepsilon_0 (1 - \cos ap_x) = \varepsilon = const.
$$
Уравнение этой поверхности можно представить в виде
$$
p_y = \pm \sqrt{2 m_y (\varepsilon - \varepsilon _0 + \varepsilon _0 \cos a p_x)}.
$$
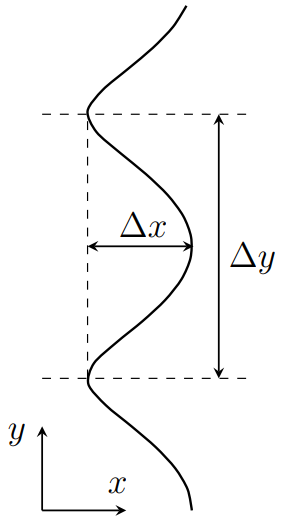
В том случае, если $\varepsilon \le 2 \varepsilon_0$, годограф представляет собой замкнутую кривую. Тогда траектория также будет замкнутой кривой. Если же $\varepsilon > 2 \varepsilon_0$, годограф импульса — незамкнутая кривая, направленная вдоль оси $x$. Тогда траектория движения частицы - кривая, направленная вдоль $y$, причем зависимость $x(y)$ — периодическая. Найдем период этой функции и ширину полосы вдоль оси $x$, которую она занимает.
$$
\Delta y = \frac{1}{qB} \frac{2\pi}{a}, \; \Delta x = \frac{1}{qB} \Delta p_y = \frac{\sqrt{2 m_y}}{qB} (\sqrt{\varepsilon} - \sqrt{\varepsilon - 2 \varepsilon _0}).
$$
Запишем законы сохранения энергии и импульса:
$$
u p = u q_1 + u q_2,\; \vec{p} = \vec{q}_1 + \vec{q}_2.
$$
Поскольку длина вектора $\vec{p}$ равна сумме длин остальных двух векторов, все три вектора должны быть направлены в одну и ту же сторону.
Из закона сохранения импульса
$$
\vec{q}_2 = \vec{p} - \vec{q}_1.
$$
Отсюда
$$
q_2^2 = p^2 + q_1^2 - 2 p q_1 \cos \theta_1 = p^2 + q_1^2 - 2 p q_1 (1 - \theta_1^2/2) = (p - q_1)^2+ p q_1 \theta_1^2.
$$
Извлечем корень и разложим в ряд до требуемого порядка
$$
q_2 = \sqrt{ (p - q_1)^2+ p q_1 \theta_1^2} \approx p - q_1 + \frac{p q_1}{2(p - q_1)} \theta_1^2
$$
Запишем закон сохранения энергии
$$
u p + \alpha p^3 = u q_1 + \alpha q_1^3 + u q_2 + \alpha q_2^3.
$$
Подставим выражение для $q_2$:
$$
u p + \alpha p^3 = u q_1 + \alpha q_1^3 + u \left(p - q_1 + \frac{p q_1}{2(p - q_1)} \theta_1^2\right) + \alpha \left( p - q_1 + \frac{p q_1}{2(p - q_1)} \theta_1^2\right)^3.
$$
Раскроем скобки и оставим вклады порядка $\theta_1^2$:
$$
\alpha p^3 = \alpha q^3 + \frac{u p q_1}{2 (p - q_1)} \theta_1^2 +\alpha (p - q_1)^3 + \frac{3 \alpha}{2} p q_1 (p - q_1)\theta_1^2.
$$
Перенесем слагаемые, не зависящие от угла, налево:
$$
\alpha (p^3 - q_1^3 - (p-q_1)^3) = \frac{u p q_1 \theta_1^2}{2(p - q_1)}
\left( 1 + \frac{3 \alpha}{u } (p - q_1)^2\right).$$
Вторым слагаемым в скобках в правой части можно пренебречь в силу условия $\alpha p^3 \ll u p$, в левой части раскроем скобки и получим
$$
3 \alpha (p - q_1) p q_1 = \frac{u p q_1 \theta_1^2}{2(p - q_1)}.
$$
Отсюда
$$
(p-q_1 )^2 = \frac{u }{6 \alpha} \theta_1^2, \; q_1 = p - \sqrt{\frac{u}{6 \alpha}} \theta_1.
$$
У уравнения в предыдущем пункте есть решение, если $\alpha > 0$.
Максимальный угол достигается при минимальном импульсе испускаемого фонона $q_1 \to 0$. Тогда из выражения для $q_1$ находим
$$
\theta_{\max} = \sqrt{\frac{6 \alpha}{u}} p.
$$
Вся задача решалась в приближении малых углов. Это приближение работает при условии $\theta_{max} \ll 1$, то есть
$$
p \ll \sqrt{\frac{u}{\alpha}}.
$$
Из результатов $\mathrm{C3}$ следует, что импульсы фононов выражаются через углы излучения как
$$
q_1 = p - \sqrt{\frac{u}{6 \alpha}} \theta_1, \; q_2 = p - \sqrt{\frac{u}{6 \alpha}} \theta_2.
$$
Запишем проекцию закона сохранения импульса на ось, перпендикулярную направлению движения исходного фонона:
\begin{align*}
q_1 \theta_1 &= q_2 \theta_2, \\
p \theta_1 - \sqrt{\frac{u}{6 \alpha}} \theta_1^2 &= p \theta_2 - \sqrt{\frac{u}{6 \alpha}} \theta_2^2.
\end{align*}
Перегруппируем слагаемые:
$$
p(\theta_1 - \theta_2) = \sqrt{\frac{u}{6 \alpha}} (\theta_1^2 -\theta_2^2), \;
p = \sqrt{\frac{u}{6 \alpha}} (\theta_1 + \theta_2).
$$