Введение

При исследовании характера движения механических систем часто удобно использовать воображаемое пространство, по осям которого откладываются координаты и импульсы всех материальных точек системы (или их скорости, т.е. производные от координат по времени), — фазовое пространство. Каждая точка этого воображаемого пространства, называемая изображающей точкой, полностью задает некоторое состояние системы.

При движении механической системы ее изображающая точка описывает в фазовом пространстве некоторую кривую, называемую фазовой траекторией. Направление движения изображающей точки указывается стрелкой на фазовой траектории. Набор всех возможных фазовых траекторий данной системы называют ее фазовым портретом. Анализ этого фазового портрета позволяет выяснить важные качественные особенности движения системы без решения уравнений движения системы в явном виде. В ряде случаев использование фазового пространства является самым адекватным методом рассмотрения и решения проблемы.

В данной задаче мы предлагаем использовать фазовое пространство для анализа различных механических систем с одной степенью свободы, т.е. описываемых только одной координатой. В этом случае фазовое пространство является плоскостью. Фазовые траектории в этом случае задаются зависимостью импульса точки от ее координаты (или наоборот).

Например, фазовый портрет свободной частицы движущейся вдоль оси $x$ будет выглядеть следующим образом (рис. 1):

Часть A. Фазовые портреты (3 балла)

A1  ^0.50 Нарисуйте качественно фазовую траекторию свободной частицы, движущейся между двумя параллельными упруго отражающими стенками, расположенными в точках с координатами $x = - L/2$ и $x =
L/2$.

A2  ^1.00 Исследуйте фазовые траектории гармонического осциллятора, т.е. частицы с массой $m$, на которую действует упругая сила $F = -k x$.

Найдите уравнение фазовой траектории и параметры этой траектории. Нарисуйте качественно пример фазовой траектории гармонического осциллятора.

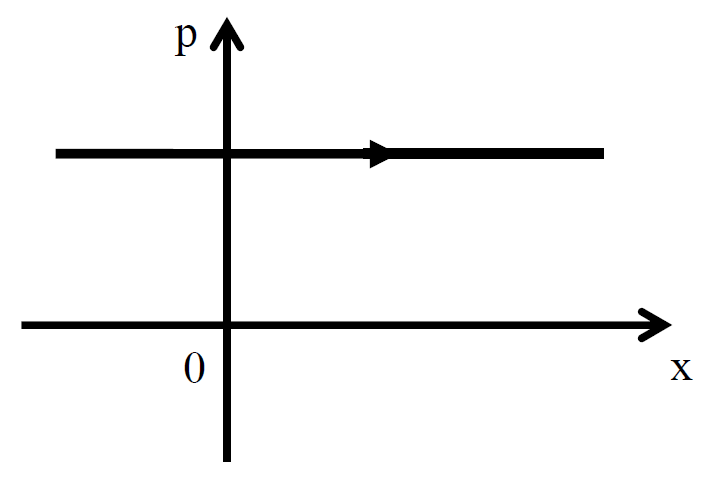
Рассмотрим точечную частицу массы $m$, подвешенную на невесомом, абсолютно твердом стержне длины $L$ в поле тяжести земли. В качестве координаты в этом случае удобно выбирать угол отклонения стержня от вертикали $\alpha$. В качестве фазовой плоскости можно выбрать плоскость с координатами ($\alpha$, $d\alpha/dt$).

A3  ^1.50 Исследуйте качественно фазовый портрет этого математического маятника при произвольных углах отклонения $\alpha$ и нарисуйте его. Сколько качественно различных типов $K$ фазовых траекторий существует у этой системы? Найдите условия, которыми определяются эти различные типы фазовых траекторий. Можете не рассматривать в качестве фазовых траекторий сами точки равновесия.

Часть B. Осциллятор с трением скольжения (7 баллов)

При учете сил сопротивления мы сталкиваемся с двумя различными видами сил трения. В первом случае сила трения зависят от величины скорости — вязкое трение — и описываются выражением $\vec{F}_{тр} = -\gamma \vec{v}$. Во втором случае сила трения не зависит от величины скорости, определяется коэффициентом трения $F_{тр} = \mu N$ и направлена против относительной скорости соприкасающихся тел — сила трения скольжения. Первый случай реализуется при движении тела в газах или жидкостях. Второй — при скольжении одного тела по поверхности другого.

В качестве примера второго случая рассмотрите тело на пружине на горизонтальной плоскости с трением. Масса тела равна $m$, коэффициент упругости пружины равен $k$, коэффициент трения скольжения тела о плоскость равен $\mu$. Тело движется по прямой линии, которую можно считать осью $x$ (положение тела при $x = 0$ соответствует нерастянутой пружине). В начальный момент тело расположено в точке $x=A_0$ с нулевой скоростью.

B1  ^1.00 Запишите уравнение движения гармонического осциллятора, на который действует сила трения скольжения.

B2  ^2.00 Нарисуйте качественно фазовую траекторию.

B3  ^1.00 Останавливается ли тело в положении, когда пружина не растянута? Если нет, то какова ширина области, в которой может остановиться тело?

B4  ^1.50 Найдите величину изменения максимального отклонения осциллятора в положительном направлении $x$ в течение одного полного колебания $\Delta A$. Найдите время между двумя последовательными максимальными отклонениями в положительном направлении. Найдите также зависимость этого максимального отклонения от времени $A(t_n)$, где $t_n$ — время достижения $n$-ого максимума.

B5  ^1.00 Нарисуйте качественно график зависимости координаты от времени $x(t)$ и оцените число $N$ совершаемых телом колебаний.

Указание: Уравнение эллипса с центром в начале координат с полуосями $a$ и $b$ имеет вид:
\begin{equation*}
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.
\end{equation*}