Введение. Метод изображений

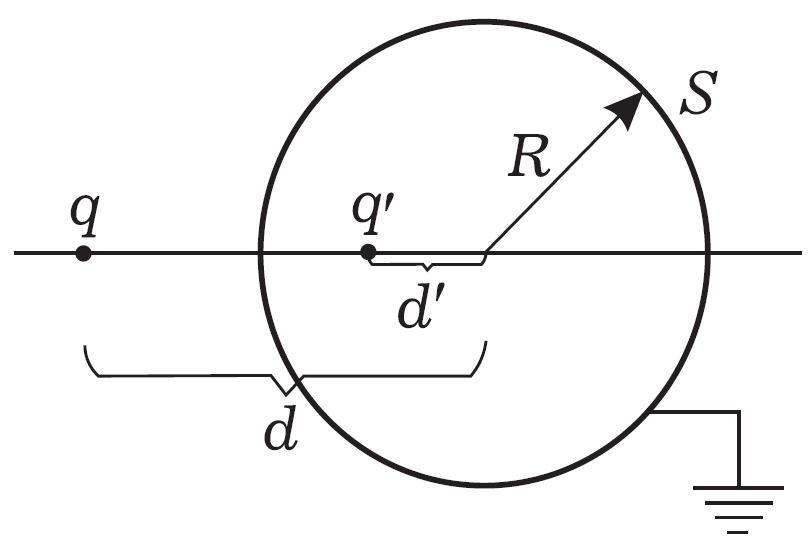
На расстоянии $d$ от центра металлической заземленной сферы $S$ радиуса $R$ находится точечный заряд $q$. При этом на сфере появляется индуцированный заряд, распределенный по ее поверхности с некоторой поверхностной плотностью. Электрическое поле и потенциал, которые создают заряды, индуцированные на поверхности сферы, совпадают с электрическим полем и потенциалом, создаваемыми одним точечным зарядом $q'$, который находится внутри сферы (рис. 1).

Часть A. Заряд-изображение

A1  ^0.30 Чему равен потенциал сферы?

A2  ^1.90 Выразите $q'$ и $d'$ (расстояние от центра сферы $S$ до заряда-изображения $q'$) через величины $q$, $d$ и $R$.

A3  ^0.50 Получите выражение для силы, которая действует на заряд $q$. Отталкивающая ли эта сила?

Часть B. Электрическое поле, экранированное сферой

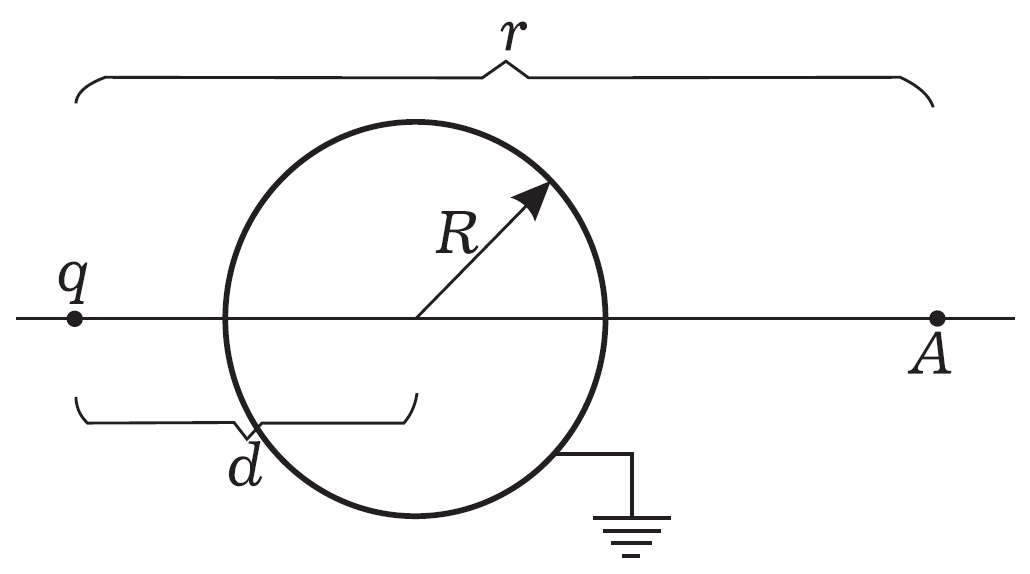
Точечный заряд находится на расстоянии $d$ от центра заземленной металлической сферы радиуса $R$. Необходимо определить, как влияет заземленная металлическая сфера на электрическое поле в точке $A$ с противоположной стороны сферы (рис. 2). Точка $A$ находится на прямой, соединяющей заряд $q$ и центр сферы. Расстояние от точки $A$ до точечного заряда $q$ равно $r$.

B1  ^0.60 Определите вектор напряженности электрического поля в точке $A$.

B2  ^0.60 Запишите выражение для напряженности электрического поля на большом расстоянии $r$ от заряда ($r \gg d$). Используйте приближение $(1+a)^{-2} \approx 1 - 2a$, при $a \ll 1$.

B3  ^0.30 Определите расстояние $d$, при котором заземленная металлическая сфера полностью экранирует поле заряда $q$ (напряженность поля в точке $A$ равна 0).

Часть C. Малые колебания в поле заземленной металлической сферы

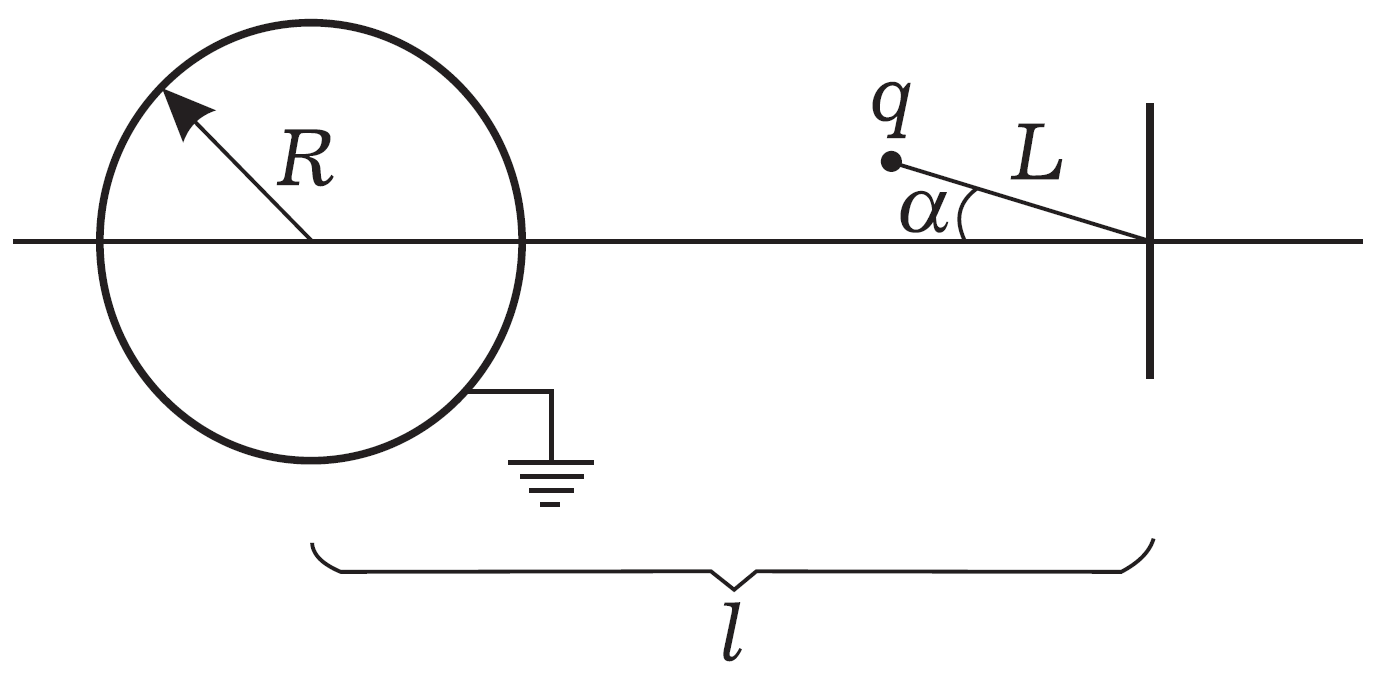
Точечный заряд $q$ массой $m$ подвешен на нити длиной $L$, закрепленной на стене вблизи заземленной металлической сферы. Точка, в которой нить крепится к стене, находится на расстоянии $l$ от центра сферы. При решении этой части не учитывайте электростатическое влияние стены, а также действие гравитационных сил. Точечный заряд рассматривайте как математический маятник (рис. 3).

C1  ^0.80 Определите силу, которая действует на заряд $q$ при заданном угле $\alpha$. Укажите направление силы на рисунке.

C2  ^0.80 Выразите проекцию этой силы на ось, перпендикулярную нити, через $l$, $L$, $R$, $q$ и $\alpha$.

C3  ^1.00 Определите частоту малых колебаний маятника.

Часть D. Электростатическая энергия системы

Вычислим энергию электростатического взаимодействия в такой системе. Не забудьте про взаимодействие между самими индуцированными зарядами. Считайте известными заряд $q$, радиус сферы $R$ и расстояние $d$.

D1  ^1.00 Найдите электростатическую энергию взаимодействия заряда $q$ и индуцированных зарядов на поверхности сферы.

D2  ^1.20 Найдите электростатическую энергию взаимодействия зарядов, индуцированных на поверхности сферы.

D3  ^1.00 Найдите полную электростатическую энергию взаимодействия системы.

Указание: Вы можете воспользоваться интегралом \begin{equation*} \int\limits_d^{\infty} \frac{x \, dx}{\left(x^2-R^2\right)^2} = \frac{1}{2} \frac{1}{d^2 - R^2}. \end{equation*}