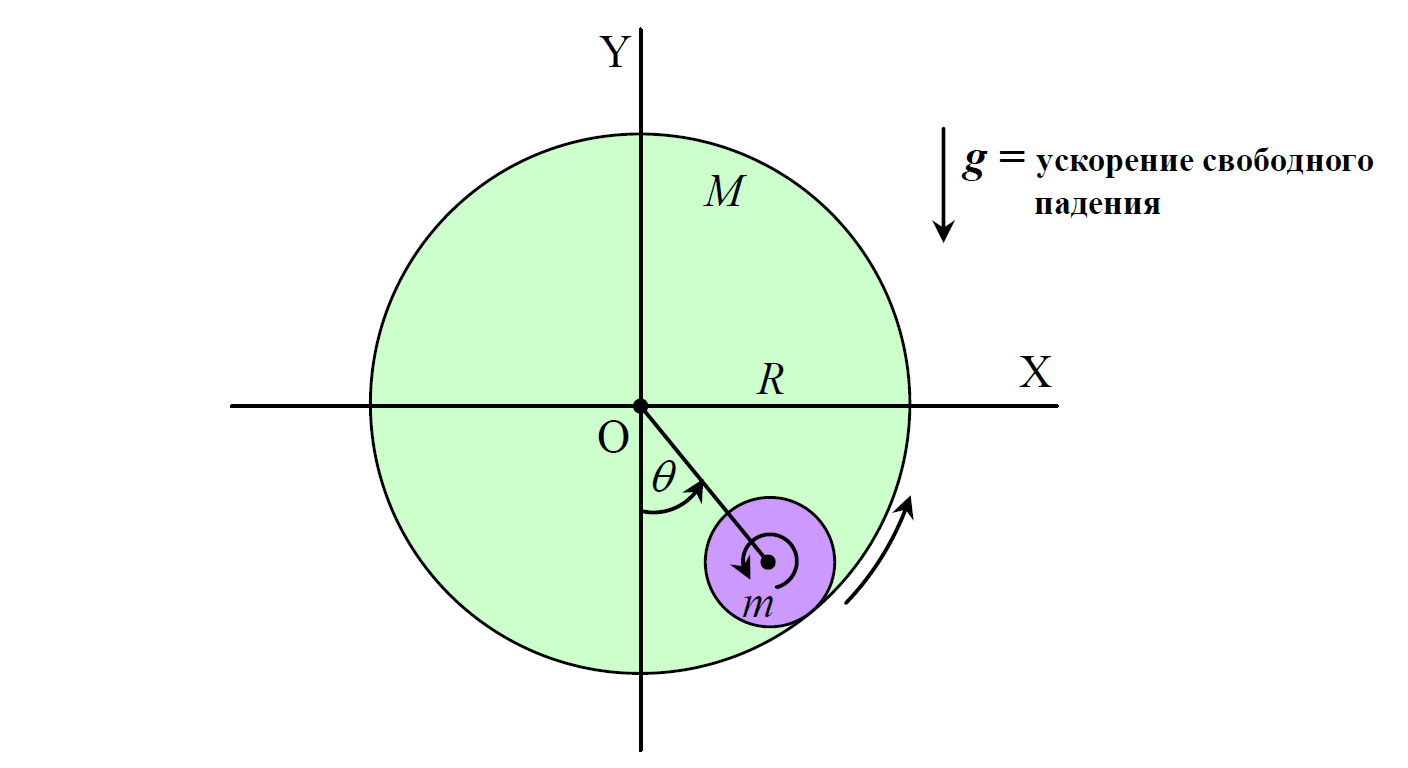
Тонкостенный цилиндр массы $M$ с шероховатой внутренней поверхностью радиуса $R$ может вращаться вокруг центральной фиксированной горизонтальной оси $OZ$. Ось $OZ$ перпендикулярна поверхности листа и направлена от нее. Другой меньший однородный сплошной цилиндр массы $m$ и радиуса $r$ катается внутри него без проскальзывания (за исключением пункта A8) по внутренней поверхности цилиндра $M$ вокруг собственной центральной оси, которая параллельна $OZ$.

A1  ^0.80 В момент времени $t=0$ цилиндр массы $M$ покоится и цилиндр массы $m$ также покоится в низшей точке. Цилиндр $M$ начинает вращаться. В некоторый момент времени $t$ угловое положение центра масс цилиндра $m$ равняется $\theta$ и при этом цилиндр $M$ совершил поворот на $\varphi$ радиан. На сколько радиан (обозначенный через $\psi$) повернулся цилиндр $m$ вокруг своей центральной оси относительной фиксированной линии (например, отрицательной части оси $Y$). Выразите ответ через $\theta$, $\varphi$, $R$ и $r$.

A2  ^0.20 Найдите угловое ускорение $\frac{d^2}{dt^2} \psi$ цилиндра $m$ относительно его центральной оси, проходящей через центр масс. Выразите ответ через $R$, $r$ и производные от $\theta$ и $\varphi$.

A3  ^1.80 Выведите уравнение для углового ускорения $\frac{d^2}{dt^2} \theta$ центра масс цилиндра $m$ относительно оси $OZ$ через $m$, $g$, $R$, $r$, $\theta$, $\frac{d^2}{dt^2} \varphi$ и момент инерции $I_{CM}$ цилиндра массы $m$ относительно его центральной оси.

A4  ^1.30 Чему равен период малых колебаний цилиндра $m$, если цилиндр $M$ вращается с постоянной угловой скоростью? Выразите ответ через $R$, $r$, $g$.

A5  ^0.20 Чему равно значение угла $\theta$ для положения равновесия цилиндра $m$ из пункта A4?

A6  ^0.70 Где находится положение равновесия цилиндра $m$, если цилиндр $M$ вращается с постоянным угловым ускорением $\alpha$? Выразите ответ через $R$, $g$, $\alpha$.

A7  ^2.50 Пусть теперь цилиндр $M$ свободно вращается (колеблется) без ограничения вокруг центральной оси $OZ$, а цилиндр $m$ совершает малые колебания, качаясь по внутренней поверхности цилиндра $M$. Найдите период этих малых колебаний.

A8  ^2.50 Рассмотрите случай когда цилиндр $M$ вращается с постоянной угловой скоростью $\Omega$, а цилиндр $m$ вращается (катается) вокруг стационарного центра масс в точке равновесия, найденного в пункте A5. Затем цилиндр $M$ мгновенно останавливают. Какое наименьшее значение должна иметь $\Omega$, чтобы цилиндр $m$ покатился и достиг высшей точки внутренней поверхности цилиндра $M$? Коэффициент трения между $m$ и $M$ предполагается достаточно большим, так что $m$ начинает катиться без проскальзывания сразу же после короткой пробуксовки после остановки цилиндра $M$.