Электролитами называют вещества, которое проводят электрический ток вследствие диссоциации на ионы. Их электропроводность обусловлена подвижностью положительно и отрицательно заряженных ионов.

Система, состоящая из ёмкости с электролитом и твердой мембраной, погруженным в него, называется электрод-электролитным интерфейсом. Такая система обладает уникальным электрическими свойствами, которые широко применяются при создании литий-ионных батарей и ионисторов (суперконденсаторов). В данной задаче мы рассмотрим основные свойства электрод-электролитного интерфейса.

В качестве электролита будет выступать раствор поваренной соли $\rm Na Cl$ в воде. В течение всей задачи будем рассматривать этот раствор, как взвесь ионов $\rm Na^+$ и $\rm Cl^-$ в жидком диэлектрике. В качестве мембраны в задаче выступает поверхность стального поршня и носика у шприца, сталь в течение всей задачи будем считать идеальным проводником, проводимость которого гораздо больше проводимости электролита.

Полезными для решения задачи могу оказаться следующие константы:

Внимание! В задаче не требуется оценка погрешностей.

Внимание! Пользуйтесь индивидуальной лампой для освещения рабочего места.

Оборудование:

1. Стальной шприц.
2. Два провода крокодил-крокодил.
3. Генератор с проводом для генератора.
4. Осциллограф с двумя осциллографическими проводами.
5. Три пластиковых контейнера.
6. Одноразовая ложка
7. Пластиковый шприц для приготовления растворов
8. Резистор $R_0=22.0~\text{Ом}$.
9. $1~\text{л}$ воды для приготовления растворов (не питьевая), бутылки отмечены синим крестиком.
10. $150~\text{г}$ соли внутри контейнера
11. Весы.
12. Линейка (из оборудования задачи E2).

Часть A. Подготовительные измерения.

A1  ^0.02 Измерьте внутренний диаметр шприца $D_0$ и расстояние $L_0$ между отметками $0~\text{мл}$ и $20~\text{мл}$.

В рамках задачи будем обозначать концентрацию раствора соли в воде безразмерной величиной $c = \dfrac{m_\text{соли}}{m_\text{воды}}$, где $m_\text{воды}$ — масса изначально взятой чистой воды, $m_\text{соли}$ — масса порошка соли, добавленного к чистой воде для получения раствора.

Приготовьте раствор соли с концентрацией $c\approx 0.07$. Наберите этот раствор в шприц, причем, чтобы избежать образования лишних пузырей внутри шприца, двигайте поршень медленно. При измерениях нужно держать шприц в каком-то фиксированном положении (например, стоящим на ножке поршня), чтобы конфигурация пузырей, которые так или иначе образуются, была одинаковой.

В течение всей задаче мы будем изучать электрические свойства раствора электролита внутри шприца, поэтому следует использовать схему, изображенную на рисунке.

Внимание! Осциллографические провода и провода генератора ни в коем случае не должны непосредственно касаться стеклянного шприца, если Вы в него уже набирали воду.

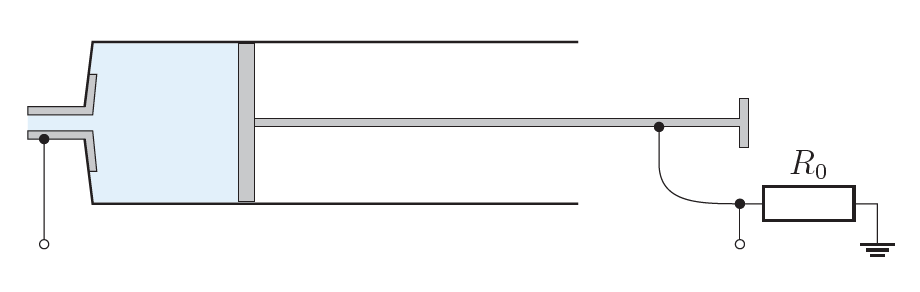
Используйте генератор в режиме $V_{\text{pp}}=1.00~\text{В}$, где $V_\text{pp}$ — разность напряжений между пиками (двойная амплитуда сигнала). Обязательно не забудьте включить сигнал на выходе генератора:

• Генератор АКИП-3408 – кнопка «Output»
• Генератор АКИП-3407 – кнопка «Выход»
• Генератор UTG2025 – кнопка «CH1» или «CH2» в зависимости от того, каким каналом Вы пользуйтесь.
• Генератор UTG9020 – автоматически включен.

Ток в нашей системе может значительно зашумлен (это т.н. электрохимический шум, который симметричен в положительную и в отрицательную область), поэтому любые амплитуды напряжений стоит измерять в режиме Cursor в ручном режиме и не полагаться на модуль Measure.

Для измерения напряжения на шприце обязательно получайте его в виде сигнала с помощью модуля Math в режиме вычитания.

Для работы с модулем Math:

1. Нажмите кнопку «Math».
2. Второй раз нажмите кнопку «Math» либо нажмите кнопку, соответствующую «РасшОпер».
3. Чтобы канал Math был равен CH1-CH2 должно быть следующее соответствие:

• «Формула» —  «A-B»
• «Действие» — «Вкл»
• «Источн.А» —  «CH1»
• «Источн.В» — «CH2»

Когда все настроено, и Вы находитесь в другом окне, например Cursor, для изменения масштаба канала Math выполните пункты 1 и 2, а затем регулируйте масштаб той же ручкой, что меняется масштаб обычных каналов (Vertical Scale).

Проверьте, что для каналов CH1 и CH2 настройка «Пробник» соответствует режиму пробника, в котором используется щуп. Если не соответствует, то настройте.

При частоте $f\approx50~\text{кГц}$ разность фаз между током через шприц и напряжением на нем практически равна нулю. Это означает, что при этой частоте раствор электролита внутри шприца ведет себя, как сопротивление $R$. Стоит ожидать, что это сопротивление меняется при изменении длины $L$ электролита внутри шприца.

A2  ^0.40 Сделайте измерения сопротивления $R$ соответствующие положениям шприца $V=2,4,\dots,20~\text{мл}$.

A3  ^0.40 Постройте график $R$ от $V$. Проведите сглаживающую прямую $R=R_1 + \alpha_1 V$. Рассчитайте значения параметров $R_1$ и $\alpha_1$.

Часть B. Объемные эффекты.

Приготовьте 4 разных раствор соли с концентрациями $0.07 \leq c \leq 0.20$. При смене концентрации раствора внутри шприца обязательно промойте его чистой водой.

B1  ^0.80 Для каждого из приготовленных растворов проведите серию из $4$-ех измерений $R$ от $V$.

B2  ^0.12 С помощью МНК для каждого из растворов посчитайте параметры $R_1$ и $\alpha_1$ по аналогии с пунктом $\textbf{А3}$. Результаты представьте в виде таблицы.

Теоретическое описание полученных результатов следует из стандартной задачи проводимости второго рода: рассмотрим действие электрического поля на заряженную частицу в вязкой среде. Пусть масса частицы $m$, а заряд $q$, а если частица движется, то на нее действует сила вязкого трения $F=-kv$.

B3  ^0.06 В среде создается внешнее постоянное поле $E$. Чему равна установившаяся скорость частицы $v_{у}$? Ответ запишите через $E,k,q$.

Коэффициент вязкости $k$, с помощью которого мы моделируем движение ионов в растворе связан не только с вязкостью, но и с электрическими свойствами воды и зависит от концентрацией ионов:
\[ k \propto n^{\alpha}, \]
где $\alpha$ — неизвестная степень, одинаковая для ионов $\rm Na^+$ и $\rm Cl^-$.

Пусть электронейтральный раствор поваренной соли находится внутри цилиндрического сосуда с проводящими основаниями-электродами и непроводящими стенками. Площадь оснований $S$, расстояние между ними $L$. Будем считать, что ионы $\rm Na^+$ и $\rm Cl^-$ в любом количестве могут возникать и пропадать в результате химических реакций с электродами. Заряды ионов по модулю совпадают с элементарным зарядом $e=1.602\cdot10^{-19}~\text{Кл}$.

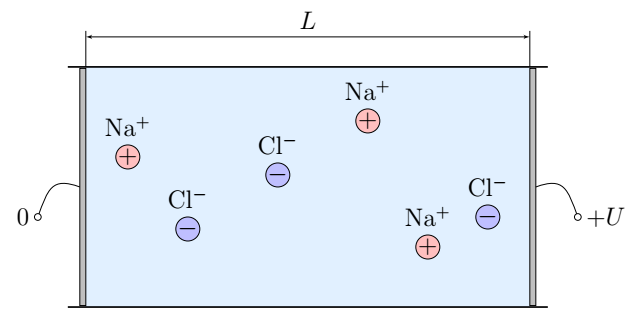
Обозначим за $n$ концентрацию ионов натрия, за $k_{\rm Na^+}$ и $k_{\rm Cl^-}$ — коэффциенты взякости для ионов натрия и хлора соотвественно.

B4  ^0.15 Чему равен установившийся ток $I$, если к электродам подведена разность потенциалов $U$? Любыми поверхностными эффектами пренебрегите (например, контактной разностью потенциалов и контактным сопротивлением). Ответ запишите через $n,S,L,e,k_{\rm Na^+}, k_{\rm Cl^-}$ и $U$.

На практике исследование постоянного тока сопряжено со следующей трудностью: из-за химических реакций постепенно разрушаются/покрываются пленкой основания цилиндра. Поэтому значительно удобнее исследовать проводимость при переменном токе. Проведем теоретический анализ в рамках нашей модели.

B5  ^0.65 Пусть к основаниям подведена разность потенциалов $U(t) = U \cos \omega t$, как будет зависеть ток $I(t)$ от времени? Любыми поверхностными эффектами снова пренебрегите. Ответ запишите через $n,S,L,e,\omega,m_{\rm Na^+}, m_{\rm Cl^-},k_{\rm Na^+}, k_{\rm Cl^-}, U$ и $t$.

B6  ^0.25 Теперь учтем поверхностные эффекты в виде резистора $R_\text{п}$, который последовательно подключен к раствору. Запишите формулу для импеданса $\tilde{Z}(\omega)$ системы, состоящей из раствора $\rm NaCl$ и сосуда. Ответ запишите через $n,S,L,e,m_{\rm Na^+}, m_{\rm Cl^-},\omega,k_{\rm Na^+}, k_{\rm Cl^-}$ и $R_\text{п}$.

B7  ^0.10 Чему равен теоретический импеданс системы $\tilde{Z}$, если разность фаз между напряжением пренебрежимо мала? Ответ выразите через $n,S,L,e,k_{\rm Na^+}, k_{\rm Cl^-}$ и $R_\text{п}$.

Случаю, рассмотренному в $\textbf{B8}$ очевидно соответствуют измерения, сделанные в рамках пунктов $\textbf{A2}$ и $\textbf{B1}$.

B8  ^0.40 Используя линеаризованный график $\alpha_1$ от $c$ получите значение $\alpha$.

B9  ^0.40 Получите теоретическую зависимость $|\tilde{Z}|^2(\omega)$ в приближении $\omega m_{\rm Na^+} \gg k_{\rm Na^+}$, $\omega m_{\rm Cl^-} \gg k_{\rm Cl^-}$. Ответ запишите через $n,S,L,e,m_{\rm Na^+}, m_{\rm Cl^-},\omega,k_{\rm Na^+}, k_{\rm Cl^-}$ и $R_\text{п}$.

B10  ^0.35 Для раствора с концентрацией соли $c\approx 0.20$ проведите измерения модуля импеданса $|Z|$ от частоты $f$. Серия должна состоять из не менее 7-ми разных $f$ в диапазоне $500~\text{кГц} \leq f \leq 10~\text{МГц}$.

B11  ^0.50 Постройте линеаризованный график $|Z|$ от $f$. Из графика определите экспериментальное значение $\mu_\text{эфф}=\frac{\mu_{\rm Na} \cdot \mu_{\rm Cl}}{\mu_{\rm Na} + \mu_{\rm Cl}}$.

Полученное в эксперименте $\mu_\text{эфф}$ значительно отличается от теоретического значения. Это отличие можно объяснить тем, что молекулы воды, которые обладают дипольным моментом, притягиваются к ионам (сольватируют их) и двигаются вместе с ними. Обозначим, количество молекул воды, двигающихся вместе с ионом любого вида за $N$.

В таком случае вместо $\mu_{\rm Na}$ при расчете нужно использовать $\mu_{\rm Na}+N\mu_{H_2O}$ и вместо $\mu_{\rm Cl}$ нужно использоваться $\mu_{\rm Cl} + N \mu_{H_2O}$

B12  ^0.15 Определите $N$ исходя из ваших экспериментальных данных.

Часть С. Поверхностные эффекты.

Шприц с электролитом также обладает ёмкостью, которую невозможно предсказать в рамках теории объемных эффектов. Эта ёмкость начинает сказываться при малых частотах сигнала, подаваемого на концы шприца.

Ёмкость системы поверхность электрода-электролит связана с тем, что ионы(как и любые заряженые частицы) притягиваются к поверхности металла и формируют т.н. двойной электрический слой. Таким образом единица поверхности соприкосновения металла с электролитом обладает ёмкостью $\sigma = \frac{dC}{dS}$, где $C$ — ёмкость поверхности площадью $S$.

Наполните шприц раствором с концентрацией соли $c\approx 0.20$.

C1  ^1.50 В диапазоне частот $5~\text{Гц} \leq f \leq 1~\text{кГц}$ проведите измерения модуля импеданса шприца $|\tilde{Z}|$ и времени $\Delta t$, на которое пик тока опережает пик напряжения. Сделайте не менее 15 измерений.

Для анализа электрической схемы бывает полезна т.н. диаграмма Найквиста — зависимость $\mathfrak{Im} \tilde{Z}$ от $\mathfrak{Re} \tilde{Z}$.

В нашем случае можно считать, что объемные эффекты сводятся к резистору сопротивлением $R_2$, а поверхностные выражаются из измерений следующим образом: $\tilde{Z}_\text{п} = \tilde{Z} - R_2$.

C2  ^0.60 На основе Ваших данных постройте диаграмму Найквиста $\mathfrak{Im} \tilde{Z}_\text{п}$ от $\mathfrak{Re} \tilde{Z}_\text{п}$ для поверхностных эффектов. Укажите на диаграмме в виде стрелки направление перехода от точки к точке, соответствующее увеличению $\omega$.

C3  ^0.10 Качественно изобразите диаграмму Найквиста для плоского конденсатора.

Описанная ранее модель формирования ёмкости $C$ у поверхности соприкосновения электролита и металла в случае, если эта поверхность плоская, должна сводится к тому, что поверхностные эффекты имеют диаграмму Найквиста, как у конденсатора, но эксперимент противоречит этому тезису. При анализе схожей задачи датским химиком Робертом де Леви была предложена модель шероховатой поверхности металла, которая оказалась очень плодотворной для описания электрических свойств электрод-электролитных интерфейсов.

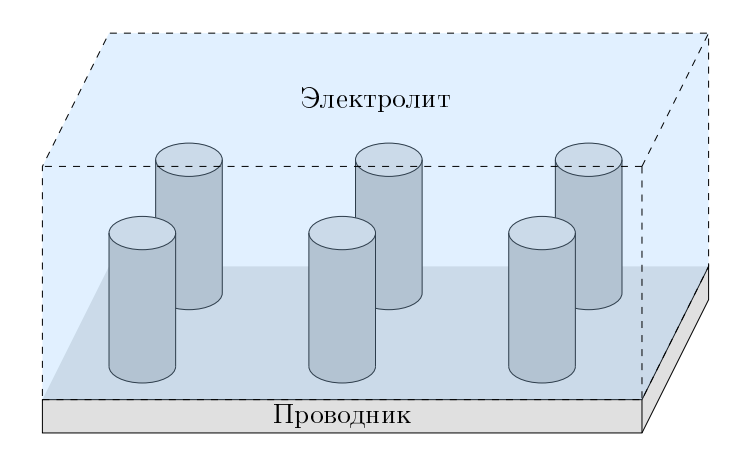
Представим поверхность проводника, как плоскость, на которой стоят цилиндры высоты $l$ и радиуса $r$. Плотность постановки цилиндров можно описать поверхностной плотностью $\xi = \frac{dN}{dS}$, где $N$ — число цилиндров на площади $S$.

В таком случае на один цилиндр приходится $1/\xi$ площади электролита вокруг него. При этом единица высоты цилиндра обладает некоторой ёмкостью $C_l$ и единица высоты электролита, приходящегося на один цилиндр, обладает некоторым сопротивлением $R_l$. Для сокращения записей обозначим за $\rho$ удельное сопротивление электролита.

C4  ^0.20 Запишите выражения для $C_l$ и $R_l$ через $r,\sigma,\rho$ и $\xi$.

C5  ^0.10 Запишите комплексный ток $\tilde{I}(x)$ через производную комплексного потенциала $\frac{d\tilde{\varphi}(x)}{dx}$ и $R_l$.

C6  ^0.10 Свяжите производную комплексного тока $\frac{d\tilde{I}(x)}{dx}$ и комплексный потенциал $\tilde{\varphi}(x)$ через $C_l$.

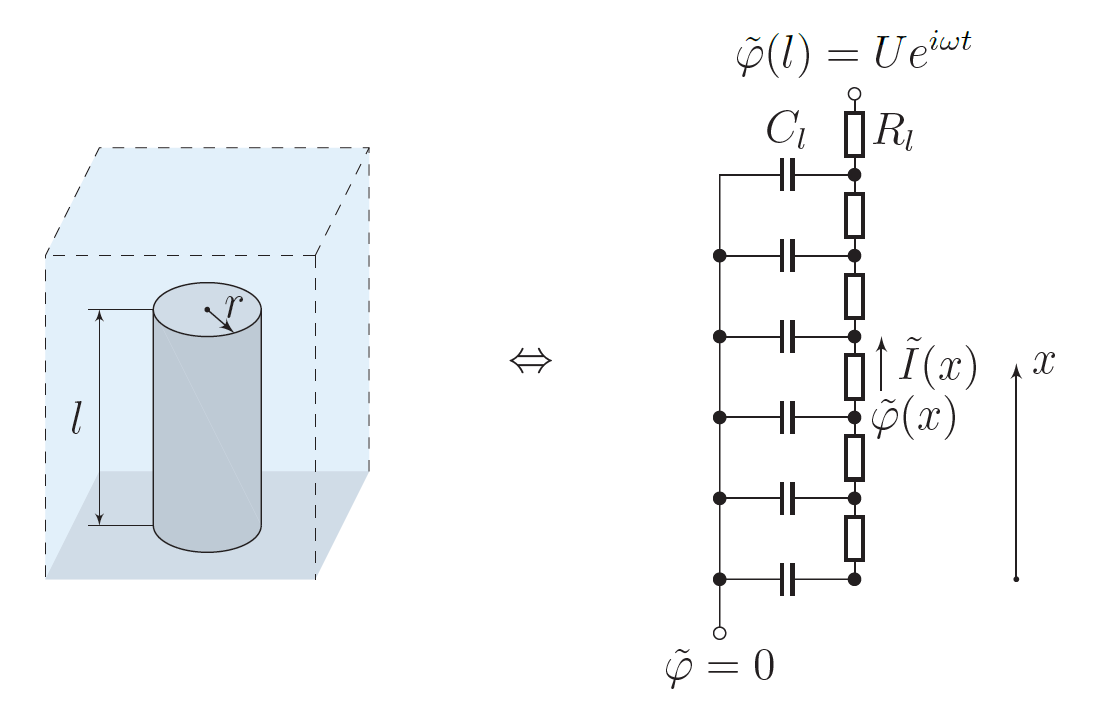
Примечание 1: для нахождения двух чисел $a$ таких, что $a^2=\sqrt{i}$ можно воспользоваться формулой Эйлера.

Примечание 2: $\cos x = \cosh ix$, $i \sin x = \sinh ix$, $i \tan x = \tanh ix$, $\tanh(x \pm y) = \dfrac{\tanh x \pm \tanh y}{1 \pm \tanh x \tanh y}$.

C7  ^0.20 Покажите, что $\tilde{I}(0) = 0$.

C8  ^1.25 Решите полученную в пунктах $\textbf{C5}$ и $\textbf{C6}$ систему дифференциальных уравнений и получите импеданс $\tilde{Z}_\text{ц}(\omega)$ одного цилиндра и электролита, окружающего его. Ёмкостью основания цилиндра и ёмкостью плоской поверхности, на которой стоят цилиндры пренебрегайте. Ответ выразите через $C_l,R_l,l$ и $\omega$.

C9  ^0.20 Получите импеданс $\tilde{Z}_\text{ц}(\omega)$ в приближении $\sqrt{\omega C_l R_l l^2} \gg 1$. Ответ выразите через $C_l,R_l,l$ и $\omega$. Следующие теоретические пункты также решаются в этом приближении.

C10  ^0.20 Чему равен импеданс $\tilde{Z}_\text{п}(\omega)$ одной поверхности цилиндра, соприкасающейся с электролитом. Площадь поверхности $S$. Ответ выразите через $r,\sigma,\rho,\xi,S$ и $\omega$.

Нарисуйте качественно диаграмму Найквиста $\tilde{Z}_\text{п}(\omega)$. Теоретическая и экспериментальная диаграммы Найквиста должны совпадать по форме, но часть их характеристик могут незначительно отличаться.

С11  ^0.70 Постройте линеаризованный график $|\tilde{Z}_\text{п}|$ от $\omega$.

Будем считать, что $\xi=40~\frac{1}{\text{мм}^2}$, $r=0.6~\text{мкм}$. Площадь контакта носика шприца с электролитом считайте в $5.5$ раз меньше площади внутреннего сечения шприца.

C12  ^0.10 Определите $\sigma$.