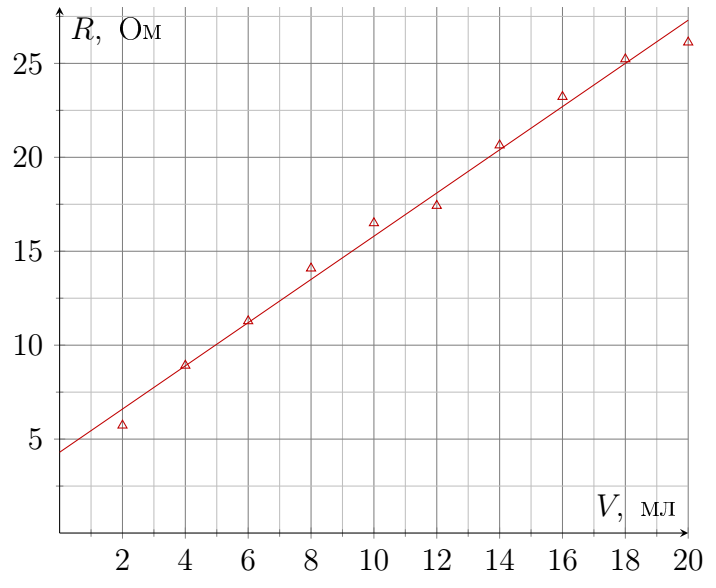
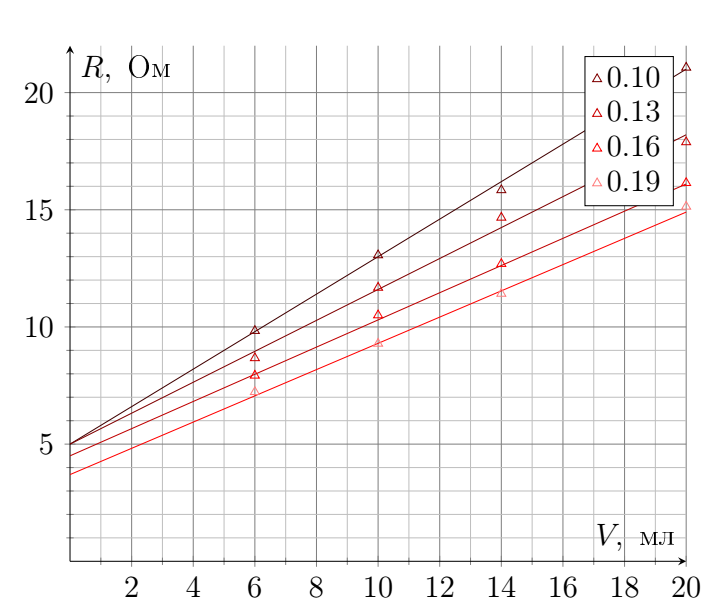
c 0.07 0,1 0,13 0,16 0,19 $\alpha_1,~\frac{\text{Ом}}{см^3}$ 1.15 0.80 0.66 0.58 0.56 $R_1,~\text{Ом}$ 4.3 5.0 4.9 4.5 3.7
Запишем II закон Ньютона:
\[ Eq = kv_\text{y} \]
По определению $I = \frac{dq}{dt}$, при этом поток площадью $S$ частиц зарядом $q$, двигающийся с постоянной скоростью $v$ образует такой ток:
\[ I = \frac{dq}{dt}= nvSq \tag{1}\]
Тогда ток в нашем случае складывается из двух потоков ионов. Концентрации ионов равны из условия электронейтральности:
\[ I = nSe \frac{Ee}{k_{\rm Na^+}} + nSe \frac{Ee}{k_{\rm Cl^-}}.\]
Поле $E$ выражается через разность потенциалов, как $U/L$.
Будем решать задачу методом комплексных амплитуд:
\[ U \cos \omega t = \mathfrak{Re} \, U e^{i \omega t}. \]
Тогда комплексное электрическое поле $E$ внутри среды такое:
\[ \tilde{E} = \frac{U}{L} e^{i \omega t}. \]
Запишем II закон Ньютона для частицы в переменном поле $Ee^{i\omega t}$:
\[ m\dot{v} + kv = Eq e^{i \omega t}.\]
Собственные решения являются экспоненциально спадающими, поэтому нас интересует только частное решение вида $v=\tilde{B} e^{i \omega t}$:
\[ i\omega m \tilde{B} + k\tilde{B} = Eq \quad \Rightarrow \quad \tilde{B} = \frac{Eq}{i \omega m + k} = \frac{Eq}{k} \frac{1}{1 + i\omega\frac{m}{k}} = \frac{Eq}{k} \frac{1}{\sqrt{1+\frac{\omega^2 m^2}{k^2} }}e^{-i\arctan \frac{\omega m}{k}}.\]
Комплексный ток $\tilde{I}$ пересчитаем c учетом уравнения (1):
\[ \tilde{I} = \frac{nSe^2 U}{Lk_{\rm Na^+}} \frac{1}{\sqrt{1+\frac{\omega^2 m_{\rm Na^+}^2}{k_{\rm Na^+}^2} }} e^{-i\arctan \frac{\omega m_{\rm Na^+}}{k_{\rm Na^+}} +i \omega t} + \frac{nSe^2 U}{Lk_{\rm Cl^-}} \frac{1}{\sqrt{1+\frac{\omega^2 m_{\rm Cl^-}^2}{k_{\rm Cl^-}^2} }} e^{-i\arctan \frac{\omega m_{\rm Cl^-}}{k_{\rm Cl^-}}+i \omega t}\]
Перейдем от комплексного тока путем взятия действительной части.
Импеданс одного вида ионов очевидно выражается из уже полученных уравнений
\[ \tilde{Z} = \frac{Lk}{nSq^2} \left( 1+ i \omega \frac{m}{k} \right),\]
при этом токи складываются при одинаковых напряжениях, значит импедансы $\rm Na^+$ и $\rm Cl^-$ "подключены" параллельно, и еще последовательно с ними стоит резистор $R_\text{п}$.
Если разность фаз пренебрежимо мала, то комплексными частями можно пренебречь и поведение системы соответствует поведению при постоянном напряжении.
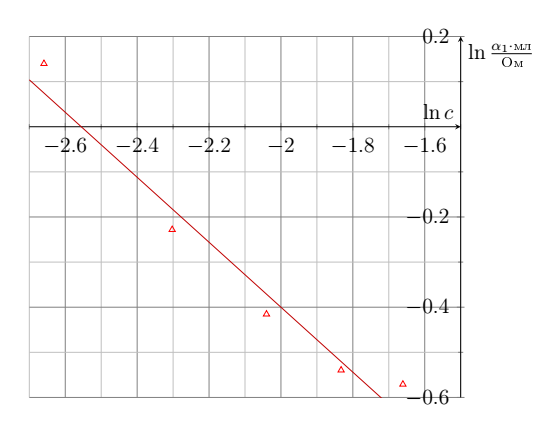
Упростим формулу для импеданса из B6:
\[ \tilde{Z} = R_\text{п} + \frac{L}{nSe^2} \frac{(k_{\rm Na^+} + i \omega m_{\rm Na^+})(k_{\rm Cl^-} + i \omega m_{\rm Cl^-})}{(k_{\rm Na^+} + k_{\rm Cl^-}) + i \omega (m_{\rm Na^+}+m_{\rm Cl^-})} \]
Первое приближение происходит на этапе перемножения:
\[ \tilde{Z} = R_\text{п} + \frac{L}{nSe^2} \frac{
-\omega^2 m_{\rm Na^+} m_{\rm Cl^-}+ i \omega( m_{\rm Na^+}k_{\rm Cl^-} +m_{\rm Cl^-}k_{\rm Na^+})
}{(k_{\rm Na^+} + k_{\rm Cl^-}) + i \omega (m_{\rm Na^+}+m_{\rm Cl^-})} \]
Домножим числитель и знаменатель на комплексно сопряженное к знаменателю и снова сделаем пренебрежение:
\[ \tilde{Z} = R_\text{п} + \frac{L}{nSe^2} \frac{
- \omega^2 m_{\rm Na^+} m_{\rm Cl^-} (k_{\rm Na^+} + k_{\rm Cl^-})+ i\omega^3 m_{\rm Na^+} m_{\rm Cl^-} ( m_{\rm Na^+} + m_{\rm Cl^-}) + \omega^2 ( m_{\rm Na^+}k_{\rm Cl^-} +m_{\rm Cl^-}k_{\rm Na^+}) (m_{\rm Na^+} + m_{\rm Cl^-})
}{
\omega ^2(m_{\rm Na^+}+m_{\rm Cl^-})^2}
\]
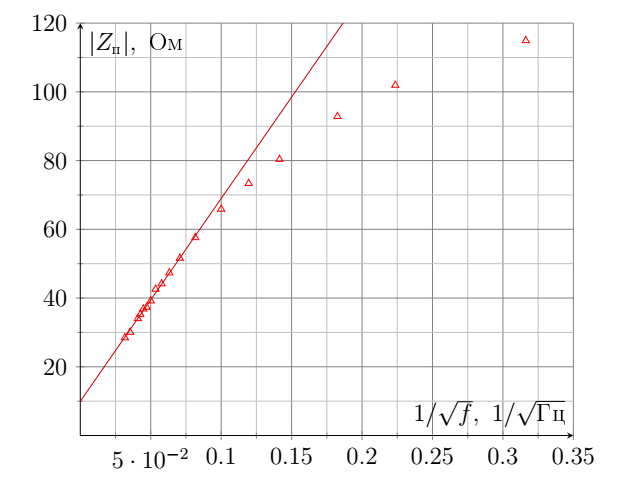
Согласно последнему теоретическому пункту график $|\tilde{Z}|^2$ от $f^2$ линейный.
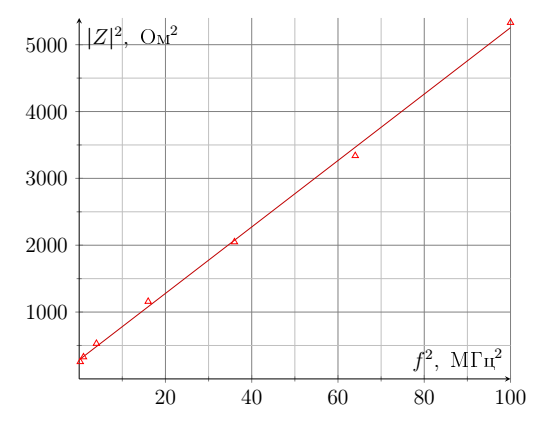
Запишем формулу исходя из модели, описанной в условии:
\[ \mu_\text{эфф} = \frac{(\mu_{\rm Na}+ N \mu_{\rm H_2 O})\cdot (\mu_{\rm Cl}+ N \mu_{\rm H_2 O})}{\mu_{\rm Na}+ N \mu_{\rm H_2 O} + \mu_{\rm Cl}+ N \mu_{\rm H_2 O}}\]
Преобразуем к квадратному уравнению относительно $N$:
\[ N^2 + N \left( \frac{\mu_{\rm Na}+\mu_{\rm Cl}- 2 \mu_\text{эфф} }{\mu_{\rm H_2O}} \right) + \frac{\mu_{\rm Na}\mu_{\rm Cl} - \mu_\text{эфф} (\mu_{\rm Na} + \mu_{\rm Cl})}{\mu_{\rm H_2O}^2}=0\]
Из-за того, что $\mu_\text{эфф}$ очень больше, фактически, $N=\frac{2\mu_\text{эфф}}{\mu_{\rm H_2O}}=1.8\cdot 10^{7}$.
Можно заключить, что измеренная индуктивность никак не связана с теоретически рассмотренным эффектом. Тем временем индуктивность витка с током радиусом $10~\text{см}$ можно оценить, как $10^{-6}~\text{Гн}$, что имеет один порядок с корнем из коэффициента наклона.
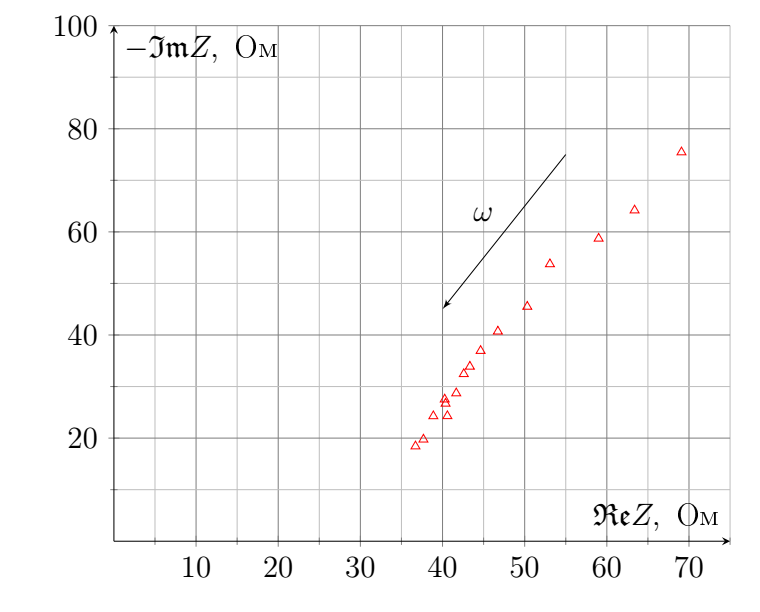
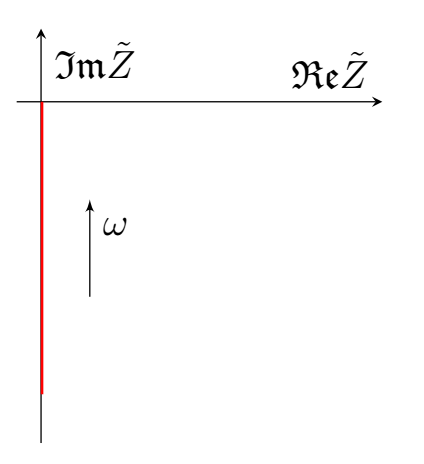
Запишем падение напряжения на единице длины проводника:
\[ -R_ldx \, \tilde{I} = \tilde{\varphi}(x+dx) - \tilde{\varphi}(x) \]
Ток через единицу длины конденсатора
\[ \frac{\tilde{I}(x+dx) - \tilde{I}(x)}{i\omega C_l dx} = -\tilde{\varphi} (x) \]
Если ток не нулевой, то он течет через бесконечно малую ёмкость, значит $\varphi(0) \to \infty$.
Получим дифференциальное уравнение на $\tilde{\varphi}(x)$:
\[ \tilde{\varphi}'' - i \omega C_l R_l \tilde{\varphi} = 0 \]
Это однородное линейное диф.уравнение второго порядка. Найдем собственные числа:
\[ \lambda^2 = i \omega C_l R_l. \]
\[ \lambda_1 = e^{\frac{i \frac{\pi}{2}}{2}} \sqrt{\omega C_l R_l} = (1+i) \sqrt{\frac{\omega R_l C_l}{2}} \]
\[ \lambda_2 = e^{\frac{i \frac{\pi}{2}+2\pi i}{2}} \sqrt{\omega C_l R_l} = -(1+i) \sqrt{\frac{\omega R_l C_l}{2}} \]
Обозначим $\sqrt{\frac{\omega C_l R_l}{2}}$ за $\zeta$. Тогда
\[ \tilde{\varphi}(x) = A e^{i \zeta x} e^{\zeta x} + B e^{-i \zeta x} e^{-\zeta x}.\]
Граничные условия: $\tilde{\varphi}(l)=Ue^{i \omega t}$, $\tilde{\varphi}'(0) = 0$.
\[ \tilde{\varphi}'(0) = A(1+i) \zeta - B(1+i)\zeta = 0 \quad \Rightarrow \quad B = A,\]
\[ \tilde{\varphi}(l) = A \left( e^{i \zeta l} e^{\zeta l} + e^{-i \zeta l} e^{-\zeta l} \right) = 2A \cosh(\zeta l + i \zeta l) = U e^{i \omega t} \]
В итоге решение на потенциал выглядит так:
\[ \tilde{\varphi}(x) = U e^{i \omega t} \frac{ \cosh(\zeta x+i \zeta x)}{\cosh(\zeta l+ i \zeta l)}\]
Найдем ток $\tilde{I}(l)$:
\[ \tilde{I}(l) = -\frac{1}{R_l} \tilde{\varphi}'(l) = -U e^{i \omega t} \frac{\zeta (1+i)}{R_l} \tanh(\zeta l+ i \zeta l), \]
затем импеданс (минус возникает благодаря согласованию положительного направления ток и убывания импеданса):
\[\tilde{Z}_\text{ц} = \frac{\tilde{\varphi}(l)}{-\tilde{I}(l)}= \frac{R_l}{\zeta (1+i) \tanh (\zeta l + i \zeta l) } = \sqrt{\frac{R_l}{2\omega C_l}} \frac{1-i}{\tanh \left( (1+i) \sqrt{\frac{\omega C_l R_l}{2}} l \right)} \]
Разложим $\tanh$:
\[\tilde{Z}_\text{ц} = \sqrt{\frac{R_l}{\omega C_l}} \frac{1 - i\tanh \sqrt{\frac{\omega C_l R_l}{2}} l \cdot \tan \sqrt{\frac{\omega C_l R_l}{2}} l}{\tanh \sqrt{\frac{\omega C_l R_l}{2}} l - i\tan \sqrt{\frac{\omega C_l R_l}{2}} l} e^{-i\pi/4}. \]
Домножим числитель и знаменатель на $\cosh \zeta l \cdot \cos \zeta l$:
\[\tilde{Z}_\text{ц} = \sqrt{\frac{R_l}{\omega C_l}}
\frac{\cosh \zeta l \cos \zeta l + i \sin \zeta l \sinh \zeta l}
{\cos \zeta l \sinh \zeta l + i \cosh \zeta l \sin \zeta l}
e^{-i\pi/4}, \]
при $\zeta l \gg 1$ гиперболические функции $\sinh \zeta l$ и $\cosh \zeta l$ равны экспоненте $\frac{e^{\zeta l}}{2}$, поэтому
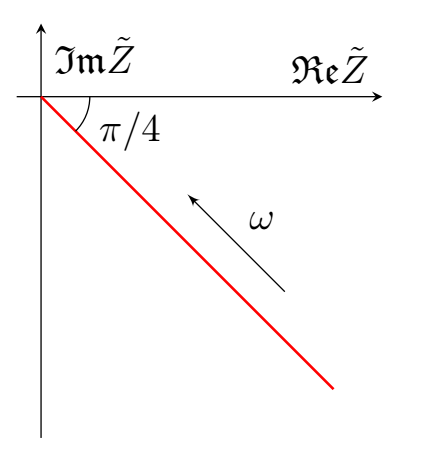
\[ \tilde{Z}_\text{ц} \simeq \sqrt{\frac{R_l}{\omega C_l}} \frac{\cos \zeta l e^{\zeta l} + i \sin \zeta l e^{\zeta l}}{\cos \zeta l e^{\zeta l} + i \sin \zeta l e^{\zeta l}}e^{-i\pi/4} = \sqrt{\frac{R_l}{\omega C_l}}e^{-i\pi/4} \]
Совместим результаты предыдущих пунктов.
\[ \tilde{Z}_\text{п} = \frac{1}{\xi S}
\sqrt{
\frac{\rho}{2\pi r \sigma \omega \left(\frac{1}{\xi} - \pi r^2 \right)}
} e^{-i\pi/4}\]