
Гироскопические силы являются причинами ряда интересных явлений. Например, сила Кориолиса приводит к размыванию берегов рек, сила Лоренца приводит к искривлению траекторий движения частиц, к прецессии атомов в магнитном поле и т.д.
Помимо гироскопических сил, интересными для изучения являются паразитные виды трения — трение качения и трения верчения, возникающие при качении и верчении тел на поверхности.
В данной задаче также изучается влияние магнитного поля и паразитных видов трения на механическое движение.
Как известно, момент сил, действующих на виток с током со стороны однородного магнитного поля, не равен нулю. Рассмотрим шар радиусом $r$ с неподвижным центром, заряженный равномерно по объёму зарядом $q$ и вращающийся с угловой скоростью $\vec{\omega}$ в однородном магнитном поле с индукцией $\vec{B}$. Вращающийся шар эквивалентен набору круговых токов.
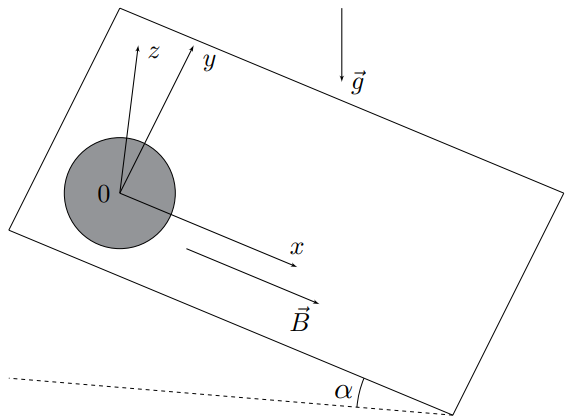
На приведённом рисунке показана система координат $xyz$ c единичными ортами $\vec{e}_x$, $\vec{e}_y$ и $\vec{e}_z$ такими, что орт $\vec{e}_y$ направлен горизонтально, а вектор индукции магнитного поля записывается как $\vec{B}=\vec{e}_x\cdot{B}$.
Введём обозначения:
В момент времени $t=0$ шар неподвижен, а его центр расположен в начале координат.
B1
0.50
Запишите условие отсутствия проскальзывания шара по плоскости через $\vec{v}_C$, $\vec{\omega}$ и $\vec{r}$. Используя полученное выражение, выразите компоненты угловой скорости $\omega_x$ и $\omega_y$ через $v_{Cx}$, $v_{Cy}$ и $r$.
Дифференцируя по времени условие отсутствия проскальзывания, выразите $\vec{a}_C$ через $\dot{\vec{\omega}}$ и $\vec{r}$.
Поскольку момент инерции $I$ шара одинаков для любой оси, проходящей через центр, вектор его момента импульса относительно центра масс записывается в виде:
$$\vec{L}_C=I\vec{\omega}
$$
B3 0.20 Выразите силу трения $\vec{F}$ через $m$, $q$, $\vec{B}$, $\vec{\omega}$, $\vec{r}$ и $\vec{a}_C$.
Примечание: Воспользуйтесь свойством двойного векторного произведения:
$$\bigl[\vec{a}\times\bigl[\vec{b}\times\vec{c}\bigr]\bigr]=\vec{b}\bigl({~}\vec{a}\cdot\vec{c}{~}\bigr)-\vec{c}\bigl({~}\vec{a}\cdot\vec{b}{~}\bigr)$$
Из уравнения динамики вращательного движения видно, что при движении шар начинает вертеться (вращаться относительно оси $z$, перпендикулярной плоскости).
Перейдём к анализу траектории центра шара. Далее во всех пунктах изначально шар неподвижен, а его центр расположен в начале координат.
Проанализируем кинематику данного движения.
B8
0.50
Опишите эволюцию угловой скорости шара $\vec{\omega}$. В качестве ответ укажите годограф вектора угловой скорости (в системе координат $xyz$), т.е кривой, описывающей положения конца вектора при его фиксированном начале. Укажите на рисунке все характерные значения. Выразите их через $m$, $g$, $q$, $B$, $\alpha$ и $r$.
Перейдём к необходимым условиям движения шара без проскальзывания.
В действительности, на движение шара влияют сразу два вида паразитного трения - трение качения и трение верчения. В двух следующих частях независимо изучаются влияния данных эффектов на движение шара.
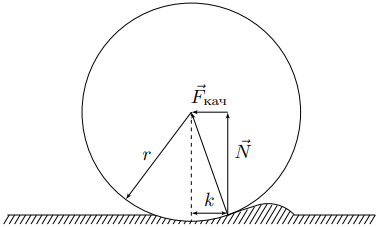
В момент времени $t=0$ шар неподвижен, а его центр расположен в начале координат.
Далее считайте, что $\operatorname{tg}\alpha\gg{k/r}$.
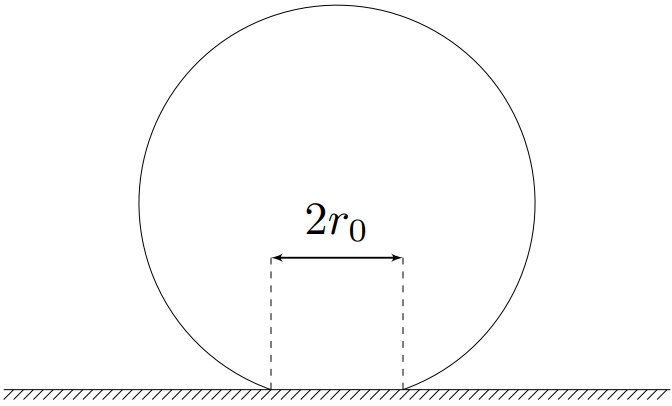
Примечание 1: Вообще говоря, величина $r_0$ определяется силой нормальной реакции $N$, но при решении задачи находить связь $r_0$ и $N$ не нужно.
Примечание 2: В данной части задачи под отсутствием проскальзывания подразумевается, что центр круга соприкосновения шара и плоскости всегда неподвижен. Считайте, что сила трения покоя приложена к к центру круга соприкосновения.
В момент времени $t=0$ шар неподвижен, а его центр расположен в начале координат.