
Во всех пунктах задачи считайте, что компонента индукции $B_z$ магнитного поля внутри сердечника зависит только от координаты $z$. Также везде, кроме части C, считайте, что ЭДС индукции в кольце вызвана только вихревым электрическим полем.
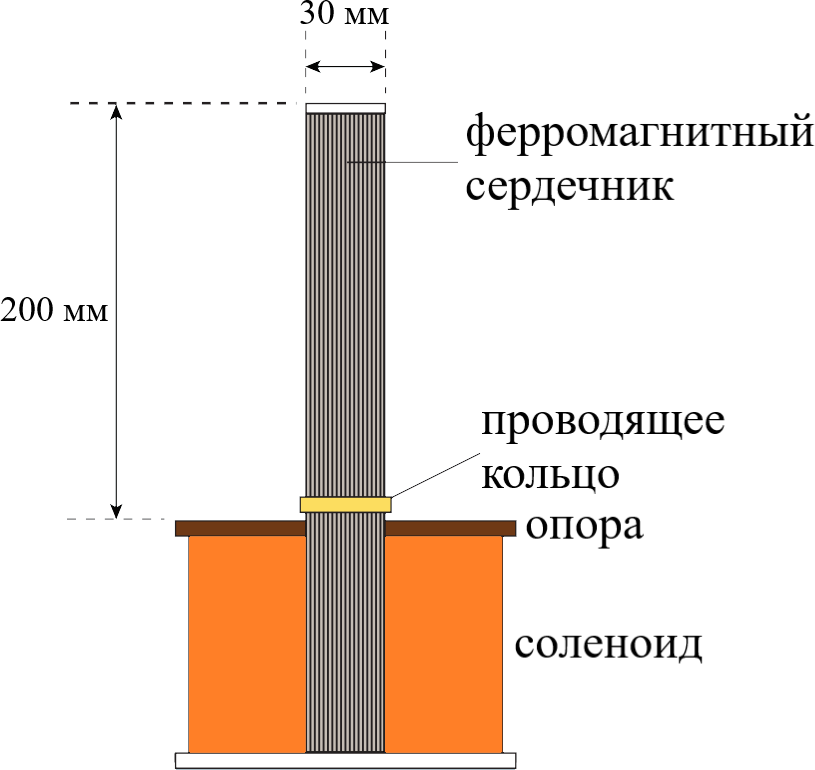
Рассмотрим движение кольца вдоль сердечника. Введём цилиндрические координаты, направив ось $z$ вертикально вверх вдоль оси симметрии сердечника так, что опора соответствует координате $z=0$. Пусть внутри сердечника аксиальная компонента магнитного поля равна $B_z(t)$, снаружи сердечника радиальная компонента магнитного поля равна $B_\rho(t)$. При изменении магнитного поля в сердечнике в кольце возникают токи Фуко, которые взаимодействуют с радиальной компонентой магнитного поля. За положительное направление токов примите направление обхода против часовой при виде сверху.
Пусть теперь компоненты поля будут функциями не только времени $t$, но и координаты $z$. Будем однако считать, что характерный масштаб, на котором эти функции заметно изменяются, намного больше масштаба «быстрых» колебаний кольца. Таким образом, $B_z(z,t)=B_{0z}(z)\cos\omega t$ и $B_\rho(z,t)=B_{0\rho}(z)\cos\omega t$.
Поскольку частота $\omega$ переменного тока также заметно больше характерного масштаба времени, на котором происходит движение кольца, можно считать, что на кольцо действует сила $F_z(z)$, усреднённая по периоду.
Расчёт компонент магнитного поля в реальном индукционном ускорителе — довольно сложна задача, поэтому далее в будем считать, что $B_{0z}(z)$ убывает линейно от некоторого значения $B_0$ при $z=0$ до нуля при $z=H$. Выше верхнего края сердечника поле отсутствует.
Эти величины можно связать между собой.
В этой части учтём вклад в ЭДС, вызванный изменением магнитного потока в кольце вследствие его движения вдоль оси $z$. Предположим, что мы включили магнитное поле резко, и кольцо подлетело на высоту $h_\mathrm m=16~см$. В дальнейшем кольцо совершает периодическое движение вдоль сердечника, медленно теряя энергию за счёт диссипации, вызванной этим вкладом в ЭДС. Исследуем это движение.
Пусть кольцо движется в точке $z$ со средней скоростью $v_z$.
Из-за вышеописанных потерь в результате каждого колебания амплитуда колебаний кольца $A$ будет уменьшаться на некоторую величину $\Delta A\ll A$. Введём логарифмический декремент затухания как $\delta=\Delta A/A$.
Подадим теперь на соленоид ровно такой ток, чтобы кольцо перестало давить на опору. Положим сверху ещё одно такое же кольцо. Вопреки интуиции пара колец поднимется над опорой на некоторую высоту. Исследуем это явление подробнее.
D1
0.80
Найдите сопротивление $R_n$ стопки из $n$ контактирующих колец. Найдите удельную силу $F_n/nmg$, действующую на каждое из колец в стопке при $z=0$. На какой высоте $h_n$ при этом левитирует стопка? Кольца можно считать очень тонкими, поэтому индуктивность стопки колец равна индуктивности одного кольца. Ответы выразите через $n$, $H$, $R$, $L$, $\omega$.
Индукционный ускоритель Томсона можно рассматривать не только как интересную демонстрационную модель, но и как вполне рабочий преобразователь электрической энергии в механическую. Попробуем выяснить, насколько он эффективен. Параметры установки для численного расчёта те же, что и во введении; $h=18~см$. Считайте, что при резком включении поля кольцо способно подняться выше верхнего края сердечника.