Фотонные кристаллы являются материалами, показатель преломления которых периодически изменяется на масштабах, сравнимых с длиной волны света. В оптическом спектре фотонных кристаллов существуют узкие области длин волн, для которых распространение света подавляется. Эти необычные оптические свойства используются для создания разнообразных оптических элементов на основе фотонных кристаллов (оптических фильтров, отражателей).
В данной работе вам предлагается изучить свойства фотонных кристаллов на примере пористых (содержащих воздушные каналы) пленок оксида алюминия. Структура образцов, полученных с помощью электрохимического окисления (анодирования) алюминия, может быть представлена как система несвязанных цилиндрических каналов, расположенных перпендикулярно поверхности образца (см. рис).
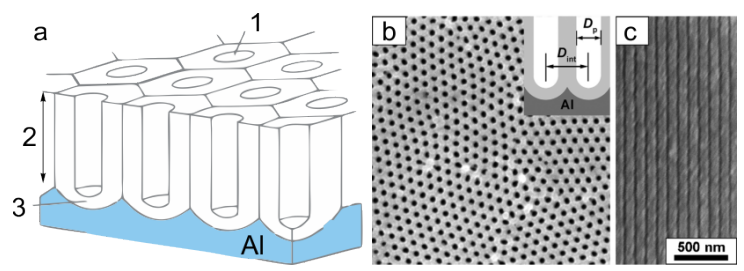
Диаметр пор и расстояние между ними зависят от условий электрохимической обработки, позволяющей получать структуры с переменной пористостью перпендикулярно поверхности оксидной пленки, благодаря изменению напряжения во время анодирования (см. рис).

Диаметры пор образцов, исследуемых в данной работе, меньше $30~ нм$. Пористая среда с таким маленьким диаметром поры становится непрерывной для электромагнитных волн в оптическом диапазоне, что позволяет описывать её эффективным (усредненным по объему) показателем преломления.
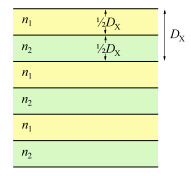
Изменение пористости оксидной пленки приводит к изменению её показателя преломления. Заметим, что показатель преломления исследуемых образцов периодически изменяется только в одном направлении: перпендикулярно поверхности пленки. Поэтому изучаемые образцы являются одномерными фотонными кристаллами.
Следует отметить, что тонкие плёнки анодного оксида алюминия c постоянным диаметром оптически прозрачны, тогда как фотонные кристаллы окрашены благодаря явлению интерференции света в их слоистой структуре.
В процессе работы вы проведете оптические исследования трех образцов фотонных кристаллов на основе анодного оксида алюминия (ААО) со структурами различной сложности.

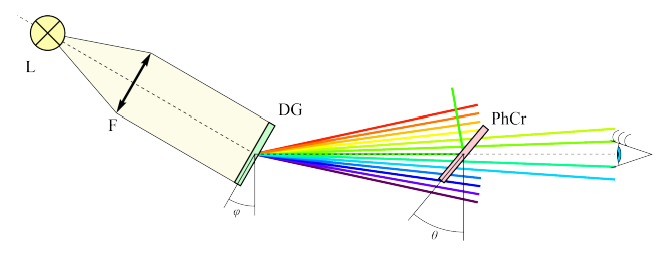
Для проведения спектральных измерений с различными длинами волн вам понадобится спектральное плечо (см. рис). Спектральное плечо состоит из лампы накаливания (L), дифракционной решетки с держателем (DG) и подвижной линзы (F) между ними. Для установки спектрального плеча поместите диск в левое отверстие в оптической скамье.

Первоначально лампа находится в центре, хотя при необходимости её положение регулируется. Убедитесь, что нить накала расположена вертикально для получения более тонкой спектральной линии после дифракционной решетки. Изменяя положение линзы, вы можете регулировать угол расходимости пучка. Для этого открутите гайку (WN), переместите держатель линзы в необходимое положение, снова затяните гайку (не затягивайте ее слишком сильно, небольшого усилия достаточно, чтобы предотвратить случайное движение линзы).
Для включения источника света вставьте вилку источника питания в розетку на столе. Подсоедините провод от источника питания к разъему лампы или лазера. Для лазеров важна полярность. Изначально она установлена правильно.
Вам выданы три лазера, промаркированные цветными лентами: красный ($\lambda = 659~ нм$), зеленый ($\lambda = 530~ нм$) и синий ($\lambda = 400~ нм$).
Лазерное излучение опасно! Не светите лазером себе в глаза ни при каких обстоятельствах! Опасайтесь отраженных лазерных лучей!
Красный и синий лазеры имеют одно крепление для питания. Для переключения с красного на синий лазер отвинтите крепление от красного лазера и привинтите его к синему (см. рис a).

Для проведения эксперимента наденьте фиксатор кнопки включения на лазер, поместите лазер в держатель и закрепите его резинкой (рис. b). Вставьте диск держателя в левое отверстие оптической скамьи. Для включения лазера поверните фиксатор кнопки включения (1).
Вам может потребоваться отрегулировать положение луча лазера. Вначале вращайте лазер вокруг своей оси до тех пор, пока луч не окажется в горизонтальной плоскости (2).
Затем поверните диск держателя, чтобы выровнять луч относительно оптической скамьи (3).
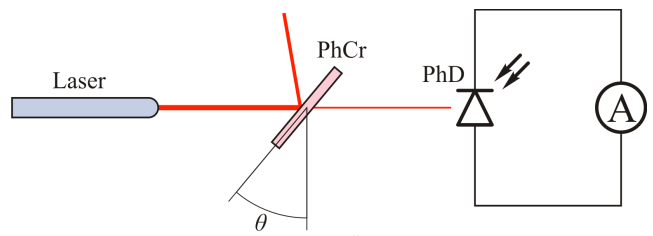
Для измерения интенсивности проходящего излучения вам понадобятся лазеры и фотодиод. Поместите ножки держателя фотодиода в соответствующие отверстия оптической скамьи (рис. a).

Фотодиод крепится к держателю с помощью магнита, его положение может регулироваться.
Для проведения измерений с фотодиодом подключите его к мультиметру в режиме постоянного тока $(\mathrm{\mu A)}$ (рис. b). Ток фотодиода пропорционален интенсивности падающего света, поэтому мы будем измерять интенсивность света в $(\mathrm{\mu A)}$.
Фотонные кристаллы очень хрупкие! Не прикасайтесь к кристаллам! Держите образцы только за рамку!
Вам выданы три образца различных фотонных кристаллов. Лицевые стороны рамок обозначены разными буквами, в соответствии с названием образца (X, Y, Z) и имеют разный цвет. При размещении образца в держателе проверьте, что луч падает на лицевую поверхность, а буква расположена в верхней части рамки. Для проведения измерений поместите диск держателя в правое отверстие оптической скамьи. Вращайте диск держателя только по часовой стрелке, чтобы отвести отраженный луч света.

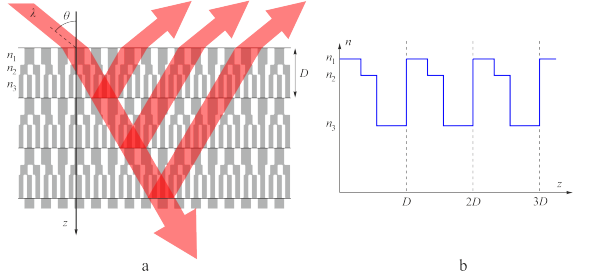
Образцы фотонных кристаллов, исследуемые в данной задаче, состоят из слоев с разными показателями преломления $n_i$. Показатель преломления периодически изменяется вдоль оси $z$ с периодом $D$ и не зависит от длины волны $\lambda$. Обозначим средний показатель преломления $n$, а изменение показателя преломления $\Delta n=n_{\mathrm{max}}-n_{\mathrm{min}}$. В кристаллах ААО $$\Delta n\ll n.$$ Рассмотрим параллельный монохроматический пучок с постоянной интенсивностью и длиной волны $\lambda$, падающий на фотонный кристалл. Угол падения равен $\theta$. Пучки, отраженные от разных слоев, интерферируют между собой. В результате интерференционная картина в отраженном свете имеет максимумы при определенных углах $\theta$, которые определяются условием: $$2D\sqrt{n^2-\sin^2\theta}=m\lambda,$$ где $m = 1, 2, ...$ целые числа, означающие порядок интерференции.
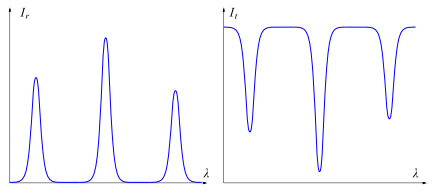
Данное выражение называется законом Брэгга-Снелла. Минимумы пропускания наблюдаются при тех же углах $\theta$. Если угол остается постоянным, а длина волны $\lambda$ изменяется, закон Брэгга-Снелла. можно использовать, как уравнение для нахождения $\lambda$. На рис. ниже представлены спектры отражения и пропускания. Каждый минимум пропускания соответствует целому числу $m$ в законе Брэгга-Снелла.
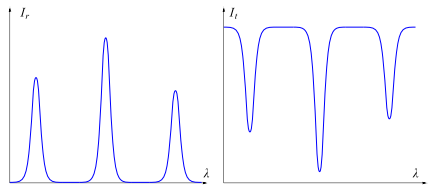
Длины волн, удовлетворяющие закону Брэгга-Снелла, будем называть длинами волн минимумов пропускания. Длины волн минимумов пропускания зависят от угла падения $\theta$. Длины волн минимумов пропускания при $\theta=0$ будем называть нормальными длинами волн минимумов пропускания для данного фотонного кристалла.
В этой задаче не требуется рассчитывать погрешность измерений.
Образец X имеет простую структуру (см. рис). Его период состоит из двух слоев с одинаковой толщиной $D_X/2$ и с показателями преломления $n_1$ и $n_2$ мало отличающимися друг от друга: $$n_1-n_2=\Delta n\ll n_X=\frac{n_1+n_2}{2}$$
1. Соберите экспериментальную установку для спектральных измерений. Поместите скамью с источником света и дифракционной решеткой для спектральных измерений (спектральное плечо) в левое отверстие оптической скамьи с транспортирами.
2. Включите лампу. Посмотрите на свет от лампочки сквозь дифракционную решетку на другом конце оптической скамьи. Вращайте спектральное плечо до тех пор, пока не увидите первый дифракционный максимум (полоску радуги).
3. Установите держатель образца в правое отверстие оптической скамьи (установите треугольную метку на ноль). Поместите образец X в держатель (свет должен падать на красную лицевую поверхность). Посмотрите на радужную полоску после дифракционной решетки через образец (спектр пропускания).
4. Если вы будете вращать по часовой стрелке образец, то вы сможете увидеть темную полоску в спектре пропускания (см. рис. ниже). Это минимум пропускания соответствующий $m=1$ в законе Брэгга-Снелла. Когда вы вращаете образец, длина волны минимума пропускания изменяется.
5. Перемещая линзу, вы можете наблюдать более широкую или узкую часть спектра. Для точных измерений расположите линзу таким образом, чтобы лампочка была расположена в фокусе.

Пористость кристалла $p$ это доля объема кристалла заполненного воздухом (в воздушных каналах). Эффективный показатель преломления может быть выражен через показатель преломления воздуха $n_a=1$ и показатель преломления оксида алюминия $n_{AAO}$: $$n_{dry}=\sqrt{pn_a^2+(1-p)n^2_{AAO}}.$$ Если каналы заполнить водой, то показатель преломления кристалла изменится: $$n_{wet}=\sqrt{pn_w^2+(1-p)n^2_{AAO}},$$ где $n_w=1.33$ показатель преломления воды.
В этом задании мы будем определять пористость $p$ фотонного кристалла, сравнивая результаты экспериментов для ”сухого” образца и образца заполненного водой. Мы будем использовать установку с лазером в качестве источника света.
Используйте выбранный лазер во всех заданиях части В.
Соберите экспериментальную установку для измерений с лазером (см. рис. ниже). Перед проведением измерений с лазерным излучением убедитесь, что интенсивность лазера постоянна. Если это не так, подождите 3—5 минут.
Не допускайте попадания лазерного пучка вам в глаза! Следите за отраженными лучами, они также не должны попадать вам в глаза. Даже короткая экспозиция может серьезно повредить ваше зрение. Не держите голову на уровне луча, когда вы проводите какие-либо эксперименты с лазерным излучением.
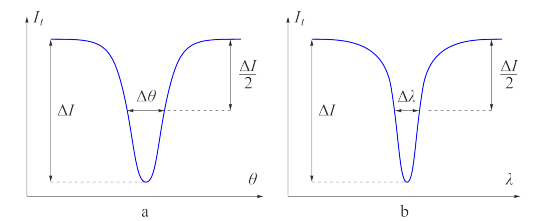
Когда свет падает перпендикулярно кристаллу $(\theta = 0)$, спектральная ширина $\Delta\lambda$ (рис. b) минимума пропускания, соответствующая $m = 1$, может быть выражена через $n$ и $\Delta n$ следующим образом: $$\frac{\Delta \lambda}{\lambda}=\frac2\pi\frac{\Delta n}{n}.$$ Для того, чтобы оценить $\Delta n_X$ для образца Х, будем предполагать, что относительная спектральная ширина минимума пропускания $\frac{\Delta \lambda}{\lambda}$ при изменении угла падения не изменяется.
Нанесите немного воды на лицевую сторону образца X. Для предотвращения испарения воды во время эксперимента, поместите покровное стекло на образец. На обратной стороне образца имеется слой твердого оксида толщиной $15~нм$, препятствующий выливанию воды.
Будьте осторожны! Образцы очень хрупкие. Их ширина составляет четверть диаметра волоса. Берите образцы только за рамку. Покровное стекло также очень хрупкое! Держите его только с помощью пинцета.
Структура образца Y более сложная чем у образца Х. Образец Y имеет четыре минимума пропускания в видимом спектральном диапазоне $(400-800~ нм)$, соответствующие четырем последовательным целым числам $m$ в законе Брэгга-Снелла. Показатели преломления образцов Х и Y одинаковые $n_Y=n_X$.
Теперь проведите измерения с лазером для образца Y (см. Задание B). Измерения с лазером позволяют определить нормальные длины волн минимумов пропускания с большей точностью. Кроме того, вы сможете определить значения коэффициентов пропускания, которые вам понадобятся в части E.

c.8
0.60
Определите значения коэффициентов пропускания $t$ для четырех минимумов пропускания образца Y (см. рис. выше).
Эти значения будут использованы в задании Е для определения структуры образца Y. Вы можете построить график, если вам это необходимо, хотя это и не является обязательным требованием.
Закон Брэгга - Снелла определяет углы и длины волн, при которых может наблюдаться минимум пропускания. Значение коэффициента пропускания $t$ зависит от внутренней структуры периода образца. Он может иметь такую структуру, что некоторые минимумы, которые предсказывает закон Брэгга - Снелла, имеют значение коэффициента пропускания, равное $1(t=1)$ и поэтому не наблюдаются. Будем называть такие минимумы пропускания пропавшими минимумами пропускания. Те минимумы, которые не пропали, мы будем называть видимыми.
Считается, что минимум пропускания пропал, если он не может быть замечен в спектральных измерениях или измерениях с лазером при тех значениях углов и длин волн, которые предсказаны законом Брэгга-Снелла. Образец Y не имеет пропавших минимумов пропускания. Наоборот, образец Z имеет 2 пропавших минимума в видимом спектре. Это означает, что не все видимые минимумы пропускания соответствуют последовательным значениям $m$.
Средние показатели преломления образцов Х и Z совпадают: $n_Z=n_X$.
Закон Брэгга - Снелла определяет углы и длины волн, при которых могут наблюдаться максимумы отражения или минимумы пропускания (см. рис). Величина пропускания определяется внутренней структурой периода.
В этом задании обсуждается упрощенная теория вычисления коэффициента отражения. Рассматривается случай нормального падения волны $(\theta=0)$. В этом случае закон Брэгга-Снелла имеет вид: $$2Dn=m\lambda$$ где $D$ — период кристалла.
В этой модели мы предполагаем, что свет отражается только от той границы, где он переходит из области с большим показателем преломления в область с меньшим. Отражающие границы, рассматриваемые в модели, отмечены на рис. ниже стрелками.
Образцы X, Y и Z состоят из слоев, которые могут иметь только одно из двух заданных значений показателей преломления и только одну фиксированную толщину. Поэтому мы ограничимся рассмотрением только этого частного случая.
Обозначим $d_l$ толщину двух слоев, $D$ период кристалла, $\delta_j$ расстояние между началом периода и отражающей границей с номером $j$.

Например, структура представленная на рисунке имеет период $D=3.5d_l$, расстояние между началом периода и отражающими границами $\delta_1=0, \delta_2=d_l,\delta_3=2.5d_l$.
Для луча, который отразился от границы $j$, набег фазы определяется выражением $$
\varphi_{j_m}=2 \pi \frac{2 \delta_j n}{\lambda}=2 \pi m \frac{\delta_j}{D}
$$ Рассматривая интерференцию между лучами, отраженными от границ одного периода, мы находим, что интенсивность отраженного излучения для максимума с номером $m$ из закона Брэгга-Снелла равна: $$
I_{{refl}, m} \sim\left|\sum_j \exp \left(i \varphi_{j_m}\right)\right|^2
$$ где $i$ — мнимая единица.
Модель, рассмотренная выше, не позволяет получить точное значение величины максимумов интенсивности отраженного света, но она сохраняет знак неравенства между ними, т.е. вы можете сравнить величины максимумов и сказать какой из них больше. Если интенсивность отраженного излучения большая, то величина коэффициента пропускания $t$ является маленькой. Если значение максимума отраженного излучения достаточно низкое, то мы считаем, что это соответствует случаю пропавшего минимума.
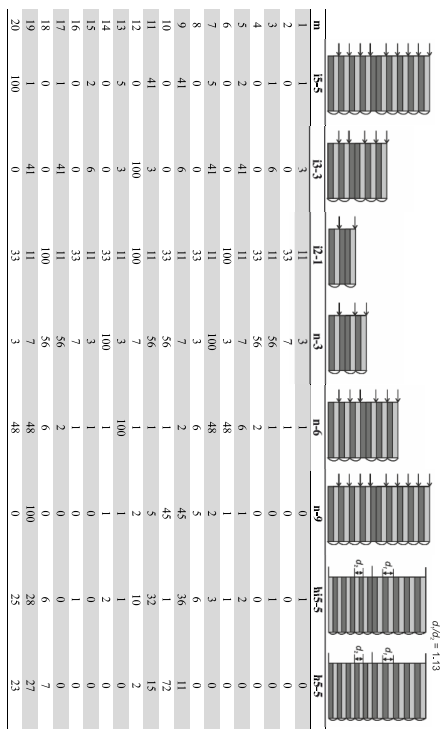
В приложении есть таблица со значениями $I_m/I_0$, вычисленными согласно уравнению $$
I_{{refl}, m} \sim\left|\sum_j \exp \left(i \varphi_{j_m}\right)\right|^2
$$ для целых $m$ от $1$ до $20$. Интенсивность $I_0$ рассчитывается согласно уравнению для значения $m = 0$. В этом случае все отраженные лучи интерферируют без фазового сдвига, что дает максимально возможную интенсивность. Значения $I_m/I_0$ представлены в $\%$.
Среди представленных структур есть структуры образцов Y и Z.
Возможные варианты структур образцов Y и Z. Названия структур приведены под рисунками. Числовые значения $I_m/I_0$ представлены в таблице в $\%$.