Введение

С развитием современных технологий (в т.ч. беспилотных автомобилей) становятся востребованы LiDAR (англ. Light Detection and Ranging) — приборы для измерения расстояния до объектов в режиме реального времени. Прибор посылает лазерные импульсы к объекту и измеряет время, через которое рассеянный сигнал будет принят фотодетектором. Одним из перспективных видов таких фотодетекторов, способных быстро детектировать короткие импульсы ($<1~\text{нс}$) в широком динамическом диапазоне, являются ТФУ (твердотельные фотоумножители).

ТФУ образован матрицей параллельно соединенных ячеек. Каждая ячейка приближённо представляет из себя $p\text{-}n$ переход на кремнии и нанесенный на него диэлектрический слой с утечкой (слой гашения). Кремний является полупроводником, и при нормальных условиях электроны в нем почти не проводят электрический ток. Однако, при попадании света на ячейку, электрон в полупроводнике может стать проводящим. Разгоняясь в достаточно сильном электрическом поле, этот электрон «выбивает» другие электроны в проводящее состояние, новые электроны также разгоняются, и так далее — этот процесс называется лавинной ударной ионизацией. На границе слоя гашения при этом накапливается заряд, который экранирует поле в области умножения, и лавина затухает.

Изготовление опытного образца ТФУ — сложный и дорогостоящий технологический процесс, а непосредственное численное моделирование электрофизики многоячеистого прибора затруднено из-за ограничений по вычислительной мощности, поэтому полезно заранее оценивать характеристики сконструированного прибора. Для упрощения расчетов разработана модель эквивалентной электрической схемы ТФУ, состоящая из линейных компонентов (резисторы, емкости, индуктивности) — приближенно описывающая компоненты реального детектора.

Рассмотрим эквивалентную электрическую схему ТФУ, подключенную к источнику питания и измерительному устройству.

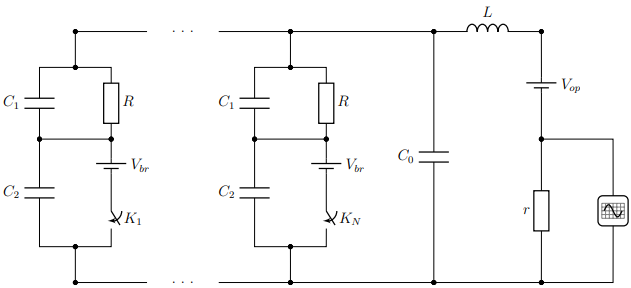
Опишем компоненты эквивалентной схемы и допускаемые приближения:

•  В левой части схемы расположена матрица ТФУ, состоящая из $N=5\cdot{10^4}$ параллельно соединенных ячеек и паразитной (межъячеечной) емкости $C_0$. Каждая ячейка  упрощенно представляет из себя последовательное соединение $p\text{-}n$ перехода и слоя гашения.
• $p\text{-}n$ переход в диапазоне прикладываемых к нему напряжений в обратном смещении $\bigl[V_{br}{,}V_{op}\bigr]$ можно аппроксимировать постоянной емкостью $C_2$.
• Лавинный процесс приводит к тому, что напряжение на $p\text{-}n$ переходе мгновенно падает до напряжения пробоя $V_{br}$. Время этого процесса много меньше характерных времен всех остальных процессов в цепи.  С точки зрения нашей цепи лавинный процесс  при попадании света на ячейку с номером $i$ представляет собой кратковременное замыкание ключа $K_i$ и мгновенное падение напряжения на $p\text{-}n$ переходе до $V_{br}=63~\text{В}$. Все остальное время ключи $K_i$ разомкнуты. 
• Слой гашения обладает постоянной емкостью $C_1$ и сопротивлением утечки $R=100~\text{МОм}$.
• Паразитная индуктивность ножек детектора и соединительных элементов – $L=1~\text{нГн}$. 
• ТФУ последовательно соединен с источником постоянного рабочего напряжения $V_{op}=65~\text{В}$. 
• Измерительное устройство эквивалентно нагрузке сопротивлением $r=50~\text{Ом}$ и идеальному вольтметру (осциллографу). 

Для удобства вычислений введем дополнительные обозначения: 

• $C_{cell}=\cfrac{C_1C_2}{C_1+C_2}$ — емкость одной ячейки 
• $C_{det}=NC_{cell}+C_0=20~\text{пФ}$ — емкость детектора 
• $k=C_1/C_2=5$ — отношение емкостей слоя гашения и $p-n$ перехода 
• $p=C_0/C_{det}=0{.}1$ — отношение паразитной емкости к емкости детектора 
• $V_{ov}=V_{op}-V_{br}=2~\text{В}$ — величина перенапряжения на приборе.

Часть A. Лавинный процесс (2.5 балла)

Пусть схема находится в установившемся режиме, то есть на нее в течении очень большого времени не попадало световых импульсов и ключи $K$ были разомкнутыми.

A1  ^0.40

Для установившегося режима найдите:

• напряжение $V_r$ на нагрузке $r$;
• напряжение $V_0$ на каждой ячейке и паразитной емкости $C_0$;
• напряжения $V_1$ на слоях гашения каждой ячейки.

В условиях установившегося режима свет попадает одновременно на $n$ ячеек. Рассмотрим состояние схемы через настолько малое время после попадания света, что зарядом, протекшим через индуктивность можно пренебречь. Также можно пренебречь и протеканием заряда через сопротивления утечки $R$. Пусть $\Delta{V}$ — изменение напряжения на конденсаторе $C_0$ и на ячейках по завершении лавинного процесса. Полярность изменения напряжения примите той же, что и полярность напряжения в установившемся режиме.

A2  ^0.80

Найдите: 

• изменение заряда $\Delta{q}_0$ конденсатора $C_0$. Ответ выразите через $C_0$ и $\Delta{V}$;
• изменения зарядов $\Delta{q}_{1a}$ и $\Delta{q}_{2a}$ конденсаторов $C_1$ и $C_2$ соответственно каждой из активных ячеек. Ответы выразите через $C_1$, $C_2$, $V_{ov}$ и $\Delta{V}$;
• изменения зарядов $\Delta{q}_{1p}$ и $\Delta{q}_{2p}$ конденсаторов $C_1$ и $C_2$ соответственно каждой из пассивных ячеек. Ответы выразите через $C_{cell}$ и $\Delta{V}$.

A3  ^0.70 Найдите изменение напряжения $\Delta{V}$ на ячейках и конденсаторе $C_0$ по завершении лавинного процесса . Ответ выразите в общем виде через $V_{ov}$, $n$, $N$, $C_1$, $C_2$, $C_0$.

Из-за тепловых флуктуаций на нагрузке может возникать шумовой сигнал, амплитуду которого можно оценить по формуле $V_{noise}=\sqrt{4k_BTrf}$, где $k_B=1{.}38\cdot{10^{-23}}~\text{Дж}/\text{К}$ — постоянная Больцмана, $T$ — температура нагрузки (в Кельвинах), $r$ — сопротивление нагрузки, $f$ — частотная полоса пропускания измерительного прибора (осциллографа).

A4  ^0.60 Оцените амплитуду теплового шума на нагрузке $r=50~\text{Ом}$ при комнатной температуре, если полоса пропускания осциллографа составляет $1~\text{ГГц}=10^9~\text{Гц}$. Используя данные из условия задачи и полученную вами формулу из A3 найдите численное значение $\Delta{V}$ при попадании света на одну ячейку.  Cделайте вывод о том, можно ли различить сигнал от одной ячейки на фоне теплового шума сопротивления нагрузки.

Часть B. Коэффициент умножения (0.8 балла)

Одной из важных характеристик ТФУ является коэффициент умножения $M$: $$M=\cfrac{Q}{e} ,$$ где $Q$ — заряд, протекший через нагрузку $r$ после попадания света на одну из ячеек за очень большое время, за которое цепь успевает полностью вернуться в установившийся режим. Изначально цепь также находилась в условиях установившегося режима. Здесь $e=1{.}6\cdot{10^{-19}}~\text{Кл}$ — элементарный заряд.

B1  ^0.80 Найдите коэффициент умножения $M$ для ТФУ с параметрами из условия задачи. Выразите ответ через $N$, $C_1$, $C_2$, $C_0$, $e$, $V_{ov}$ и приведите численное значение.

Часть C. Импульс фотосвета (1.2 балла)

C1  ^0.40 Рассмотрим импульс, регистрируемый осциллографом после попадания света на одну ячейку. Будем считать, что длительность импульса достаточно мала, чтобы пренебречь током, протекающим через сопротивление утечки $R$, но достаточно большое, чтобы лавинный процесс завершился, и все ключи $K_i$ разомкнуты. В этом приближении можно заменить цепь на эквивалентную последовательную $RLC$ цепь. Укажите ее параметры.

C2  ^0.30 Оцените добротность полученной $RLC$ цепи. Возникнут ли в этой цепи колебания?

C3  ^0.30 Качественно изобразите график зависимости напряжения на нагрузке от времени после попадания света на одну из ячеек. Первоначально схема находилась в установившемся режиме. Характерные значения указывать не обязательно.

C4  ^0.20 Сравните максимальное по модулю значение напряжения на нагрузке $|V_{max}|$ после попадания света на одну из ячеек и найденную ранее величину $|\Delta{V}|$ . Какая из этих величин больше? Обведите в листе ответов правильное соотношение.

Часть D. Восстановление ячеек (1.5 балла)

D1  ^1.00 Найдите приближенную зависимость напряжения на слое гашения ячейки от времени после попадания света на нее (в первоначальных условиях установившегося режима). Воспользуйтесь тем, что в условиях данной задачи $\Delta{V}\ll{V_{ov}}$, $R\gg{r}$. Считайте, что прошло достаточно много времени, и напряжение на внешней нагрузке практически равно нулю. Выразите ответ через $V_{ov}$, $R$, $C_1$, $C_2$, $t$.

D2  ^0.50 Найдите  изменение напряжения $\Delta{V}$ на  конденсаторе $C_0$ при попадании света на одну ($n=1$) из невосстановленных ячеек, напряжение на слое гашения которой равнялось $V_1<V_{ov}$. Считайте, что до попадания света на эту ячейку напряжение на всех ячейках и паразитной емкости соответствовало установившемуся режиму.  Выразите $\Delta{V}$ через $V_{ov}$, $V_1$, $N$, $C_1$, $C_2$, $C_0$.

Часть E. Шум фотодетектора (2.0 балла)

Основная причина, затрудняющая достоверную регистрацию полезного сигнала в системах активного лазерного сканирования - это шумовой сигнал от фоновой засветки (рассеянный от объекта солнечный свет, свет фар встречных автомобилей и т. д.). В этом разделе задачи проанализируем характеристики сигнала под воздействием равномерной фоновой засветки детектора.

Пусть фоновая засветка имеет такую интенсивность, что вероятность срабатывания каждой ячейки за время $dt$ равна $dt/ T$ и не зависит от времени до предыдущего срабатывания. $T$ — характерный промежуток времени между срабатываниями ячейки. Примем за 1 амплитуду импульса фотоответа (то есть максимальное значение сигнала на осциллографе) при попадании света на полностью восстановленную ячейку. Если ячейка восстановилась не полностью, амплитуда импульса фотоответа зависит от времени $t$, прошедшего с момента предыдущего срабатывания ячейки, как ($\tau$ — характерное время восстановления ячейки)
$$ V=1-e^{-t/\tau}.$$

E1  ^0.30 Пусть $p(t)$ — вероятность того, что в течение времени $t$ ячейка не сработала ни разу. Найдите $p(t + dt)$, выразите ответ через $p(t)$, $dt$, $T$. Считайте, что $dt \ll T$.

E2  ^0.20 Найдите вероятность того, ячейка не сработает ни разу в течение времени $t$. Ответ выразите через $t$, $T$.

E3  ^0.20 Пусть ячейка сработала в момент времени $t = 0$. Найдите вероятность того, что в следующий раз она сработает в интервал времен от $t$ до $t + dt$.

E4  ^0.40 Найдите среднюю амплитуду импульсов фотоответа $\mu$. Считайте, что разные ячейки создают импульсы независимо друг от друга.

E5  ^0.60 Найдите среднеквадратичное отклонение амплитуды импульсов фотоответа $\sigma$. Ответ выразите через $\tau$ , $T$.

Указание: среднеквадратичное отклонение можно вычислить по формуле $\sigma=\sqrt{\mu(V^2)-\mu^2(V)}$, где $\mu(V^2)$ — среднее значение квадрата амплитуды, $\mu^2(V)$ — квадрат среднего значения амплитуды.

Введём понятие соотношения сигнал-шум ($SNR$, англ. signal-to-noise ratio), как отношение средней величины сигнала к его среднеквадричному отклонению:
$$SNR=\cfrac{\mu}{\sigma}
$$
По величине $SNR$ можно косвенно судить о динамическом диапазоне и чувствительности детектора: чем больше $SNR$, тем лучше эти характеристики.

E6  ^0.30

Найдите $SNR$ амплитуд импульсов фотоответа под воздействием равномерной фоновой засветки в случаях:

• $\tau=0$;
• $\tau\gg{T}$;
• $\tau=T$.