A1  ^0.40

Для установившегося режима найдите:

• напряжение $V_r$ на нагрузке $r$;
• напряжение $V_0$ на каждой ячейке и паразитной емкости $C_0$;
• напряжения $V_1$ на слоях гашения каждой ячейки.

В установившемся режиме ток через $r$ не течёт, поэтому $V_r = 0$. Напряжение на ячейках совпадает с напряжением источника, то есть $V_0 = V_{op}$. Конденсатор $C_1$ параллелен резистору, поэтому он разряжен: $V_1 = 0$.

A2  ^0.80

Найдите: 

• изменение заряда $\Delta{q}_0$ конденсатора $C_0$. Ответ выразите через $C_0$ и $\Delta{V}$;
• изменения зарядов $\Delta{q}_{1a}$ и $\Delta{q}_{2a}$ конденсаторов $C_1$ и $C_2$ соответственно каждой из активных ячеек. Ответы выразите через $C_1$, $C_2$, $V_{ov}$ и $\Delta{V}$;
• изменения зарядов $\Delta{q}_{1p}$ и $\Delta{q}_{2p}$ конденсаторов $C_1$ и $C_2$ соответственно каждой из пассивных ячеек. Ответы выразите через $C_{cell}$ и $\Delta{V}$.

По определению ёмкости: $\Delta q_0 = C_0\Delta V$. Аналогично изменение заряда на конденсаторах в активных ячейках: $\Delta q_{1a} = C_1(V_{ov} + \Delta V)$ и $\Delta q_{2a} = -C_2 V_{ov}$, а на пассивных ячейках: $\Delta q_{1p} = \Delta q_{2p} = C_{cell} \Delta V$.

A3  ^0.70 Найдите изменение напряжения $\Delta{V}$ на ячейках и конденсаторе $C_0$ по завершении лавинного процесса . Ответ выразите в общем виде через $V_{ov}$, $n$, $N$, $C_1$, $C_2$, $C_0$.

Запишем закон сохранения заряда для положительных обкладок $C_0$ и $C_1$. $$n\Delta q_{1a} + \Delta q_0 + (N-n)\Delta q_{1p} = 0$$
$$n C_1(V_{ov} + \Delta V) + C_0\Delta V + (N-n)C_{cell} \Delta V = 0$$
$$\Delta V (nC_1 + C_0 + (N-n)C_{cell}) = - nC_1 V_{ov}$$
$$\Delta V = -\cfrac{ nC_1 V_{ov}}{nC_1 + C_0 + (N-n)\cfrac{C_1 C_2}{C_1 + C_2}}$$

A4  ^0.60 Оцените амплитуду теплового шума на нагрузке $r=50~\text{Ом}$ при комнатной температуре, если полоса пропускания осциллографа составляет $1~\text{ГГц}=10^9~\text{Гц}$. Используя данные из условия задачи и полученную вами формулу из A3 найдите численное значение $\Delta{V}$ при попадании света на одну ячейку.  Cделайте вывод о том, можно ли различить сигнал от одной ячейки на фоне теплового шума сопротивления нагрузки.

Подставим $T = 300 \text{К}$ и получим: $V_{noise} = 2.88\cdot10^{-5} \text{В}$.
Выразим изменение напряжения через данные в условии величины:
$$\Delta V = -\cfrac{(k+1)(1-p)\cfrac{n}{N}V_{ov}}{1 + \cfrac{kn}{N}(1-p)}$$
Подставим $n = 1$ и получим:
$$\Delta V = -2.16\cdot10^{-4} \text{В}$$
Заметим, что $\Delta V$ по модулю заметно больше $V_{noise}$, поэтому различить сигнал можно.

B1  ^0.80 Найдите коэффициент умножения $M$ для ТФУ с параметрами из условия задачи. Выразите ответ через $N$, $C_1$, $C_2$, $C_0$, $e$, $V_{ov}$ и приведите численное значение.

$Q$ можно определить через изменение зарядов на отрицательных обкладках $C_0$ и $C_2$.
$$Q = - C_0 \Delta V - (N - 1)C_{cell} \Delta V + C_2 V_{ov}$$
$$M =\left( (C_0 + (N-1)C_{cell})\cfrac{ C_1 V_{ov}}{C_1 + C_0 + (N-1)C_{cell}} + C_2 V_{ov}\right)\cdot\cfrac{1}{e}$$
$$M = 32.4\cdot10^3$$

C1  ^0.40 Рассмотрим импульс, регистрируемый осциллографом после попадания света на одну ячейку. Будем считать, что длительность импульса достаточно мала, чтобы пренебречь током, протекающим через сопротивление утечки $R$, но достаточно большое, чтобы лавинный процесс завершился, и все ключи $K_i$ разомкнуты. В этом приближении можно заменить цепь на эквивалентную последовательную $RLC$ цепь. Укажите ее параметры.

C2  ^0.30 Оцените добротность полученной $RLC$ цепи. Возникнут ли в этой цепи колебания?

C3  ^0.30 Качественно изобразите график зависимости напряжения на нагрузке от времени после попадания света на одну из ячеек. Первоначально схема находилась в установившемся режиме. Характерные значения указывать не обязательно.

C4  ^0.20 Сравните максимальное по модулю значение напряжения на нагрузке $|V_{max}|$ после попадания света на одну из ячеек и найденную ранее величину $|\Delta{V}|$ . Какая из этих величин больше? Обведите в листе ответов правильное соотношение.

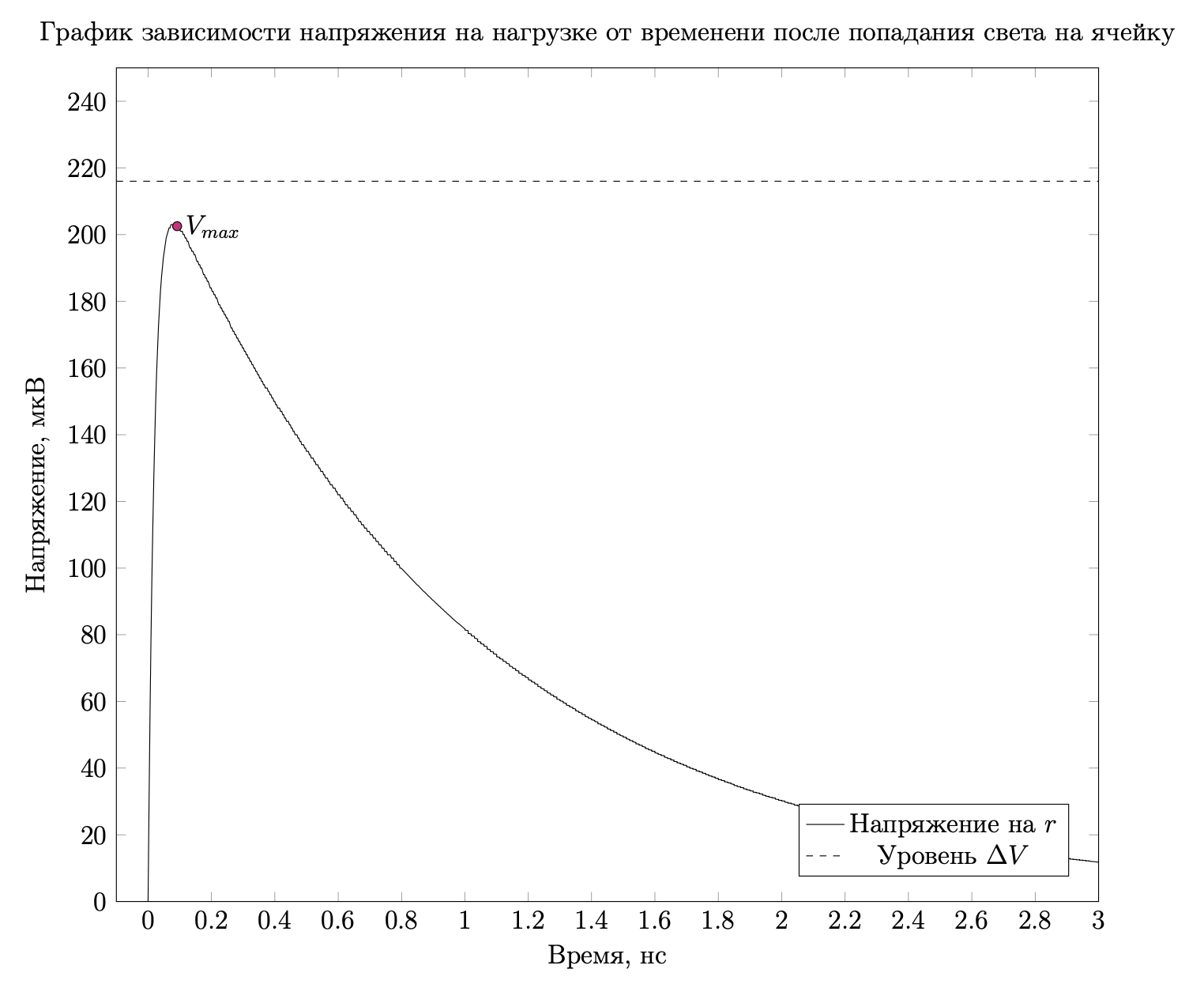
Напряжение на резисторе всегда будет меньше начального напряжения конденсатора.

D1  ^1.00 Найдите приближенную зависимость напряжения на слое гашения ячейки от времени после попадания света на нее (в первоначальных условиях установившегося режима). Воспользуйтесь тем, что в условиях данной задачи $\Delta{V}\ll{V_{ov}}$, $R\gg{r}$. Считайте, что прошло достаточно много времени, и напряжение на внешней нагрузке практически равно нулю. Выразите ответ через $V_{ov}$, $R$, $C_1$, $C_2$, $t$.

В силу соотношений данных в условии напряжением на $r$ и $L$ можно пренебречь. То есть для процесса восстановления ячейка эквивалента RC-цепи.

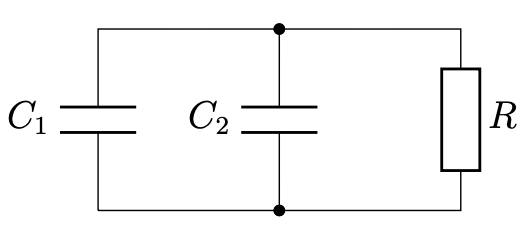
Изначально напряжение на $C_1$ равно $V_{ov}$. Тогда зависимость от времени:
$$V_1 = V_{ov}\cdot e^{-\cfrac{t}{R(C_1 + C_2)}}$$

D2  ^0.50 Найдите  изменение напряжения $\Delta{V}$ на  конденсаторе $C_0$ при попадании света на одну ($n=1$) из невосстановленных ячеек, напряжение на слое гашения которой равнялось $V_1<V_{ov}$. Считайте, что до попадания света на эту ячейку напряжение на всех ячейках и паразитной емкости соответствовало установившемуся режиму.  Выразите $\Delta{V}$ через $V_{ov}$, $V_1$, $N$, $C_1$, $C_2$, $C_0$.

Ответ можно получить аналогично части А, но теперь изменение напряжения на $C_2$ будет $V_{ov} - V_1$ вместо просто $V_{ov}$.

E1  ^0.30 Пусть $p(t)$ — вероятность того, что в течение времени $t$ ячейка не сработала ни разу. Найдите $p(t + dt)$, выразите ответ через $p(t)$, $dt$, $T$. Считайте, что $dt \ll T$.

Вероятность того, что ячейка не сработает за время $dt$ равна $1 - \cfrac{dt}{T}$, поэтому:
$$p(t+dt) = p(t) \cdot\left(1 - \cfrac{dt}{T}\right)$$

E2  ^0.20 Найдите вероятность того, ячейка не сработает ни разу в течение времени $t$. Ответ выразите через $t$, $T$.

Воспользуемся результатом прошлого пункта.
$$dp = -p\cdot\cfrac{dt}{T}$$
$$\cfrac{dp}{p} = -\cfrac{dt}{T}$$
Используя $p(0) = 1$, получим:

E3  ^0.20 Пусть ячейка сработала в момент времени $t = 0$. Найдите вероятность того, что в следующий раз она сработает в интервал времен от $t$ до $t + dt$.

Искомое выражение - произведение вероятности того, что ячейка не сработает за время $t$, и вероятности срабатывания за $dt$.

E4  ^0.40 Найдите среднюю амплитуду импульсов фотоответа $\mu$. Считайте, что разные ячейки создают импульсы независимо друг от друга.

Из определения среднего:
$$\mu = \int\limits_0^{+\infty} V(t)\cdot p(t) \cdot \cfrac{dt}{T} = \int\limits_0^{+\infty} \left(1 - e^{-\cfrac{t}{\tau}}\right)\cdot e^{-\cfrac{t}{T}} \cdot \cfrac{dt}{T} = \int\limits_0^1 \left(1 - x^{\cfrac{T}{\tau}}\right)dx$$
Где $x = e^{-\cfrac{t}{T}}$.
$$\mu = 1 - \cfrac{1}{\cfrac{T}{\tau} +1} = \cfrac{T}{T + \tau}$$

E5  ^0.60 Найдите среднеквадратичное отклонение амплитуды импульсов фотоответа $\sigma$. Ответ выразите через $\tau$ , $T$.

Указание: среднеквадратичное отклонение можно вычислить по формуле $\sigma=\sqrt{\mu(V^2)-\mu^2(V)}$, где $\mu(V^2)$ — среднее значение квадрата амплитуды, $\mu^2(V)$ — квадрат среднего значения амплитуды.

$\mu(V)$ нашли в прошлом пункте, аналогично найдём $\mu(V^2)$:
$$\mu(V^2) = \int\limits_0^1\left(1 - x^{\cfrac{T}{\tau}}\right)^2dx = 1 - \cfrac{2}{\cfrac{T}{\tau}+1} + \cfrac{1}{\cfrac{2T}{\tau}+1}$$
$$\mu(V^2) - \mu(V)^2 = \cfrac{1}{\cfrac{2T}{\tau}+1} - \cfrac{1}{\left(\cfrac{T}{\tau}+1\right)^2} = \cfrac{\cfrac{T^2}{\tau^2}}{\left(\cfrac{T}{\tau}+1\right)^2\left(\cfrac{2T}{\tau}+1\right)} = \left(\cfrac{T}{T+\tau}\right)^2\cdot\cfrac{\tau}{2T+\tau}$$
$$\sigma = \cfrac{T}{T+\tau}\cdot\sqrt{\cfrac{\tau}{2T + \tau}}$$

E6  ^0.30

Найдите $SNR$ амплитуд импульсов фотоответа под воздействием равномерной фоновой засветки в случаях:

• $\tau=0$;
• $\tau\gg{T}$;
• $\tau=T$.

$$SNR = \sqrt{\cfrac{2T + \tau}{\tau}}$$