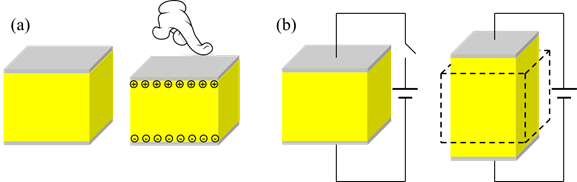
Пьезоэлектрическим эффектом называется процесс появления электрических зарядов в твердых телах вследствие приложенного механического напряжения (рис. 1(a)). Он является обратимым. Это означает, что материалы, обладающие пьезоэлектрическим эффектом, также обладают обратным пьезоэлектрическим эффектом, т.е. вследствие приложенного электрического поля появляются внутренние механические напряжения (рис. 1(b)).

Пьезоэлектрические материалы находят широкое применение в различных областях от промышленности до бытового применения: генерация и регистрация звука, генерация высокого напряжения, микровесы, сверхточная фокусировка оптических систем, зажигалки для сигарет, стартеры и кварцевые наручные часы.

Помимо упомянутого выше, пьезоэлектрические материалы также активно применяются в научных исследованиях. Ввиду того, что очень сильные электрические поля соответствуют совсем небольшим изменениям размеров пьезоэлектрических материалов, эти материалы стали наиболее важным средством позиционирования объектов с предельной точностью. На их основе созданы наиболее широко используемые приборы для изучения поверхностных явлений, такие, как сканирующий туннельный микроскоп (СТМ) и его разновидности. Нобелевская премия по физике 1986 года была присуждена Герду Биннингу и Генриху Рореру (Gerd Binnig и Heinrich Rohrer) за создание СТМ.

Другим достоинством пьезоэлектрических материалов является то, что они могут осуществлять взаимную трансформацию сигналов различного типа, таких, как механические, электрические и оптические. С помощью сверхнизких температур и современной электроники исследователи могут охладить механические моды до основного состояния и наблюдать квантование движения. Эксперимент по созданию такой квантовой машины, механического резонатора из нитрида алюминия, обладающего пьезоэлектрическими свойствами, был назван “Экспериментом 2010 года”.

Известно много пьезоэлектрических материалов, как естественных, так и искусственных. К естественным материалам относятся кварц, кость и шелк. К искусственным материалам относятся керамики, полупроводники и полимеры. Пластинка из свинца, циркония и титана (Pb[ZrxTi1−x]O3), которую мы будем называть пьезопластинкой, является в настоящее время наиболее широко используемой пьезоэлектрической керамикой, которая проявляет сильные пьезоэлектрические свойства.

В данном эксперименте вы будете изучать свойства пьезопластинки и применения пьезоэффекта. Для конкретной пьезопластинки вы измерите ее пьезоэлектрический коэффициент с помощью резонансного метода и оцените ее температуру Кюри с применением линейной экстраполяции. Вы сделаете из пьезопластинки передатчик для генерации механических колебаний и звуковых волн в среде; вы сделаете из пьезопластинки датчик для регистрации силы звуковых волн. С помощью самодельных передатчика и датчика звука вы измерите скорости продольных и поперечных звуковых волн в алюминиевом бруске. Наконец, вы используете звуковые волны для резонансного детектирования искусственного дефекта в другом алюминиевом бруске.
 

Общие меры предосторожности

1. Перед тем, как отсоединить оборудование от сети, выключите его. Иначе Вы можете повредить оборудование.
2. Не включайте водяной термостат, если нагреватель не покрыт водой.
3. Старайтесь не расплескать воду на электронные приборы, сетевые розетки и удлинители.
4. Будьте осторожны с горячей водой.
5. Опасайтесь поражения электрическим током.

Не пейте предоставленную для эксперимента воду и не используйте не по назначению ничего из того, что Вам предоставлено для эксперимента.

Инструкции по работе с генератором сигналов

1. Для включения генератора подсоедините к гнезду на его задней панели кабель с USB разъемом и адаптером переменного тока и нажмите клавишу выключателя на передней панели.
2. На дисплее отображаются частота и тип волны (синус, прямоугольник или треугольник). Вам рекомендуется в эксперименте использовать синусоидальные волны.
3. Используйте кнопку “AMPL” для регулировки амплитуды сигнала. Используйте кнопку “ADJ” для изменения частоты сигнала. Используйте клавиши “◄” или “►”для перемещения курсора.
4. Будьте аккуратны при работе с кнопкой “OFFS”. С помощью этой кнопки Вы изменяете постоянную составляющую сигнала (смещение). Большая постоянная составляющая может вызвать искажение сигнала (на рисунке (а)). Вам рекомендуется прокалибровать постоянную составляющую перед использованием генератора сигналов: с помощью ЦММ измеряйте постоянное напряжение на выходе генератора и вращайте кнопку “OFFS” до тех пор, пока постоянное напряжение не станет равным нулю.
5. Вам также рекомендуется не устанавливать кнопку “AMPL” на максимум, чтобы избежать искажения сигнала (на рисунке (b)). Вы можете для эксперимента сделать величину сигнала на выходе равной 3,0 В: используйте ЦММ для измерения переменного напряжения на выходе при частоте, например, 1 кГц, вращайте кнопку “AMPL”, пока переменное напряжение не достигнет величины около 3,0 В.
6. Если Вы нажали кнопку по ошибке и не знаете, как вернуться назад, выключите и включите генератор, и последние настройки восстановятся.

Инструкции по работе с цифровым мультиметром

1. Гнезда “VΩ” и “COM” используются для измерения напряжения, сопротивления и ёмкости.
2. Гнезда “mA” и “COM” используются для измерения силы тока.
3. Используйте вращающийся переключатель для выбора необходимой функции и диапазона измерений.
4. Символом  обозначен режим измерения ёмкости.
5. Для перехода между режимами переменного и постоянного тока используйте желтую кнопку.
6. ЦММ переходит в спящий режим и очищает дисплей в случае, если он не используется более 20 минут. Поверните вращающийся переключатель в положение OFF и обратно, чтобы «разбудить» ЦММ. Для дезактивации спящего режима удерживайте желтую кнопку при включении ЦММ.
7. Для калибровки выходного напряжения генератора сигналов с помощью ЦММ установите частоту сигнала, равную 1 кГц или ниже.

Инструкции по работе с водяным термостатом

1. Категорически запрещено включать термостат, если нагревательный элемент не покрыт водой.
2. В процессе работы термостата его поверхность может стать горячей.
3. Недопустимо попадание воды на электронные приборы, сетевые розетки и удлинители.
4. Заполните термостат примерно наполовину водой из бутылки. Подсоедините кабель питания и включите термостат.
5. Для установки требуемой температуры нажмите кнопку “Set”, и индикатор “Set” засветится. Используйте кнопки Ù и Ú для увеличения (уменьшения) заданной температуры, которая указывается на дисплее. Нажмите снова кнопку “Set” для выхода из режима установки, индикатор “Set” погаснет, и вода в термостате автоматически начнет нагреваться. Если индикатор “Set” не горит, то на дисплее показываются фактические значения температуры.
6. При нагреве светится индикатор “Heat”. После достижения заданной температуры загорится индикатор “Keep” и нагрев прекратится

Часть A. Простейшие измерения (3.0 балла)

В этом эксперименте требуется определить размеры, массу и электрическую емкость пьезопластинки, а затем рассчитать плотность $\rho$ и относительную диэлектрическую проницаемость $\varepsilon_r$ материала, из которого она изготовлена.

Выберите одну из предоставленных вам пьезопластинок. Эксперименты частей A, B и C выполняйте только с ней.

Производите расчёт погрешностей только в тех частях, где это явно сказано.

A1  ^1.60 Измерьте штангенциркулем длину $l$, ширину $w$, и толщину $t$ выбранной пьезопластинки. С помощью предоставленных электронных весов взвесьте эту пьезопластинку. Вставив пластинку в зажим Кельвина (6) измерьте мультиметром её электроемкость $C$.
Учитывая то, что размеры пластинки неодинаковы в разных точках, проведите несколько измерений, рассчитайте средние величины и их стандартные погрешности.

Внимание: Диэлектрическая проницаемость пьезопластинки зависит от температуры (что будет рассмотрено в Части С). Поэтому подразумевается, что измерения электроемкости необходимо производить при комнатной температуре, избегая нагрева пьезопластинки руками.

A2  ^1.40 Вычислите плотность $\rho$ и диэлектрическую проницаемость $\varepsilon_r$ пьезопластинки. Используя погрешности, найденные в части A1, рассчитайте погрешности величин $\rho$ и $\varepsilon_r$ (диэлектрическая постоянная $\varepsilon_0=8.85\cdot10^{-12}~\text{Ф}/\text{м}$).

Часть B. Резонансный метод измерения пьезоэлектрического коэффициента (4.5 балла)

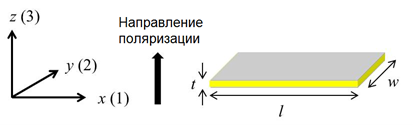
Как было описано во введении, пьезопластинка деформируется под действием электрического поля. Коэффициент пропорциональности $d$ между возникающей в пьезопластинке относительной деформацией $S$ и напряженностью электрического поля $E$ называется пьезоэлектрическим коэффициентом: $d=S/E$.

В реальности пьезопластинка анизотропна и имеет выделенное направление электрической поляризации. Для создания такой поляризации пьезопластинку нагревают до температуры, выше так называемой температуры Кюри (используется в части С), затем создают сильное постоянное электрическое поле, направленное по оси $z$ (на рисунке выше), для того, чтобы ориентировать вдоль нее дипольные моменты молекул материала пьезопластинки. После этого пьезопластинку охлаждают ниже температуры Кюри и выключают электрическое поле, тем самым пьезопластинка остается поляризованной.

Верхняя и нижняя плоские поверхности пьезопластинки покрыты тонким слоев серебра (рисунок выше) и являются электродами. Когда на электроды подаётся напряжение, между ними возникает электрическое поле $E_3$, направленное вдоль оси $z$. Введём следующие определения:

\[ d_{31} = \frac{S_1}{E_3}, \quad d_{33} = \frac{S_3}{E_3},\]

где $S_1 = \Delta l / l$ и $S_2 = \Delta t / t$ относительные деформации вдоль осей $x$ (1) и $z$ (3), соответственно. Для пьезоматериалов $d_{31}$ приблизительно равно половине $d_{33}$. При подаче напряжения $V$ на электроды пьезопластинки происходит изменение всех её размеров, но больше всего изменяется её длина $l$:

\[\Delta l = l d_{31} E_3 = \frac{l}{t} d_{31} V, \quad \Delta w = \frac{w}{t} d_{31} V, \quad \Delta t = td_{33} E_3  = d_{33} V = 2d_{33} V,\]

Где $l/t \gg w/t \gg 2$. Поэтому можно считать, что пьезопластинка изменяет свои размеры только в одном направлении, а деформациями вдоль осей $y$ и $z$ можно пренебречь. В дальнейшем $d_{31}$ обозначим просто $d$.

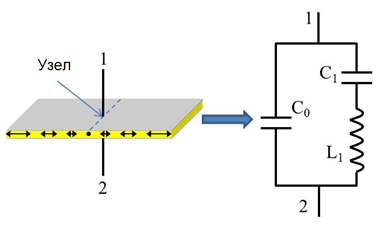
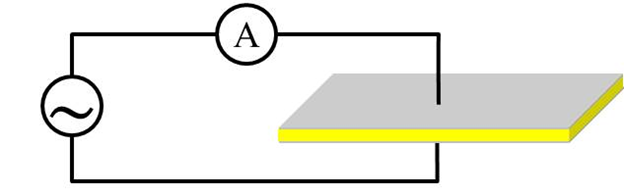
При подаче переменного электрического напряжения низкой частоты, пьезопластинка ведет себя как обыкновенный конденсатор с электроемкостью, измеренной в части A1. Однако при увеличении частоты подаваемого генератором напряжения колебания пьезопластинки сильно изменяют ее эквивалентную электрическую схему. При некоторой частоте, называемой резонансной, колебания пьезопластинки максимальны, а модуль импенданса (отношение амплитуды напряжения к амплитуде тока) минимален. Кроме этого существует и антирезонансная частота, при которой модуль импенданса максимален.

Появление резонансной частоты $f_r$ связано с изменением размеров пьезопластинки вдоль оси $x$. При частотах вблизи резонансной частоты $f_r$, пьезопластинка может быть представлена эквивалентной схемой, состоящей из двух конденсаторов ($C_0$ и $C_1$) и катушки индуктивности ($L_1$), как показано на рисунке.

B1  ^1.00 Для приведённой эквивалентной электрической схемы получите формулы для резонансной $f_r$ и антирезонансной $f_a$ частот.

Пьезоэлектрический коэффициент $d$ вычисляется по следующей формуле:
\[ d = \sqrt{\frac{\varepsilon_0 \varepsilon_r}{128 f_r^4l^2 \rho \left[\frac{1}{(2\pi f_a)^2 - (2 \pi f_r)^2} + \frac{1}{32f_r^2} \right]}}\]
Перейдем к эксперименту для определения частот $f_r$ и $f_a$, который схематически показан на рисунке ниже. Амплитуду подаваемого переменного напряжения $V$ поддерживайте постоянной, чтобы модуль импеданса определялся силой тока в цепи.

B2  ^3.50 Измерьте зависимость силы тока $I$ через пьезопластинку как функцию частоты подаваемого напряжения $f$. Постройте график зависимости $I(f)$ и определите по нему резонансную $f_r$ и антирезонансную $f_a$ частоты. Исходя из этого, вычислите пьезоэлектрический коэффициент $d$.

Указания:

1. Соедините вмести генератор сигналов, мультиметр и пьезопластинку, как показано на рис. 9. Обратите внимание на то, что пьезопластинка должна быть закреплена зажимом Кельвина посередине её длины.
2. Амплитуда напряжения на выходе генератора может слегка изменяться с частотой, даже при неизменном положении ручки “АMPL”.
3. Поскольку мультиметр не фиксирует сигналы с частотой выше $40~\text{кГц}$, проводите измерения на частотах до $40~\text{кГц}$.
4. Внимание: во время эксперимента пьезопластинка не должна ничего касаться кроме зажима. Не двигайте зажим по столу, так как это вызовет изменения в показаниях мультиметра. 
5. Внимание: как уже было указано в части A1, измерения должны проводиться при комнатной температуре. Избегайте нагрева пьезопластинки руками.

Часть C. Температура Кюри пьезопластинки (4.0 балла)

У большинства диэлектриков диэлектрическая проницаемость не зависит от температуры. Однако, у свинцово-цинковой керамики, из которой изготовлена пьезопластинка, статическая относительная диэлектрическая проницаемость зависит от температуры по закону:
\[\varepsilon_r=A+\frac{B}{T-T_c}, \quad \text{при} \quad T>T_c  .\]
Здесь $A$ и $B$ – константы, не зависящие от температуры. Эта зависимость называется законом Кюри-Вейса. Параметры $B$ и $T_c$ называются, соответственно, константой Кюри и температурой Кюри в честь Пьера Кюри.
При температуре Кюри происходит фазовый переход. Выше температуры Кюри вещество находится в параэлектрической фазе, в которой элементарные диполи кристаллических ячеек вещества ориентированы хаотично. Ниже температуры Кюри элементарные диполи взаимодействуют друг с другом, создавая внутреннее поле, ориентирующее диполи. В кристалле возникает спонтанная поляризация при отсутствующем внешнем поле. Относительная диэлектрическая проницаемость ниже температуры Кюри описывается выражением:
\[\varepsilon_r=1+\frac{B}{2(T-T_c)}, \quad \text{при} \quad T<T_c  .\]
Из части A вам уже известно, что ε_r≫1, поэтому в выражении выше можно пренебречь единицей и считать, что:
\[\varepsilon_r=\frac{B}{2(T-T_c)}, \quad \text{при} \quad T<T_c  .\]
Таким образом ёмкость пьезопластинки, полученной в части A, изменяется с температурой. Так как температура Кюри пьезопластинки больше, чем температура кипения воды, мы оценим её при помощи линейной экстраполяции.
 

C1  ^1.50 Измерьте ёмкость пьезопластинки при различных температурах и заполните таблицу измерений.

C2  ^2.50 Проведите анализ полученных измерений, постройте график в разумных координатах и определите по нему температуру Кюри.

Часть D. Измерение скорости звука в алюминии (6.5 балла)

В твёрдых телах звук может быть как поперечным, так и продольной волной. Движения частиц твёрдого тела, соответствующие этим волнам, показаны на рисунке ниже.

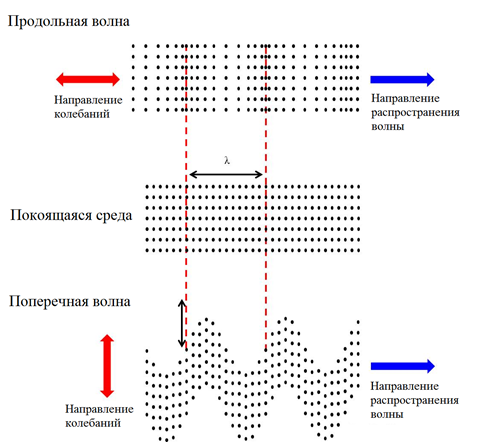
Продольные волны распространяются в твёрдых телах, жидкостях и газах, так как энергия переносится благодаря сжатиям и разрежениям среды.

В поперечных волнах смещение частиц среды перпендикулярно направлению распространения волны, поэтому поперечные волны не могут распространяться в жидкостях и газах.

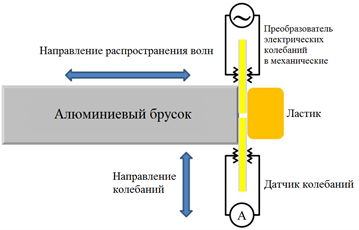
В этой части вам предлагается измерить скорости продольных и поперечных волн в алюминиевом бруске. Начните с измерения скорости поперечных колебаний, а потом перейдите к продольным.

D1  ^0.60 Введём обозначения: $L$ — длина бруска, $u$ — скорость волны.
Напишите выражения для частот $f_n$ стоячих (резонансных) волн, расположенных вдоль длинной стороны бруска при его незакреплённых концах. Выразите скорость $u$ через $f_n$.

D2  ^1.60

Измерьте рулеткой длину $L$ алюминиевого бруска. Повторите измерения несколько раз, найдите среднюю длину и стандартное отклонение.
Изменяя частоту звуковых волн, издаваемых первой пластинкой, найдите резонансные пики тока, протекающего через вторую пластинку. Постройте спектр резонансных частот по аналогии с графиком на рисунке.

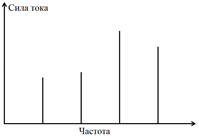
D3  ^1.40 Найдите резонансные пики силы тока для поперечных стоячих волн. Определите скорость поперечных волн в алюминии. Рассчитайте погрешности.

Внимание: вы можете получить пики, которые не имеют отношения к поперечным волнам, из-за несовершенства установки (например, неидеальности граничных условий). Вам нужно понять, какие пики не относятся к поперечным стоячим волнам при анализе результатов.

Если прижать пьезопластинки к бруску другим образом, можно измерить скорость продольных колебаний. Расположите пластинки относительно бруска так, как показано на рисунке ниже. Колебания вдоль длинной стороны пьезопластинки будут передаваться бруску, генерируя его продольные колебания

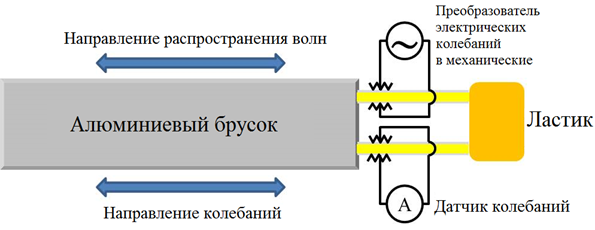
В части B упоминалось, что, хотя колебания пьезопластинки происходят преимущественно вдоль её длинной стороны, пластинка колеблется также и вдоль других направлений. Эти колебания могут передаваться бруску и приводить к появлению дополнительных резонансных пиков в спектре. Обратите внимание, что колебания вдоль других направлений будут возбуждать только поперечные волны. Таким образом, дополнительные резонансные пики не будут совпадать с резонансными пиками от продольных стоячих волн.

D4  ^1.50 Изменяя частоту звуковых волн, возбуждаемых первой пластинкой, найдите резонансные пики тока, протекающего через вторую пластинку. Постройте спектр резонансных частот.

D5  ^1.40 Сравнивая полученный спектр со спектром из п. D2, определите резонансные пики от поперечных волн. Выделите резонансные пики, соответствующие продольным волнам и найдите их скорость. Рассчитайте погрешности.

Часть E. Определение дефекта в алюминиевом бруске (2.0 балла)

После того, как вы определили скорость продольных волн в части D, вам предлагается определить местоположение искусственно созданного дефекта (глубокого плоского надпила) во втором алюминиевом бруске, закрытом непрозрачным экраном (чёрном ящике).
Звуковые волны активно используются для обнаружения скрытых трещин, полостей и других внутренних неоднородностей в металлах, композитных материалах, пластиках и керамике. Промышленное ультразвуковое тестирование проводится путём подачи короткого импульса частотой в несколько мегагерц и амплитудой в несколько сотен вольт на пьезоэлемент, который преобразует его в ультразвуковые колебания образца, и анализа усиленного полученного от него сигнала на предмет отражения от неоднородностей. Этот метод слишком сложен для нашей установки. Вместо этого в качестве демонстрации, мы воспользуемся уже знакомым методом резонанса для определения местоположения глубокого плоского надпила в бруске. В отличие от части D звуковые волны будут отражаться от места надпила, а не от дальнего конца бруска. Таким образом, расположение резонансных пиков на спектре будет отличаться от спектра из части D, что может помочь определить местоположение надпила.

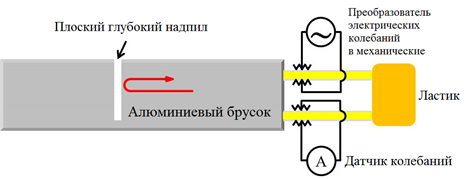
Используйте для этой части продольные стоячие волны.

E1  ^1.20 Изменяя частоту звуковых волн, издаваемых первой пластинкой, найдите резонансные пики тока, протекающего через вторую пластинку. Постройте спектр резонансных частот.

E2  ^0.80 На построенном графике отметьте резонансные пики, соответствующие продольным стоячим волнам, и найдите расстояние от надпила до края бруска, к которому прижимаются пьезопластинки.