В космических лучах обнаруживаются частицы, обладающие чрезвычайно большой энергией. Возможный механизм появления таких частиц называется ускорением Ферми. Ускорение Ферми — это стохастический механизм ускорения, которое заряженные частицы испытывают при многократном отражении, обычно от магнитного зеркала. В данной задаче рассматриваются основные идеи, лежащие в основе этого, парадоксального на первый взгляд, явления.

Почему встречных машин больше, чем попутных?

По автомагистрали, имеющей три полосы $A$, $B$, $C$, движутся с постоянной скоростью в одном направлении автомобили: по центральной полосе $B$ автомобиль движется со скоростью $v = 90~км/ч$; по полосе $A$ движутся автомобили со скоростями $v-\Delta v= 80~км/ч$; по полосе $C$ движутся автомобили со скоростями $v+\Delta v = 100~км/ч$. Расстояние между автомобилями одинаковое на каждой из полос $A$ и $C$, число автомобилей на единицу длины полосы для каждой из них составляет $n=5.0~км^{-1}$.

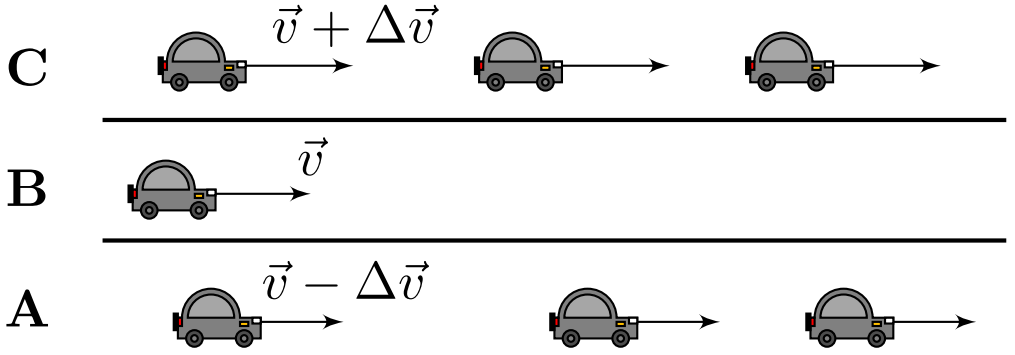
Рассмотрим автомобиль, движущийся по полосе $B$.

2.1  ^0.40 Рассчитайте, сколько автомобилей $N_{1}$, движущихся по полосе $A$, обгоняет автомобиль $B$ за время $t =1.0~мин$, а также время $\tau_{1}$ между двумя последовательными обгонами.

2.2  ^0.40 Рассчитайте, сколько автомобилей $N_{2}$, движущихся по полосе $C$, которые обгоняют автомобиль на полосе $B$ за время $t =1.0~мин$, а также время $\tau_{2}$ между двумя последовательными обгонами.

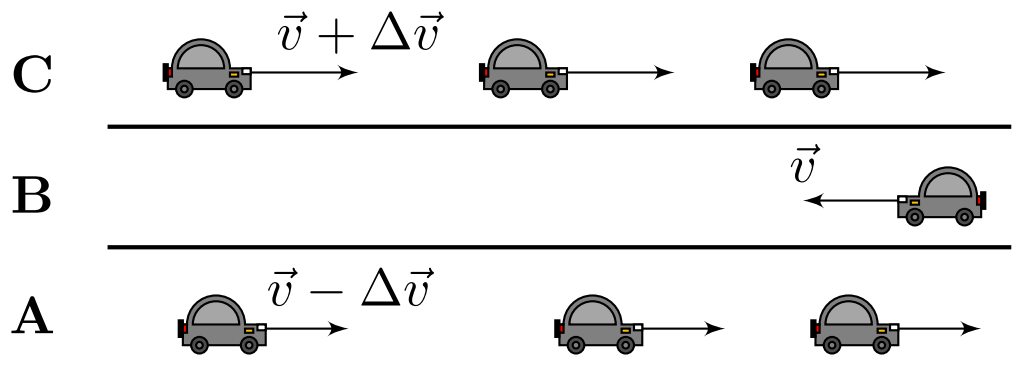
Пусть теперь автомобиль движется по полосе $B$ навстречу автомобилям, движущимся по полосам $A$ и $C$. Скорости автомобилей и их плотность на дороге остаются прежними.

2.3  ^0.80 Рассчитайте числа автомобилей $N_{3}$, движущихся по полосе $A$, и $N_{4}$, движущихся по полосе $C$, которые встречает автомобиль $B$ за время $t =1.0~мин$, а также соответствующие времена $\tau_{3}$ и $\tau_{4}$ между двумя последовательными встречами.

Упругое столкновение

В данной части рассмотрим классическую задачу об упругом столкновении двух тел. Основной целью данного рассмотрения является определение условий, при которых кинетическая энергия одного из выбранных тел возрастает в результате удара. Два упругих шарика, массы которых равны $m_{1}$ и $m_{2}$, движутся вдоль оси $x$. Скорость первого шарика до столкновения равна $v_{1}$, скорость второго — $v_{2}$. Обозначим скорости шариков после абсолютно упругого центрального столкновения $u_{1}$ и $u_{2}$, соответственно. Под скоростями шариков следует понимать проекции скоростей на ось $x$, поэтому они могут быть как положительными, так и отрицательными.

2.4  ^0.60 Выразите скорости шариков $u_{1}$ и $u_{2}$ после удара через их скорости до удара $v_{1}$ и $v_{2}$, а также массы шариков.

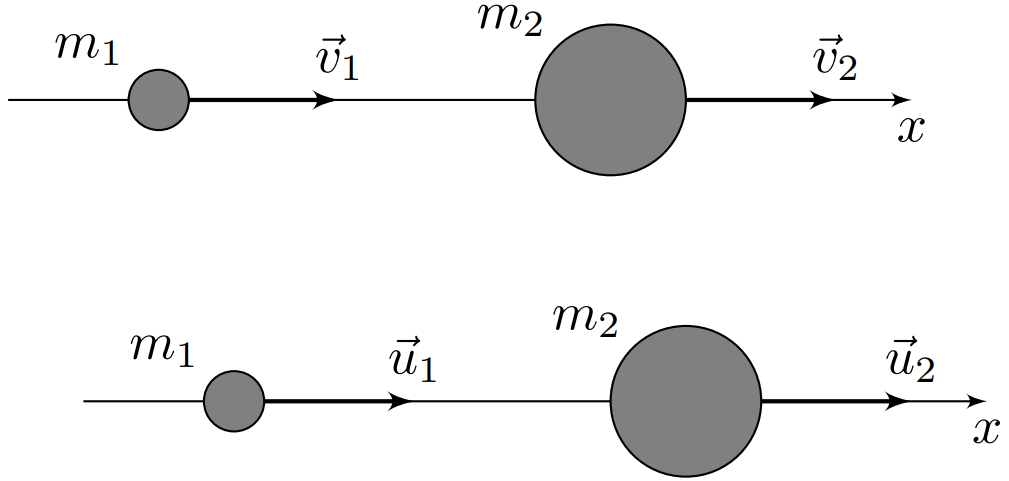
Обозначим отношение масс шариков как $\mu=\frac{m_{2}}{m_{1}}$, отношение скорости первого шарика после и до удара как $\eta_{1}=\frac{u_{1}}{v_{1}}$ и отношение скоростей шариков до удара как $\eta_{2}=\frac{v_{2}}{v_{1}}$. Для определенности считайте, что $v_{1} > 0$.

2.5  ^1.60 Постройте семейство графиков зависимостей параметра $\eta_{1}$ от параметра $\eta_{2}$ для всех характерных значений отношений масс шариков $\mu$.

2.6  ^0.40 Найдите соотношение между параметрами $\eta_{2}$ и $\mu$, при котором первый шарик увеличивает свою энергию в результате столкновения.

2.7  ^0.30 Рассмотрите случай столкновения легкого шарика с тяжелым $m_{2} \gg m_{1}$. Найдите в этом предельном случае скорость первого шарика после столкновения $\tilde{u}_{1}$ и определите область значений скоростей тяжелого шарика $\eta_{2}$ до столкновения, при которых энергия легкого шарика возрастает в результате столкновения.

Простейшая модель ускорения Ферми

Массивная плита, расположенная перпендикулярно оси $x$, совершает гармонические колебания в направлении оси $x$. Амплитуда колебаний равна $A$, их период — $T$. В направлении плиты вдоль оси $x$ с одинаковыми скоростями $u$ движутся легкие шарики. Времена подлета шариков к плите являются случайными и равномерно распределенными.

2.8  ^0.40 Выразите максимальную скорость движения плиты $V_{0}$ через амплитуду и период ее колебаний.

2.9  ^2.70 Рассчитайте долю $\varphi$ налетающих шариков, которые после столкновения увеличат свою кинетическую энергию. Ответ выразите через $u$ и $V_{0}$. Для численной оценки отдельно рассмотрите два случая: $а)$ $u =1.5 V_{0}$; $б)$ $u= 0.50 V_{0}$.

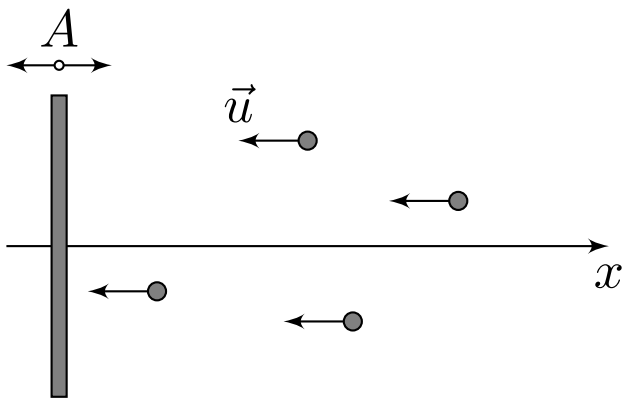
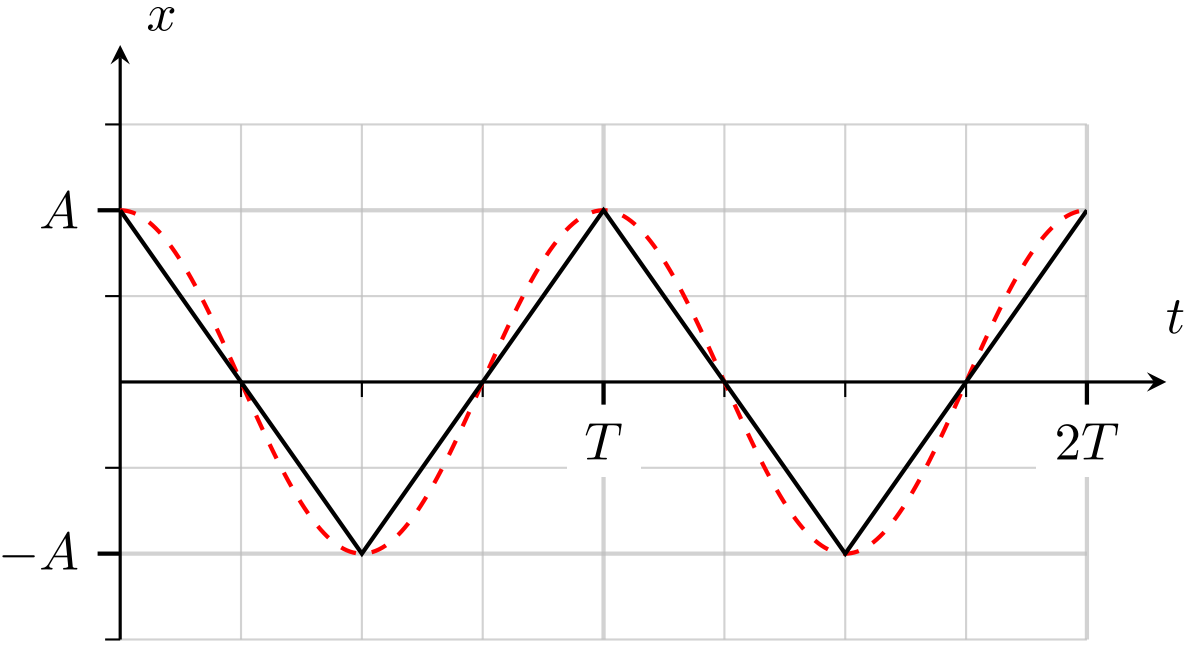
Аппроксимируем гармонический закон движения плиты кусочно-линейной функцией, смотрите рисунок ниже, то есть будем считать, что модуль скорости $V$ движения плиты остается постоянным при тех же значениях амплитуды и периода колебаний.

2.10  ^0.20 Выразите значение модуля скорости движения плиты $V$ через амплитуду и период ее колебаний.

2.11  ^2.20 Рассчитайте, во сколько раз изменится средняя энергия налетающих шариков $\varepsilon =\frac{E}{E_{0}}$, где $E_{0}$ — кинетическая энергия шариков до столкновения, $E$ — средняя энергия шариков после столкновения с колеблющейся плитой. Для численной оценки отдельно рассмотрите два случая: $а)$ $u =1.5 V$; $б)$ $u= 0.50 V$.