

В настоящий момент Международная Космическая Станция (сокращённо МКС, англ. ISS — International Space Station) двигается по орбите, близкой к круговой. Минимальное среднее расстояние до Земли при её движении составляет $370~км$, максимальное — $460~км$. Станция двигается в термосфере. Плоскость орбиты составляет угол $\theta = 51.6^\circ$ с плоскостью экватора. Траектория станции похожа на спираль с медленно меняющимся расстоянием от неё до поверхности Земли. Изменение данного расстояния за один оборот вокруг Земли незначительно.
Масса МКС составляет $M_s = 4.5 \times 10^5~кг$, общая длина $L_s = 109~м$. Огромные солнечные панели шириной $W_S = 73~м$ обеспечивают МКС электрической энергией [Официальный Отчёт NASA (2023)].
С учётом всех батарей и других частей, эффективная площадь поперечного сечения станции составляет приблизительно $S \approx 2.5 \times 10^3~м^2$ [Европейское Космическое Агентство, SDC6-23].
Снижение орбиты МКС связано с несколькими явлениями, уменьшающими энергию орбитального движения. Основными из них являются:
"... В мае 2008 высота орбиты МКС составляла 350 километров, станция потеряла 4.5 км высоты, а затем с помощью транспортного грузового космического корабля Прогресс М-64 была поднята на 5.5 км ..." [https://mod.jsc.nasa.gov]
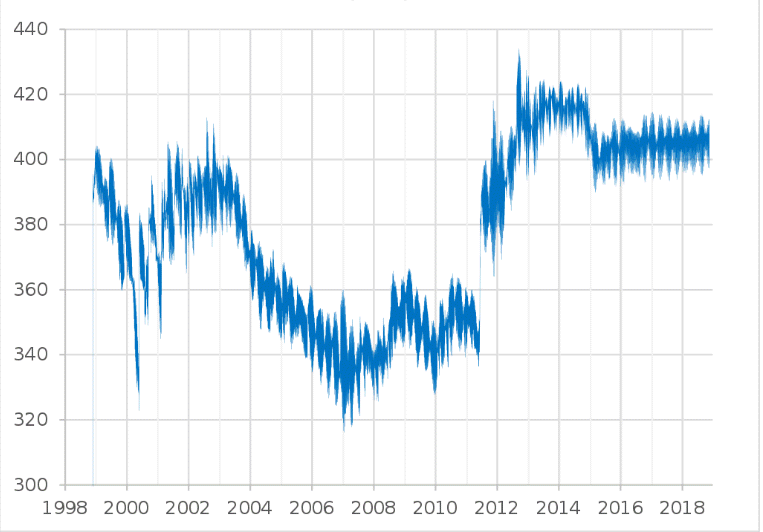
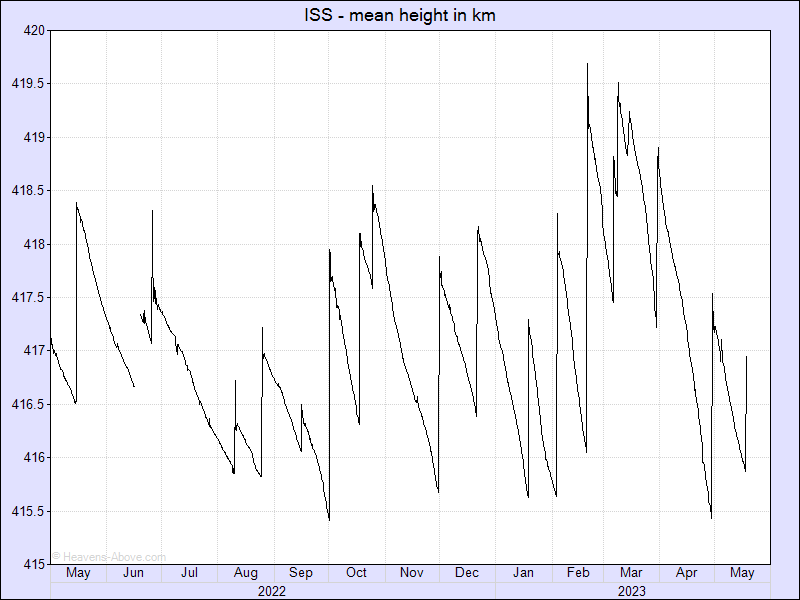
"... МКС теряет до 100 м высоты каждый день... " [Данные NASA (2021)]. В 2023 году МКС движется на высоте 410 км, и снижается приблизительно на 70 м в день ($\sim$ 2 км в месяц). Во время магнитных бурь снижение достигает 300 м. МКС корректирует свою орбиту с помощью своих двигателей, а также двигателей посещающих её аппаратов [Отчёт о МКС (2022)].
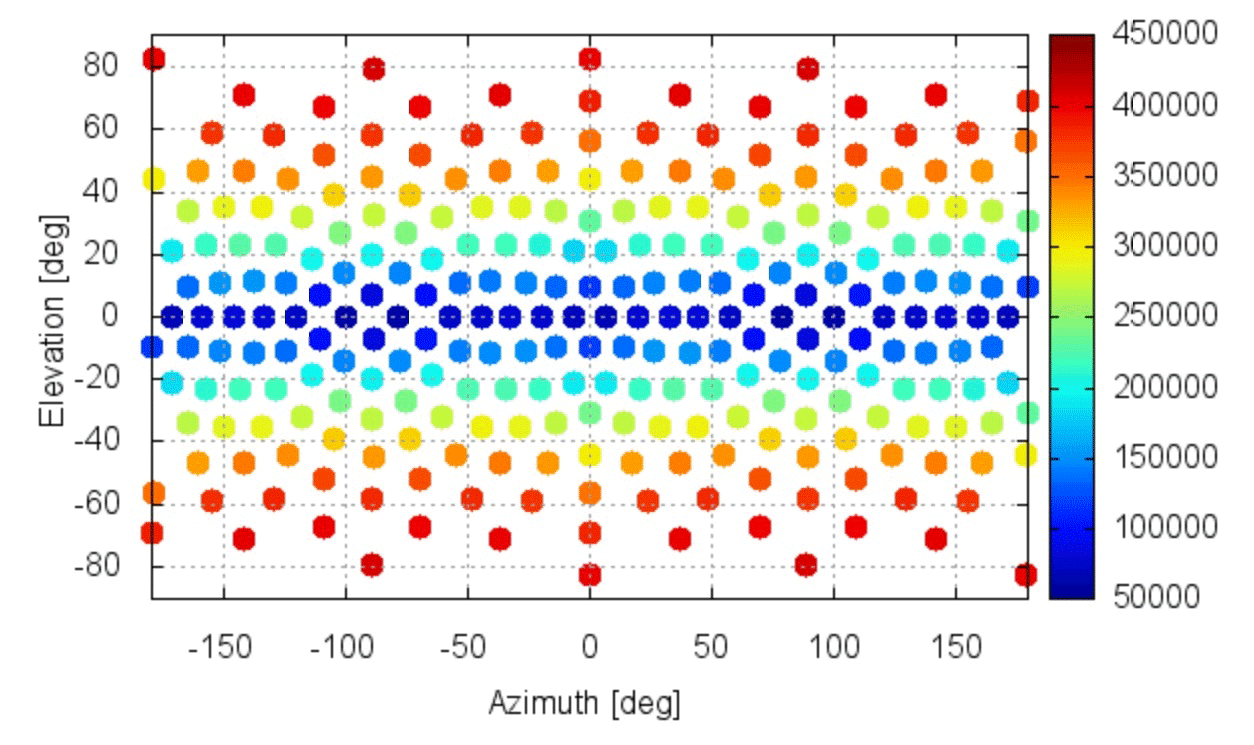
Универсальная газовая постоянная $R$ $=$ $8.31~$Дж$\cdot$К$^{-1} \cdot $моль$^{-1}$ Число Авогадро $N_A$ $=$ $6.022 \cdot 10^{23}~$моль$^{-1}$ Молярная масса воздуха $\mu$ $=$ $0.029~$кг$\cdot$моль$^{-1}$ Масса Земли $M_E$ $=$ $5.97 \cdot 10^{24}~$кг Радиус Земли $R_E$ $=$ $6.38 \cdot 10^6~$м Гравитационная постоянная $G$ $=$ $6.67 \cdot 10^{-11}~$м$^3 \cdot$с$^{-2} \cdot$кг$^{-1}$ Плотность воздуха на поверхности Земли $\rho_0$ $=$ $1.29~$кг$/$м$^3$ Ускорение свободного падения на поверхности Земли $g_0$ $=$ $9.81~$м$\cdot$с$^{-2}$ Средняя величина магнитного поля Земли $B$ $=$ $5.0 \cdot 10^{-5}~$Тл Модуль заряда электрона $e$ $=$ $1.60 \cdot 10^{-19}~$Кл
Воздух в атмосфере состоит по большей части из нейтральных молекул $O_2$ и $N_2$. Воздух подчиняется уравнению Менделеева-Клапейрона: $pV = \frac{M}{\mu} RT$, где $p$, $V$, $T$, $M$ и $\mu$ это давление, объём, температура, масса и молярная масса порции газа соответственно, $R$ — универсальная газовая постоянная.
Есть два уравнения для вычисления зависимости давления воздуха от высоты. Первое уравнение применимо к стандартной модели тропосферы (высоты $h<100~$км). Оно предполагает изменение температуры с высотой.
Второе уравнение относится к стандартной модели термосферы ($h>250~$км). В нём температура почти не зависит от высоты. Это уравнение применимо к исследованию движения МКС.
В этой задаче можно считать давление гидростатическим и изотропным (то есть оно действует одинаково по всем направлениям).
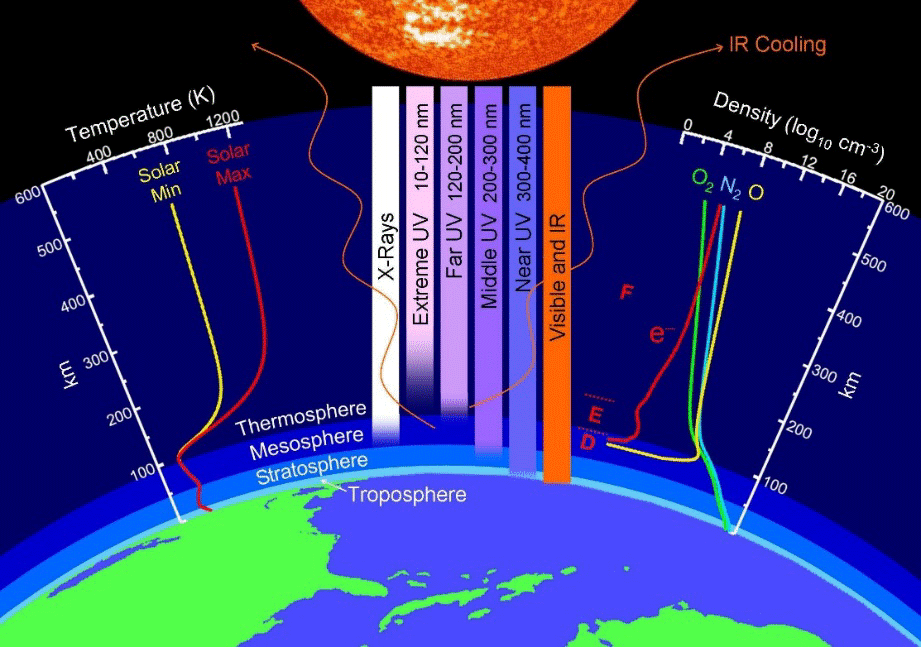
Примечание 1. Температура термосферы Земли на высотах $300 - 600~$км меняется незначительно и в среднем составляет $800 - 900~$К на солнечной стороне [Данные NASA]. Следовательно, при исследовании полёта МКС мы можем считать $T_h = T = const$. Так как космический корабль проводит почти половину времени полёта с теневой стороны Земли, где температура резко снижается, можно считать, что в среднем на этих высотах температура равна $T = 425~$К.
Эта температура также соответствует значению плотности воздуха $\rho_h \sim 10^{-12}~$кг$/$м$^3$ на высоте $h = 400~$км [Модель Верхних Слоёв Атмосферы Земли MSISE-90].
Пусть на станцию массой $M_S$ действует постоянная тормозящая сила $\vec{F}_{drag}$. В этой части задачи оценивается скорость уменьшения высоты орбиты МКС. Считайте, что изменение высоты $dh$ значительно меньше высоты полёта $h$ ($dh \ll h$).
Скорость станции $v$ во много раз больше чем средние скорости (сотни м$/$с) теплового движения молекул в атмосфере на высоте $h \approx 300 - 400~$км, то есть можно считать, что молекулы покоятся перед столкновением с МКС. Для грубой оценки считайте, что после столкновения молекулы приобретают такую же скорость, что и станция.
В термосфере под действием излучения воздух ионизируется (из-за чего, например, возникает «северное сияние»). В отличие от кислорода $O_2$, азот $N_2$ не диссоциирует под действием солнечного излучения, поэтому в верхних слоях атмосферы атомарного азота $N$ гораздо меньше, чем атомарного кислорода $O$. На высотах больше $250~$км преобладает атомарный кислород $O$. Слои, содержащие электроны и ионы атомов кислорода, возникают на освещенной стороне атмосферы. В этом случае концентрация ионов атомарного кислорода составляет $n_{ion} \sim 10^{12}~м^{-3}$.
Рассмотрим влияние магнитного поля Земли на движение станции. Магнитное поля Земли вблизи поверхности изменяется в диапазоне $(3.5 - 6.5) \cdot 10^{-5}~$Тл , среднее значение составляет $B = 5 \cdot 10^{-5}~$Тл.
Когда станция движется с большой скоростью в магнитном поле, в её проводящих элементах возникает электрический ток. Электродвижущая сила вызывает перераспределение электрических зарядов в проводящих элементах станции. Электрическое поле вблизи станции приводит к движению заряженных частиц в окружающем её пространстве. Электроны притягиваются к частям станции, у которых положительный потенциал (относительно средней части станции), а ионы притягиваются к частям с отрицательным потенциалом. Электроны и ионы, сталкиваясь с поверхностью станции, стремятся собираться в нейтральные атомы кислорода. Эти электроны, которые движутся по проводящим частям станции, и создают электрический ток. Станция, двигаясь в космосе, «собирает» электроны и ионы из окружающего пространства, сталкиваясь с ними.
Для грубой оценки тока, возникающего в проводящих частях станции, считайте, что она «собирает» частицы только с площади, эквивалентной площади поперечного сечения станции $S$. Также считайте, что все ионы и электроны участвуют в создании тока.
E2
0.60
Получите приближённое выражение для тормозящей силы Ампера $F_{ind}$ в направлении, противоположном направлению движению станции.
Пусть $\phi$ — угол между магнитным полем Земли $\vec{B}$, направленным вдоль меридианов, и скоростью МКС $\vec{v}$. Для простоты считайте, что длина станции $L$ равна корню квадратному из её площади $S$. Кроме того, вместо подсчёта среднего значения $\sin(\phi)$ вы можете аппроксимировать его значением $\sin(\pi/2 - \theta)$. Вы можете использовать дискретное число точек для подсчёта среднего значения.