Кавитация — это явление образования пузырьков с паром или «полостей» (англ. cavity) в жидкой среде из-за понижения давления. Этим кавитация отличается от кипения, при котором пузырьки возникают за счет увеличения температуры. Когда давление снова повышается, пузырьки с паром схлопываются и создают ударные волны и сверхзвуковые струи.

Кавитация как правило происходит из-за микроскопических пузырьков, кавитационных зародышей, которые всегда есть в жидкости. Размер этих микропузырьков порядка нескольких микрон, они содержат как воздух, так и пар. Если давление в жидкости становится достаточно маленьким, зародыш увеличивается до макроскопического размера, начинается кавитация. Если очистить жидкость от таких зародышей, кавитация не начнется даже при отрицательном давлении.
В этой задаче изучаются идеализированные модели кавитации. Один из параметров, которые можно определить — критическое (или пороговое) давление, то есть минимальное значение давления воды, при котором зародыши не увеличиваются до макроскопических размеров. Критическое давление приближенно равно давлению водяного пара при заданной температуре, но его точное значение несколько ниже из-за поверхностного натяжения и воздуха в зародыше.
Если внешнее давление внезапно уменьшится и станет меньше критического давления, зародыш начнет расширяться и скорость расширения быстро достигнет установившегося значения. Обычно к тому времени, когда пузырек достигает макроскопического размера, давление возвращается к исходному значению, и пузырек начинает схлопываться.
Рассмотрим следующую модель: макроскопический пузырек находится в равновесии, а давление внезапно повышается. Тогда если внутри пузырька есть воздух, он сначала схлопнется, а затем начнет расширяться, достигнув некоторого минимального размера. Если же пузырек содержит только водяной пар, он полностью исчезнет, причем скорость сжатия пузырька будет неограниченно возрастать, когда его размер стремится к 0.
На самом деле в конце схлопывания пузырек не будет сферическим и нужно будет учитывать сжимаемость воды. Однако если не сказано обратного, этими эффектами можно пренебречь.
Когда звуковая волна проходит через воду с пузырьками, эта волна заставляет пузырьки пульсировать за счет изменения давления, а также вызывает поступательное движение пузырьков.
Теория предсказывает, что из-за диффузии воздуха через границу пузырька, он полностью растворится, если только раствор воздуха в воде не насыщенный. Однако на самом деле в воде существуют зародыши микронного размера, и от них крайне сложно избавиться. Поэтому само существование зародышей представляет собой парадокс. Рассмотрим одно из возможных разрешений этого парадокса, а именно предположение, что маленькие полости в стенках или твердых частицах содержат микроскопические объемы воздуха и пара.
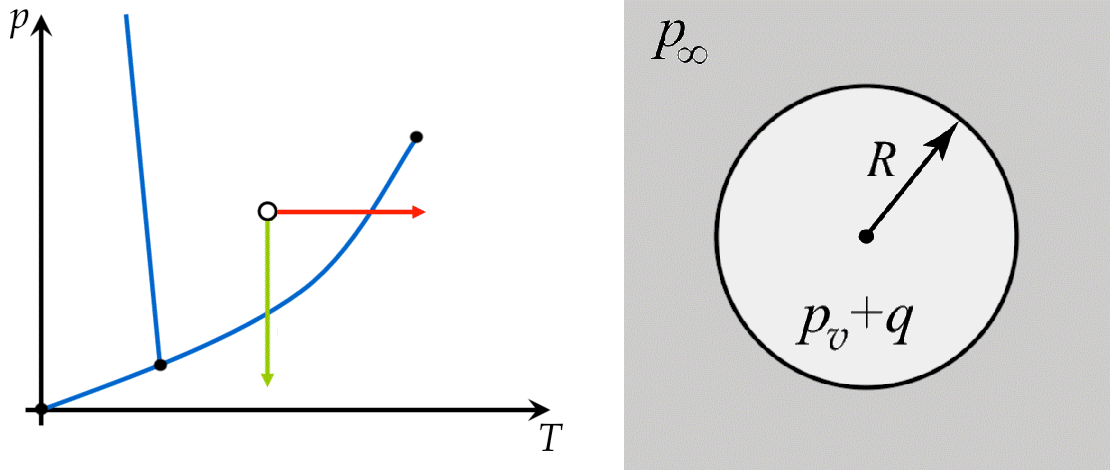
Рассмотрим замкнутый сосуд, содержащий воду и воздух. Если воздух слишком сухой, его влажность будет возрастать за счет испарения воды. Если воздух слишком влажный, его влажность уменьшится за счет конденсации. Оказывается, что в равновесии парциальное давление водяного пара $p_v=p_v(T)$ — функция температуры.
Если объем пузырька мгновенно изменяется, влажность внутри пузырька выйдет из равновесия с окружающей водой, и система должна прийти в новое положение равновесия путем испарения или конденсации. В реальности этот процесс настолько быстрый, что мы можем считать, что пар все время находится в равновесии. Поскольку количеством тепла, которое получает или отдает окружающая вода в этом процессе, можно пренебречь, температура остается постоянной. Поэтому можно считать, что парциальное давление пара в пузырьке все время остается равным $p_v$.
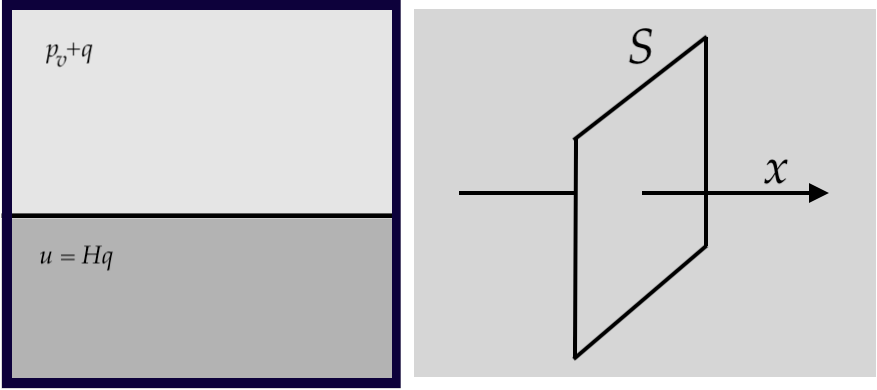
Закон Генри позволяет описывать поведение воздуха в пузырьке. Он утверждает, что концентрация воздуха, растворенного в воде, в равновесии пропорциональна давлению воздуха над поверхностью воды:
\begin{equation*}u=Hq,\end{equation*}
где $u$ — концентрация воздуха в воде, $H$ — постоянная Генри, $q$ — парциальное давление воздуха над поверхностью воды. Как и раньше, будем считать, что воздух в пузырьке находится в равновесии и не происходит никаких изменений температуры.
Растворенный в воде воздух перемещается из областей с высокой концентрацией в области с низкой концентрацией. Закон Фика утверждает, что поток за счет диффузии через элемент поверхности $S$ пропорционален скорости изменения концентрации в направлении, перпендикулярном к $S$:
\begin{equation*} J = \kappa \frac{\partial u}{\partial x} \end{equation*}
Здесь $J$ — диффузионный поток, количество молекул воздуха, которые проходят через единицу площади поверхности в единицу времени, $\kappa$ — коэффициент диффузии, координата $x$ перпендикулярна $S$. Если $u$ — функция $x$ и возможно других переменных, обозначение $\dfrac{\partial u}{\partial x}$ означает производную по $x$, при постоянных остальных переменных.
Если вам нужно найти функцию $w = w(x,t)$ в первой координатной четверти $Q$ (то есть при $x>0$ и $t>0$), которая удовлетворяет в $Q$ уравнению
\begin{equation*}\frac{\partial w}{\partial t} = \frac{\partial^2 w}{\partial x^2},\end{equation*}
а также условиям
\begin{cases}
w(x,0) = f(x), \quad x>0, \\
w(0,t) = 0, \quad t>0,
\end{cases}
то решение имеет вид
\begin{equation*}w(x,t) = \frac1{\sqrt{4\pi t}}\int_0^\infty \big( e^{-(x-y)^2/(4t)} - e^{-(x+y)^2/(4t)} \big) f(y) dy .\end{equation*}
Вам могут потребоваться следующие интегралы:
\begin{equation*}\int_0^\infty e^{-bx^2} dx = \frac{\sqrt\pi}{2\sqrt{b}},\qquad \int_0^\infty x^2e^{-bx^2} dx = \frac{\sqrt{\pi}}{4b\sqrt{b}} \qquad (b>0). \end{equation*}
В таблице 1 приводится список обозначений, используемых в задаче, и стандартные значения некоторых постоянных
Символ Значение Стандартное численное значение $\rho$ плотность воды $997$ кг/м$^3$ $p_{\infty}$ давление воды вдали от пузырька $101$ кПа $p_v$ давление пара $2340$ Па $\sigma$ коэффициент поверхностного натяжения воды $72.8\cdot10^{-3}$ Н/м $R$ радиус пузырька $R_0$ начальный радиус пузырька $10^{-5}$ м $\delta$ плотность воздуха $1.29$ кг/м$^3$ $q$ парциальное давление воздуха в пузырьке $q_0$ начальное значение $q$ $\gamma$ показатель адиабаты воздуха $1.4$ $u$ концентрация растворенного воздуха в воде $\kappa$ коэффициент диффузии воздуха в воде $2 \cdot 10^{-9}$ м$^2$/с $H$ постоянная Генри для воздуха в воде $0.24\cdot 10^{-6}$ с$^2$/м$^2$ $t$ время $f_0$ собственная/резонансная частота
Если не указано обратное, используйте следующие предположения.
A1
0.50
Используя метод размерностей, оцените время $T$ схлопывания пузырька, содержащего только пар. Выразите ответ через начальный радиус пузырька $R_0$, плотность воды $\rho$, давление воды $p_{\infty}$ и давление пара $p_v$.
Найдите численное значение времени, считая, что коэффициент пропорциональности в полученной формуле равен 1, $R_0 = 1$ мм, а значения $\rho$, $p_{\infty}$, и $p_v$ возьмите из таблицы обозначений. Поверхностное натяжение не учитывайте, $\sigma = 0$.
A2
1.00
Пусть пузырек радиуса $R_0 = 10^{-5}$ м, состоящий из воздуха и пара, находится в равновесии, когда внешнее давление равно $p_{\infty} = 101 $ кПа. Найдите парциальное давление $q_0$ воздуха в пузырьке.
Пусть теперь внешнее давление $p_\infty$ постепенно уменьшают, а процесс для воздуха в пузырьке изотермический. Найдите критическое давление $p_c$, которое определяется тем условием, что при $p_{\infty} < p_c$ размер пузырька неограниченно возрастает. Значения $p_v$ и $\sigma$ считайте равными их стандартным значениям из таблицы обозначений.
Изучим динамику сферического пузырька, содержащего смесь воздуха и пара. Считайте, что воздух не перемещается через границу пузырька и поэтому для описания поведения пузырька достаточно определить давление в нем.
Тем не менее испарение и конденсация пара будет происходить на стенках пузырька, и эти процессы поддерживают давление пара $p_v$ внутри пузырька.
B1
1.50
Пусть один сферический пузырек находится в воде, которая заполняет все пространство. Пузырек может менять размер (например из-за изменения внешнего давления $p_{\infty}$), при этом все время оставаясь сферическим.
Получите уравнение, которое связывает радиус пузырька $R(t)$ и его производные по времени $R'(t)$ и $R''(t)$, поверхностное натяжение $\sigma$, плотность воды $\rho$, давление вдали от пузырька $p_{\infty}$, и давление внутри пузырька $p$.
Затем разбейте давление $p$ внутри пузырька на два слагаемых, считая, что пузырек содержит пар (с парциальным давлением $p_v$) и воздух. Процесс для воздуха адиабатический, показатель адиабаты $\gamma$. Начальное давление воздуха $q_0$, начальный радиус пузырька $R_0$.
Считайте, что испарение, конденсация, или перенос воздуха между пузырьком и окружающей его водой не влияют на объем воды.
B2
1.00
Бак с водой с давлением $p_{\infty}^{-} = 101$ кПа содержит пузырек радиуса $R_0 = 10^{-5}$ м, изначально находящийся в состоянии равновесия. В некоторый момент времени давление мгновенно уменьшается до $p_{\infty} = 0$. Оцените предельное (асимптотическое) значение скорости роста пузырька $R'$, а также время, за которое скорость достигнет этого значения.
B6
1.00
Пусть пузырек, описанный в предыдущем пункте, находится в области, в которой есть стоячая звуковая волна. Давление в волне меняется вдоль оси $x$ как
\begin{equation*} p(x,t) = p_0 + A \sin\left(\frac{2\pi f}{c}(x+a)\right) \sin(2\pi ft) , \end{equation*}
где $f$ — частота, $c$ — скорость звука. Параметры $p_0$, $A$ и $a$ — постоянные, смысл которых можно понять из уравнения.
Найдите среднюю силу, действующую на пузырек. Он расположен в начале системы координат $xyz$, его размер много меньше длины волны звука.
В этой части рассмотрим диффузию воздуха через границу пузырька.
C1
2.00
Пусть пузырек радиуса $R_0 = 10^{-5}$ м, содержащий воздух и пар, находится в растворе воздуха в воде, в котором растворенный воздух находится в равновесии с воздухом при атмосферном давлении.
Парциальное давление воздуха в пузырьке $q = 1.70\cdot 10^5$ Па, давлением пара можно пренебречь. Оцените время, за которое пузырек полностью растворится в воде.
Значения величин $p_{\infty}$, $\kappa$, $\delta$ и $\sigma$ возьмите в таблице 1. Считайте, что область вокруг пузырька, в которой происходит диффузия воздуха, мгновенно становится много больше самого пузырька.