A1  ^0.50 Используя метод размерностей, оцените время $T$ схлопывания пузырька, содержащего только пар. Выразите ответ через начальный радиус пузырька $R_0$, плотность воды $\rho$, давление воды $p_{\infty}$ и давление пара $p_v$.

Найдите численное значение времени, считая, что коэффициент пропорциональности в полученной формуле равен 1, $R_0 = 1$ мм, а значения $\rho$, $p_{\infty}$, и $p_v$ возьмите из таблицы обозначений. Поверхностное натяжение не учитывайте, $\sigma = 0$.

A1. 1 Получение формулы$ \tau \sim R_0 \sqrt{\dfrac{\rho}{p_\infty - p_v}} $	0.40
A1. 2 Численный ответ $ \tau \approx 0.1 ~\text{мс} $	0.10

A2  ^1.00 Пусть пузырек радиуса $R_0 = 10^{-5}$ м, состоящий из воздуха и пара, находится в равновесии, когда внешнее давление равно $p_{\infty} = 101 $ кПа. Найдите парциальное давление $q_0$ воздуха в пузырьке.

Пусть теперь внешнее давление $p_\infty$ постепенно уменьшают, а процесс для воздуха в пузырьке изотермический. Найдите критическое давление $p_c$, которое определяется тем условием, что при $p_{\infty} < p_c$ размер пузырька неограниченно возрастает. Значения $p_v$ и $\sigma$ считайте равными их стандартным значениям из таблицы обозначений.

A2. 1 Условие, связывающее давление в равновесии $ p_v + q = p_\infty + \frac{2 \sigma}{R}, $	0.30
A2. 2 Численный ответ для давления воздуха $ q_0 \approx 170 ~\text{кПа}. $	0.10
A2. 3 Условие равновесия, уравнение изотермы $ q_0 R_0^3 = q R^3, $	0.10
A2. 4 Формула для критического давления $ p_c = p_v - 2 q_0 \left( \frac{R_0}{R_c}\right)^3 $ (возможно в других переменных)	0.40
A2. 5 Численный ответ для критического давления $p_c \approx 700~\text{Па}$	0.10

B1  ^1.50 Пусть один сферический пузырек находится в воде, которая заполняет все пространство. Пузырек может менять размер (например из-за изменения внешнего давления $p_{\infty}$), при этом все время оставаясь сферическим.

Получите уравнение, которое связывает радиус пузырька $R(t)$ и его производные по времени $R'(t)$ и $R''(t)$, поверхностное натяжение $\sigma$, плотность воды $\rho$, давление вдали от пузырька $p_{\infty}$, и давление внутри пузырька $p$.

Затем разбейте давление $p$ внутри пузырька на два слагаемых, считая, что пузырек содержит пар (с парциальным давлением $p_v$) и воздух. Процесс для воздуха адиабатический, показатель адиабаты $\gamma$. Начальное давление воздуха $q_0$, начальный радиус пузырька $R_0$.

Считайте, что испарение, конденсация, или перенос воздуха между пузырьком и окружающей его водой не влияют на объем воды.

B1. 1 Условие несжимаемости $ v(r,t) = \frac{R^2}{r^2} u(t), $	0.30
B1. 2 Вычисление радиального ускорения $ a = \frac{\partial v}{\partial t} + v \frac{\partial v}{\partial r} = \frac{R^2}{r^2} u' + \frac{2R}{r^2} u^2 - \frac{2 R^4}{r^5} u^2. $	0.50
B1. 3 Второй закон Ньютона $ \rho a = - p', $	0.30
B1. 4 Окончательное уравнение с $p$, в которое входит поверхностное натяжение	0.20
B1. 5 Окончательное уравнение, в котором $p$ разбито на сумму слагаемых и учтено уравнение адиабаты	0.20

B2  ^1.00 Бак с водой с давлением $p_{\infty}^{-} = 101$ кПа содержит пузырек радиуса $R_0 = 10^{-5}$ м, изначально находящийся в состоянии равновесия. В некоторый момент времени давление мгновенно уменьшается до $p_{\infty} = 0$. Оцените предельное (асимптотическое) значение скорости роста пузырька $R'$, а также время, за которое скорость достигнет этого значения.

B2. 1 Формула для конечной скорости	0.40
B2. 2 Численное значение конечной скорости	0.10
B2. 3 Формула для времени или начального ускорения	0.40
B2. 4 Численный ответ для времени	0.10

B3  ^1.00 Бак с водой с давлением $p_{\infty}^{-} = 1.600$ кПа содержит пузырек радиуса $R_0 = 10^{-5}$ м, изначально находящийся в состоянии равновесия. В некоторый момент времени давление стало равно $p_{\infty} = 101$ кПа. Оцените минимальный радиус пузырька перед тем, как он начнет расширяться.

B3. 1 Формула для скорости $R'$	0.50
B3. 2 Формула для минимального радиуса	0.40
B3. 3 Численный ответ для минимального радиуса	0.10

B4  ^0.50 Если внутри пузырька находится только водяной пар, пузырек полностью схлопнется за конечное время. Определите показатель степени $\alpha$ в зависимости
\begin{equation*} R(t)\sim(T-t)^{\alpha}, \end{equation*}
где $T$ — время схлопывания.

B4. 1 Асимптотическое уравнение для $R'$	0.20
B4. 2 Решение нужного вида подставлено в уравнение	0.20
B4. 3 Численное значение $\alpha$	0.10

B5  ^1.00 Используя уравнение, полученное в B3, найдите собственную частоту сферически-симметричных колебаний пузырька радиуса $R_0 = 0.1$ мм.

B5. 1 Записано линейное уравнение второго порядка	0.40
B5. 2 Записано условие устойчивости	0.20
B5. 3 Формула для собственной частоты	0.30
B5. 4 Численное значение собственной частоты	0.10

B6  ^1.00 Пусть пузырек, описанный в предыдущем пункте, находится в области, в которой есть стоячая звуковая волна. Давление в волне меняется вдоль оси $x$ как
\begin{equation*} p(x,t) = p_0 + A \sin\left(\frac{2\pi f}{c}(x+a)\right) \sin(2\pi ft) , \end{equation*}
где $f$ — частота, $c$ — скорость звука. Параметры $p_0$, $A$ и $a$ — постоянные, смысл которых можно понять из уравнения.

Найдите среднюю силу, действующую на пузырек. Он расположен в начале системы координат $xyz$, его размер много меньше длины волны звука.

B6. 1 Записано уравнение вынужденных колебаний	0.20
B6. 2 Решение уравнения	0.30
B6. 3 Вычисление объема	0.10
B6. 4 Вычисление градиента давления	0.10
B6. 5 Окончательный ответ	0.30

C1  ^2.00 Пусть пузырек радиуса $R_0 = 10^{-5}$ м, содержащий воздух и пар, находится в растворе воздуха в воде, в котором растворенный воздух находится в равновесии с воздухом при атмосферном давлении.

Парциальное давление воздуха в пузырьке $q = 1.70\cdot 10^5$ Па, давлением пара можно пренебречь. Оцените время, за которое пузырек полностью растворится в воде.

Значения величин $p_{\infty}$, $\kappa$, $\delta$ и $\sigma$ возьмите в таблице 1. Считайте, что область вокруг пузырька, в которой происходит диффузия воздуха, мгновенно становится много больше самого пузырька.

C1. 1 Начальная концентрация воздуха в воде	0.10
C1. 2 Начальная концентрация воздуха рядом с пузырьком	0.10
C1. 3 Скорость изменения массы в сферической оболочке, выраженная через скорость изменения концентрации	0.10
C1. 4 Скорость изменения массы в сферической оболочке, выраженная через потоки	0.10
C1. 5 Использован закон Фика	0.10
C1. 6 Уравнение диффузии в переменных $r$, $t$	0.20
C1. 7 Начальное и граничное условия	2 × 0.10
C1. 8 Переформулировка в терминах одномерной задачи и решение	0.20
C1. 9 Вычисление потока через стенку пузырька	0.20
C1. 10 Упрощение с учетом малости размера пузырька	0.10
C1. 11 Масса пузырька выражена через давление с учетом уравнения состояния идеального газа	0.20
C1. 12 Баланс масс	0.10
C1. 13 Окончательная формула для времени растворения	0.20
C1. 14 Численное значение времени растворения	0.10

C2  ^0.50

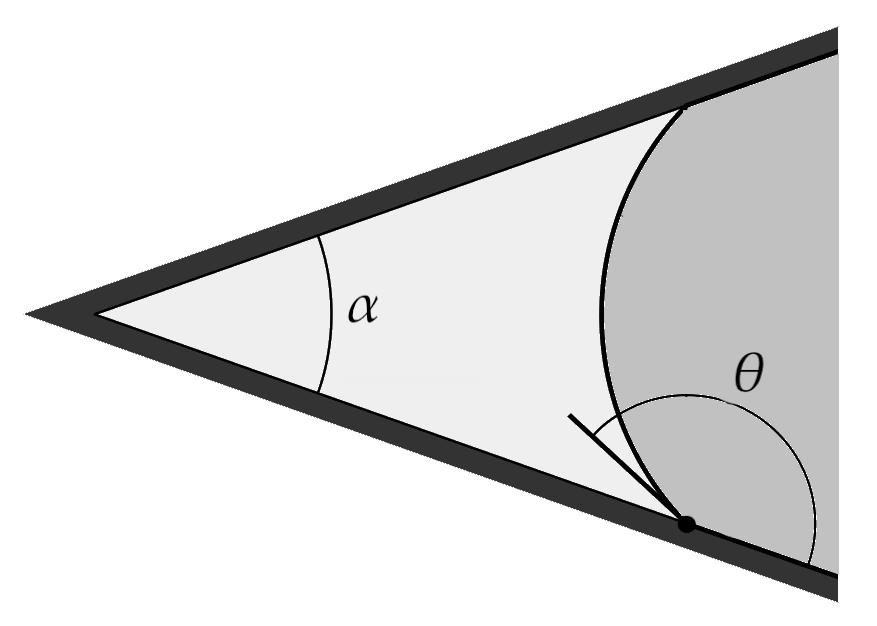
C2. 1 Условие равновесия	0.20
C2. 2 Окончательное условие на углы	0.30