A1  ^0.50 Используя метод размерностей, оцените время $T$ схлопывания пузырька, содержащего только пар. Выразите ответ через начальный радиус пузырька $R_0$, плотность воды $\rho$, давление воды $p_{\infty}$ и давление пара $p_v$.

Найдите численное значение времени, считая, что коэффициент пропорциональности в полученной формуле равен 1, $R_0 = 1$ мм, а значения $\rho$, $p_{\infty}$, и $p_v$ возьмите из таблицы обозначений. Поверхностное натяжение не учитывайте, $\sigma = 0$.

Естественно предположить, что пузырек не схлопнется если $p_\infty \le p_v$. Поэтому будем считать, что $p_\infty > p_v$, а время схлопывания будет зависеть только от разности $p_\infty - p_v$. Размерности используемых величин
$$
[R_0] = \text{м}, \; [\rho] = \text{кг}/\text{м}^3, \; [p_\infty - p_v] = \text{кг}/(\text{м}\cdot \text{с}^2).
$$
Из них можно составить единственную комбинацию с размерностью времени

A2  ^1.00 Пусть пузырек радиуса $R_0 = 10^{-5}$ м, состоящий из воздуха и пара, находится в равновесии, когда внешнее давление равно $p_{\infty} = 101 $ кПа. Найдите парциальное давление $q_0$ воздуха в пузырьке.

Пусть теперь внешнее давление $p_\infty$ постепенно уменьшают, а процесс для воздуха в пузырьке изотермический. Найдите критическое давление $p_c$, которое определяется тем условием, что при $p_{\infty} < p_c$ размер пузырька неограниченно возрастает. Значения $p_v$ и $\sigma$ считайте равными их стандартным значениям из таблицы обозначений.

В равновесии давления должны быть связаны условием (давление внутри пузырька больше давления на бесконечности за счет поверхностного натяжения)
$$
p_v + q = p_\infty + \frac{2 \sigma}{R},
$$
при $R = R_0$ и $q = q_0$ оно дает
$$
q_0 = p_\infty - p_v + \frac{2 \sigma}{R_0} \approx 113 ~\text{кПа}.
$$
С другой стороны при постоянной температуре
$$
q_0 R_0^3 = q R^3,
$$
поэтому
$$
p_\infty = p_v + q_0 \frac{R_0^3}{R^3} - \frac{2 \sigma}{R}.
$$
Критическому значению давления отвечает минимум $p_\infty$ как функции $R$. Этот минимум получается при
$$
R_c = R_0 \sqrt{\frac{3 q_0 R_0}{2 \sigma}} \approx 48~\text{мкм},
$$
соответствующее значение давления
$$
p_c= p_v - \frac{4}{3} \sqrt{\frac{2 \sigma^3}{3 q_0 R_0^3}} = p_v - 2 q_0 \left( \frac{R_0}{R_c}\right)^3 \approx 332~\text{Па}.
$$

B1  ^1.50 Пусть один сферический пузырек находится в воде, которая заполняет все пространство. Пузырек может менять размер (например из-за изменения внешнего давления $p_{\infty}$), при этом все время оставаясь сферическим.

Получите уравнение, которое связывает радиус пузырька $R(t)$ и его производные по времени $R'(t)$ и $R''(t)$, поверхностное натяжение $\sigma$, плотность воды $\rho$, давление вдали от пузырька $p_{\infty}$, и давление внутри пузырька $p$.

Затем разбейте давление $p$ внутри пузырька на два слагаемых, считая, что пузырек содержит пар (с парциальным давлением $p_v$) и воздух. Процесс для воздуха адиабатический, показатель адиабаты $\gamma$. Начальное давление воздуха $q_0$, начальный радиус пузырька $R_0$.

Считайте, что испарение, конденсация, или перенос воздуха между пузырьком и окружающей его водой не влияют на объем воды.

Пусть $v(r,t)$ — скорость элемента жидкости на расстоянии $r$ от центра пузырька в момент времени $t$, а $u(t) = v(R, t)$ — скорость на границе пузырька 

$$ u(t) = \dot{R}(t). $$

Тогда из условия несжимаемости получим 

$$ v(r,t) = \frac{R^2}{r^2} u(t).$$

 

Первый способ. Использование законов Ньютона

Запишем второй закон Ньютона для элемента жидкости. Для этого нам нужно найти его ускорение. Сначала вычислим производную по времени:
$$ \frac{\partial v}{\partial t} = \frac{\partial}{\partial t} \left( \frac{R^2}{r^2} u(t) \right) = \frac{2 R}{r^2} u^2 + \frac{R^2}{r^2} \dot{u}. $$
Скорость выбранного элемента жидкости меняется из-за двух причин. Во-первых распределение скоростей в пространстве меняется с течением времени. Во-вторых положение данного элемента жидкости в пространстве меняется с течением времени:
$$
\Delta v = v(r + \Delta r, t + \Delta t) - v(r, t),
$$
где изменение радиальной координаты $\Delta r = v \Delta t$. Тогда радиальное ускорение частицы жидкости
$$ a = \frac{\partial v}{\partial t} + v \frac{\partial v}{\partial r} = \frac{R^2}{r^2} \dot{u} + \frac{2R}{r^2} u^2 - \frac{2 R^4}{r^5} u^2. $$
Если $p = p(r)$ — давление на расстоянии $r$ (здесь мы явно не указываем возможную зависимость давления от времени), второй закон Ньютона имеет вид (штрих здесь — радиальная производная) $$ \rho a = - p', $$
или
$$ \frac{R^2}{r^2} \dot{u} +\left( \frac{2R}{r^2} - \frac{2 R^4}{r^5} \right)u^2 = - \frac{p'}{\rho}. $$
Проинтегрируем это уравнение от $r = R$ до $r = \infty$ и получим
$$ R \dot{u} + \frac{3}{2} u^2 = \frac{p(R) - p_\infty}{\rho}. $$
Поскольку давление внутри пузырька связано с давлением снаружи соотношением $$ p = p(R) + \frac{2\sigma}{R}, $$
мы получим $$ R \ddot{R} + \frac{3}{2} \dot{R}^2 + \frac{2\sigma}{\rho R} = \frac{p- p_\infty}{\rho}. $$ Наконец учтем, что давление в пузырьке складывается из давления пара $p_v$ и давления воздуха, а значит $$ p = p_v + q = p_v + q_0 \left( \frac{R_0}{R}\right)^{3 \gamma}, $$
откуда уравнение движения
$$
\rho R\ddot{R} + \frac{3}{2} \rho \dot{R}^2 + \frac{2\sigma}{ R} - q_0\frac{ R_0^{3 \gamma}}{R^{3 \gamma}} = p_v - p_\infty.
$$

Второй способ. Энергетический подход

Найдем кинетическую энергию движущейся жидкости. Масса жидкости на расстоянии от $r$ до $r + dr$ от центра пузырька равна
$$
dm = 4\pi r^2 \rho dr,
$$
откуда ее кинетическая энергия
$$
dE_k = \frac{dm }{2} v(r, t)^2 = 2 \pi \rho r^2 u^2 \frac{R^4}{r^4} dr .
$$
Тогда полная кинетическая энергия
$$
E_k = \int_R^{\infty} 2 \pi \rho u^2 R^4 \frac{dr}{r^2} = 2 \pi \rho R^3 u^2
$$
Также нужно учесть поверхностную энергию
$$
E_s = 4 \pi R^2 \sigma.
$$
Энергия жидкости и поверхности меняется за счет того, что давление воздуха внутри пузырька и жидкости на бесконечности совершают работу. За время $dt$ радиус пузырька меняется на величину $dR = u dt = \dot{R} dt$, поэтому газ внутри совершает работу
$$
dW_1 = 4\pi R^2 p dR = 4\pi R^2 p u dt.
$$
Для вычисления работы жидкости на бесконечности выберем сферу очень большого радиуса $R_1 \gg R$. Скорость элементов жидкости на этой поверхности
$$
u_1 = u \frac{R^2}{R_1^2},
$$
поэтому работа над жидкостью внутри этой сферы равна
$$
d W_2 = - 4 \pi R_1^2 p(R_1) u_1 dt = - 4\pi R^2 p(R_1) u dt.
$$
Когда радиус сферы стремится к бесконечности, мы можем заменить $p(R_1) = p_\infty$, и тогда радиус сферы исчезнет из выражения для работы. Тогда закон сохранения энергии имеет вид
$$
d(E_k + E_s) = dW_1 + dW_2.
$$
Вычисляя дифференциалы и сокращая $dt$, получим
$$
\frac{d}{dt} \left( 2 \pi \rho R^3 \dot{R}^2 + 4 \pi \sigma R^2\right) = 4\pi R^2 \dot{R}(p - p_\infty),
$$
откуда (после деления на $4\pi$ и сокращения общего множителя $R^2 \dot{R}$)
$$
\frac{3}{2} \rho \dot{R}^2 + \rho R \ddot{R} + \frac{2 \sigma}{R} = p- p_\infty.
$$
Подставляя выражения для $p$, получим то же уравнение

B2  ^1.00 Бак с водой с давлением $p_{\infty}^{-} = 101$ кПа содержит пузырек радиуса $R_0 = 10^{-5}$ м, изначально находящийся в состоянии равновесия. В некоторый момент времени давление мгновенно уменьшается до $p_{\infty} = 0$. Оцените предельное (асимптотическое) значение скорости роста пузырька $R'$, а также время, за которое скорость достигнет этого значения.

Используя то, что $\ddot{R} \to 0$ и $R \to \infty$, получим
$$
\dot{R}(\infty) = \sqrt{\frac{2 (p_v -p_\infty)}{3 \rho}} = \sqrt{\frac{2 p_v }{3 \rho}} \approx 1.24~\text{м}/\text{с}.
$$
Из уравнения движения найдем начальное ускорение
$$
\ddot{R}(0) = \frac{q_0 + p_v - 2\sigma/R_0}{\rho R_0} = \frac{p^-_\infty}{\rho R_0} \approx 10^7~\text{м}/\text{с}^2,
$$
и поэтому время установления скорости можно оценить как
$$
t \approx \frac{\dot{R}(\infty)}{\dot{R}(0)} \approx 0.1~\text{мкс}.
$$

B3  ^1.00 Бак с водой с давлением $p_{\infty}^{-} = 1.600$ кПа содержит пузырек радиуса $R_0 = 10^{-5}$ м, изначально находящийся в состоянии равновесия. В некоторый момент времени давление стало равно $p_{\infty} = 101$ кПа. Оцените минимальный радиус пузырька перед тем, как он начнет расширяться.

Умножим уравнение из B1 на $2 R^2 \dot{R}$, получим
$$
\rho \frac{d}{dt}\left[ R^3 \dot{R}^2\right]+ 4 \sigma R \dot{R} - 2 q_0 R_0^{3 \gamma} R^{2 - 3 \gamma}\dot{R} = 2 (p_v - p_\infty) R^2 \dot{R}.
$$
Проинтегрируем это уравнение от $R(0) = R_0$ и $\dot{R}(0) = 0$ до $R(t) = R$ и $\dot{R}(t)$, получим
$$
\rho R^3 \dot{R}^2 + 2 \sigma (R^2 - R_0^2) + \frac{2}{3 (\gamma -1)} q_0 R_0^{3 \gamma} \left( R^{3 - 3\gamma} - R_0^{3 - 3\gamma}\right) = \frac{2}{3} (p_v - p_\infty)(R^3 - R_0^3),
$$
или
$$
\rho \dot{R} ^2 = \frac{2 (p_v -p_\infty)}{\rho} - \frac{2 \sigma}{R} + \frac{2 R_0^3}{R^3} \left( \frac{\sigma}{R} + \frac{p_\infty - p_v}{3} + \frac{q_0}{3 (\gamma - 1)} - \frac{q_0 R_0^{3 \gamma -3}}{3 (\gamma -1) R^{3 \gamma -3}}\right).
$$
Это же соотношение является законом сохранения энергии, записанным в интегральной форме. Чтобы получить его непосредственно из закона сохранения энергии, подставим в выражение для работы из B1 явную зависимость давления от радиуса:
$$
dW = dW_1 + dW_2 = 4 \pi R^2 dR \left( p_v + q_0 \frac{R_0^{3 \gamma}}{R^{3 \gamma}} - p_\infty\right).
$$
Интегрируя от $R_0 $ до $R$, найдем полную работу
$$
W = \frac{4\pi}{3} (R^3 - R_0^3)(p- p_\infty) + \frac{4\pi q_0 R_0^{3 \gamma}}{3 - 3 \gamma} \left( R^{3 - 3 \gamma} - R_0^{3- 3 \gamma} \right).
$$
Она равна изменению энергии жидкости и поверхностной энергии
$$
\Delta (E_k + E_s) = 2\pi \rho R^3 \dot{R}^2 + 4 \pi \sigma (R^2 - R_0^2) = W.
$$
Подставляя выражения для работы и деля обе части на $2\pi R^3$, получаем прежнее выражение для $\rho \dot{R}^2$.

Когда радиус пузырька достигнет минимального значения, $\dot{R} = 0$. Если считать, что при этом $R \ll R_0$, то можно учитывать только наиболее быстро растущие слагаемые. Поскольку слагаемое с $1/R^3$ растет быстрее остальных, для оценки можно считать, что выражение в круглых скобках в формуле для $\rho \dot{R}^2$ должно быть равно нулю:
$$
\frac{\sigma}{R} + \frac{p_\infty - p_v}{3} + \frac{q_0}{3 (\gamma - 1)} - \frac{q_0 R_0^{3 \gamma -3}}{3 (\gamma -1) R^{3 \gamma -3}} =0,
$$
откуда
$$
\left( \frac{R_0}{R}\right)^{3 \gamma -3} = \frac{\gamma -1}{q_0} \left( p_\infty - p_v + \frac{3 \sigma}{R_0}\right) +1.
$$
Аналогично A2 найдем начальное значение давления воздуха внутри пузырька:
$$
q_0 = p_\infty^- - p_v +\frac{2 \sigma}{R_0} = 13.8~ кПа.
$$
Тогда численное значение минимального радиуса
$$
R \approx 2.88~ мкм.
$$
Точное решение уравнения $\dot{R}^2 = 0$ дает $R = 2.95 ~ мкм $.

B4  ^0.50 Если внутри пузырька находится только водяной пар, пузырек полностью схлопнется за конечное время. Определите показатель степени $\alpha$ в зависимости
\begin{equation*} R(t)\sim(T-t)^{\alpha}, \end{equation*}
где $T$ — время схлопывания.

При $R \ll R_0$ из уравнения движения следует (наиболее быстро растущее слагаемое в выражении для $\dot{R}^2$ ведет себя как $1/R^3$)
$$
R' \sim - R^{-3/2}.
$$
Подставим в это уравнение решение вида $R \sim (T- t)^\alpha$, получим
$$
(T- t)^{\alpha - 1} \sim (T- t)^{-3 \alpha/2},
$$
откуда
$$
\alpha - 1 = - \frac{3 \alpha}{2},
$$

Может показаться, что если использовать вместо закона сохранения непосредственно уравнение движения, получится другой показатель степени. Действительно, подставив в уравнение движения решение вида $R = A (T-t)^\alpha$, получим
$$
A (T-t)^\alpha A \alpha (\alpha -1) (T- t)^{\alpha - 2} + \frac{3}{2} A^2 \alpha^2 (T- t)^{2 \alpha} + \frac{2 \sigma}{\rho A} (T-t)^{-\alpha} = \frac{p_v - p_\infty}{\rho}.
$$
Тогда первые два слагаемых пропорциональны $(T- t)^{2\alpha-2}$, третье слагаемое порядка $(T- t)^{-\alpha}$, правая часть не зависит от времени, а слагаемое с $q_0$ по условию не учитываем. Тогда чтобы первые три слагаемых могли сократиться, нужно потребовать $2 \alpha - 2 = -\alpha$, $\alpha = 2/3$.

Однако это рассуждение работает только при условии, что коэффициент перед первыми двумя слагаемыми не равен нулю
$$
A^2\left( \alpha(\alpha -1) + \frac{3}{2} \alpha^2 \right) = A^2 \left( \frac{5}{2} \alpha^2 - \alpha\right).
$$
Однако он обращается в 0 как раз при правильном значении показателя степени $\alpha = 2/5$, так что никакого противоречия нет. Последующие слагаемые сократятся за счет поправок к лидирующему решению:
$$
R(t) = A(T-t)^{2/5} (1 + f (T- t) + \dots),
$$
при правильном выборе постоянной $f$.

B5  ^1.00 Используя уравнение, полученное в B3, найдите собственную частоту сферически-симметричных колебаний пузырька радиуса $R_0 = 0.1$ мм.

Для описания поведения пузырька введем безразмерную переменную $x$ согласно $R = R_0(1 + x)$, тогда уравнение движения
$$
\rho R_0^2 (1 + x)\ddot{x} + \frac{3}{2} R_0^2 \dot{x}^2 + \frac{2 \sigma}{R_0(1 + x)}- \frac{q_0}{(1 + x)^{3 \gamma}} = p_v - p_\infty.
$$
Считая колебания малыми, оставим только линейный по $x$ слагаемые. Тогда в первом слагаемом можно пренебречь $x$, вторым слагаемым можно пренебречь полностью, а оставшиеся разложить до первого порядка по $x$. Не зависящие от $x$ слагаемые сократятся в силу условия равновесия пузырька. Окончательно получим
$$
\rho R_0^2 \ddot{x} + \frac{2 \sigma}{R_0} (1 - x) - q_0 (1 - 3 \gamma x) =p_v - p_\infty, \quad \frac{2\sigma}{R_0} - q_0 = p_v - p_\infty,
$$
$$
\rho R_0^2 \ddot{x} + \left(3 \gamma q_0 - \frac{2 \sigma}{R_0} \right) x= 0.
$$
Тогда пузырек будет устойчив при условии $3 \gamma q_0 > 2 \sigma /R_0$, а частота колебаний (при вычислении считаем, что пузырек находится в равновесии при радиусе из условия и давлении $p_\infty = 101~ кПа$, откуда $q_0 \approx 100~ кПа$)

B6  ^1.00 Пусть пузырек, описанный в предыдущем пункте, находится в области, в которой есть стоячая звуковая волна. Давление в волне меняется вдоль оси $x$ как
\begin{equation*} p(x,t) = p_0 + A \sin\left(\frac{2\pi f}{c}(x+a)\right) \sin(2\pi ft) , \end{equation*}
где $f$ — частота, $c$ — скорость звука. Параметры $p_0$, $A$ и $a$ — постоянные, смысл которых можно понять из уравнения.

Найдите среднюю силу, действующую на пузырек. Он расположен в начале системы координат $xyz$, его размер много меньше длины волны звука.

Будем использовать то же линеаризованное уравнение колебаний пузырька, но теперь учтем, что давление на бесконечности меняется по закону из условия
$$
\rho R_0^2 \ddot{x} + \left(3 \gamma q_0 - \frac{2 \sigma}{R_0} \right) x= A \sin\left(\frac{2\pi f}{c}a\right) \sin(2\pi ft).
$$
Установившееся решение имеет вид $x = B \sin (2\pi f t)$, амплитуду решения можно найти, подставив его в уравнение. Для упрощения записи ответов выразим коэффициент перед $x$ через $f_0^2$:
$$
\rho R_0^2 4\pi^2 (f_0^2 - f^2) B \sin (2\pi f t) = A \sin\left(\frac{2\pi f}{c}a\right) \sin(2\pi ft),
$$
откуда решение имеет вид
$$
x(t) = \frac{A \sin\left(\frac{2\pi f} {c}a\right)}{4\pi^2 \rho R_0^2 (f_0^2 -f^2)} \sin (2\pi f t).
$$
Давление меняется с координатой, поэтому на пузырек действует сила, аналогичная силе Архимеда
$$
F_x = - \rho g_x V,
$$
где $g_x$ — эффективное ускорение свободного падения, которое можно найти, зная градиент давления:
$$
\rho g_x = \frac{\partial p}{\partial x}.
$$
Тогда среднее по времени значение силы
$$
F = -\left\langle V \frac{\partial p}{\partial x}\right\rangle.
$$
Объем пузырька
$$
V = \frac{4 \pi }{3 } R^3 = \frac{4 \pi }{3 } R^3_0 (1 + x)^3 \approx \frac{4 \pi }{3 } R^3_0(1 + 3x),
$$
постоянное слагаемое сократится при усреднении, тогда получим
$$
F = - 4\pi R_0^3 \left\langle x \frac{\partial p}{\partial x}\right\rangle
= - 4\pi R_0^3 \frac{A \sin\left(\frac{2\pi f} {c}a\right)}{4\pi^2 \rho R_0^2 (f_0^2 -f^2)}
\left\langle\sin (2 \pi ft) \frac{2 \pi f}{c} A \cos\left( \frac{2\pi f}{c} f\right) \sin(2\pi ft)\right\rangle.
$$
Используя среднее от квадрата синуса $\langle \sin^2 (2\pi ft) = 1/2$ и формулу для синуса двойного угла, получим окончательно

C1  ^2.00 Пусть пузырек радиуса $R_0 = 10^{-5}$ м, содержащий воздух и пар, находится в растворе воздуха в воде, в котором растворенный воздух находится в равновесии с воздухом при атмосферном давлении.

Парциальное давление воздуха в пузырьке $q = 1.70\cdot 10^5$ Па, давлением пара можно пренебречь. Оцените время, за которое пузырек полностью растворится в воде.

Значения величин $p_{\infty}$, $\kappa$, $\delta$ и $\sigma$ возьмите в таблице 1. Считайте, что область вокруг пузырька, в которой происходит диффузия воздуха, мгновенно становится много больше самого пузырька.

Концентрация растворенного воздуха на большом расстоянии до пузырька
$$
u_i = H p_\infty,
$$
а концентрация вблизи пузырька
$$
u = H q > u_i,
$$
поэтому возникнет диффузионный поток растворенного воздуха, направленный от пузырька. Из-за этого масса воздуха внутри пузырька будет убывать, и со временем пузырек полностью растворится.
Оценим поток воздуха из пузырька. Для оценки примем, что концентрация растворенного воздуха существенно изменяется на расстоянии порядка радиуса пузырька, тогда полный поток
$$
J = 4 \pi R^2 \kappa \frac{u - u_i}{R} = 4\pi R \kappa H(q - p_\infty).
$$
Поскольку давлением водяного пара можно пренебречь, давление воздуха в пузырьке
$$
q = p_\infty + \frac{2 \sigma}{R}.
$$
Тогда окончательное выражение для потока массы из пузырька
$$
J = 4 \pi R \kappa H \frac{2\sigma}{R} = 8 \pi \kappa H \sigma.
$$
Видим, что это выражение не зависит от радиуса, поэтому для оценки времени можно просто разделить полную массу воздуха в пузырьке на поток. Эта масса равна
$$
m = \frac{4\pi}{3} R^3_0 \frac{\delta}{p_\infty} \left( p_\infty + \frac{2 \sigma}{R_0}\right).
$$
Здесь $\delta$ — плотность воздуха при атмосферном давлении $p_\infty$.
Тогда время жизни пузырька
$$
t \approx \frac{m}{J} = \frac{\frac{4\pi}{3} R_0^3 \delta \left( 1 + \frac{2 \sigma}{p_\infty R_0}\right)}{8 \pi \kappa H \sigma} = \frac{R_0^3 \delta}{6 \kappa \sigma H} \left( 1 + \frac{2 \sigma}{p_\infty R_0} \right)
$$

В основной части решения мы использовали оценку для потока воздуха из пузырька
$$
J = 4 \pi R^2 \kappa \frac{u - u_i}{R}.
$$
Из качественных соображений невозможно получить коэффициент в формуле. Рассмотрев решение уравнения диффузии покажем, что коэффициент действительно выбран правильно (на олимпиаде такое вычисление в действительности требовалось от участников).
Рассмотрим сферу радиуса $r$ и толщины $dr$. Скорость изменения массы воздуха в этой сфере можно выразить через производную концентрации:
$$
\frac{dm}{dt} = 4\pi r^2 dr \frac{\partial u}{\partial t}.
$$
С другой стороны, ее можно выразить как разность втекающих и вытекающих потоков
$$
\frac{dm}{dt} = 4\pi (r + dr)^2 J(r + dr) - 4\pi r^2 J(r) = 4\pi (r + dr)^2 \kappa\frac{\partial u}{\partial r} (r + dr) - 4\pi r^2 \kappa \frac{\partial u}{\partial r} (r).
$$
Используя соотношение
$$
\frac{\partial u}{\partial r} (d + dr) = \frac{\partial u}{\partial r} (r) + \frac{\partial ^2 u}{\partial r^2}(r) dr,
$$
получим
$$
\frac{dm}{dt} = 4\pi r^2 \kappa dr \frac{\partial^2 u}{\partial r^2} + 8 \pi r \kappa dr \frac{\partial u} {\partial r}.
$$
Объединив эти два уравнения, получим
$$
\frac{\partial u}{\partial t} = \kappa \frac{\partial^2 u}{\partial r^2} + \frac{2 \kappa}{r} \frac{\partial u} {\partial r}.
$$
В начальный момент времени во всем объеме воды концентрация растворенного воздуха одинакова и равна $u = u_i$. Во все моменты времени концентрация воздуха в непосредственной окрестности пузырька равна $H q$:
$$
\begin{cases}
u(r, 0) = u_i \quad \text{ при } r >R,\\
u(R, t) = Hq, \quad \text{ при } t >0.
\end{cases}
$$

Введем новую переменную $v = r(u - q H)$, и новый параметр времени $\tau = \kappa t$. Тогда уравнение диффузии перейдет в
$$
\frac{\partial v}{\partial \tau} = \frac{\partial ^2 v}{\partial r^2},
$$
с граничными условиями
$$
\begin{cases}
v(r, 0) = r(u_i -q H) \quad \text{ при } r >R,\\
v(R, t) = 0 \quad \text{ при } \tau >0.
\end{cases}
$$
Также введем переменную $\xi = r - R$ и функцию $w(\xi, \tau) = v(R + \xi, \tau)$, тогда
$$
\frac{\partial w}{\partial \tau} = \frac{\partial ^2 w}{\partial \xi^2},
$$
с граничными условиями
$$
\begin{cases}
w(\xi, 0) = (R + \xi)(u_i -q H) \quad \text{ при } \xi > 0,\\
w(0, t) = 0 \quad \text{ при } \tau >0.
\end{cases}
$$
Решение этого уравнения имеет вид
$$
w(\xi, \tau) = \frac{u_i - qH}{\sqrt{4\pi \tau}} \int_0^{\infty} \left(e^{- (\xi - \eta)^2/(4 \tau)} - e^{- (\xi + \eta)^2/(4 \tau)}\right) (\eta + R) d\eta.
$$
Поскольку
$$
u(r,t) = q H + \frac{v(r, \kappa t)}{r} = qH + \frac{w(r - R, \kappa t)}{r},
$$
производная имеет вид
$$
\frac{\partial u}{\partial r} = \frac{1}{r} \frac{\partial w}{\partial \xi} - \frac{w}{r^2},
$$
откуда
$$
\left. \frac{\partial u}{\partial r}\right|_{r = R} = \frac{1}{R} \left. \frac{\partial w}{\partial \xi} \right|_{\xi = 0} = (u_i - qH) \left( \frac{1}{R} + \frac{1}{\sqrt{\pi \kappa t}}\right).
$$
Здесь знаменатель второго слагаемого порядка характерного размера диффузионной области, в которой существенно меняется концентрация. Мы считаем, что размер этой области много больше размера пузырька, поэтому вторым слагаемым можно пренебречь. С учетом этого поток воздуха через поверхность пузырька
$$
J = - 4\pi R^2 \kappa \left. \frac{\partial u}{\partial r}\right|_{r = R} = 4\pi R^2 \kappa \frac{u - u_i}{R}.
$$
Это и есть выражение, которое мы использовали в основной части решения.

C2  ^0.50

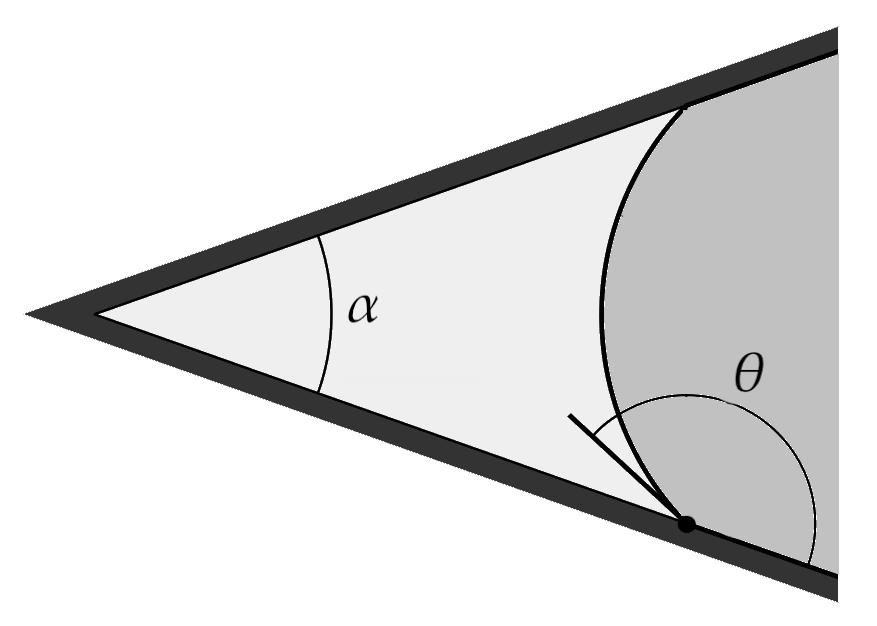
Условия равновесия имеют вид
$$
p_v + q = p_\infty \pm \frac{2\sigma}{R}, \quad u = Hq.
$$
Выбор знака зависит от направления выпуклости границы. Пусть начальное давление воздуха в пузырьке равно $q$. При больших значениях давления воздуха в пузырьке $q$, это давление будет убывать, а пузырек будет уменьшаться. В некоторый момент система придет в равновесие. Объем воздуха не исчезнет полностью, если поверхность воды выпуклая (и давление внутри может быть меньше давления на бесконечности, так что диффузия остановится):