
Механика контактного взаимодействия — классическая теория, описывающая взаимодействие тел при их динамическом контакте. Прежде всего, данная теория связана с именем Г. Герца, который первым получил значимые результаты в этой области. Вывод теории достаточно сложен, однако финальные уравнения в некоторых случаях решаются аналитически. Теория Герца следует из решений уравнений теории упругости с учётом следующих приближений:
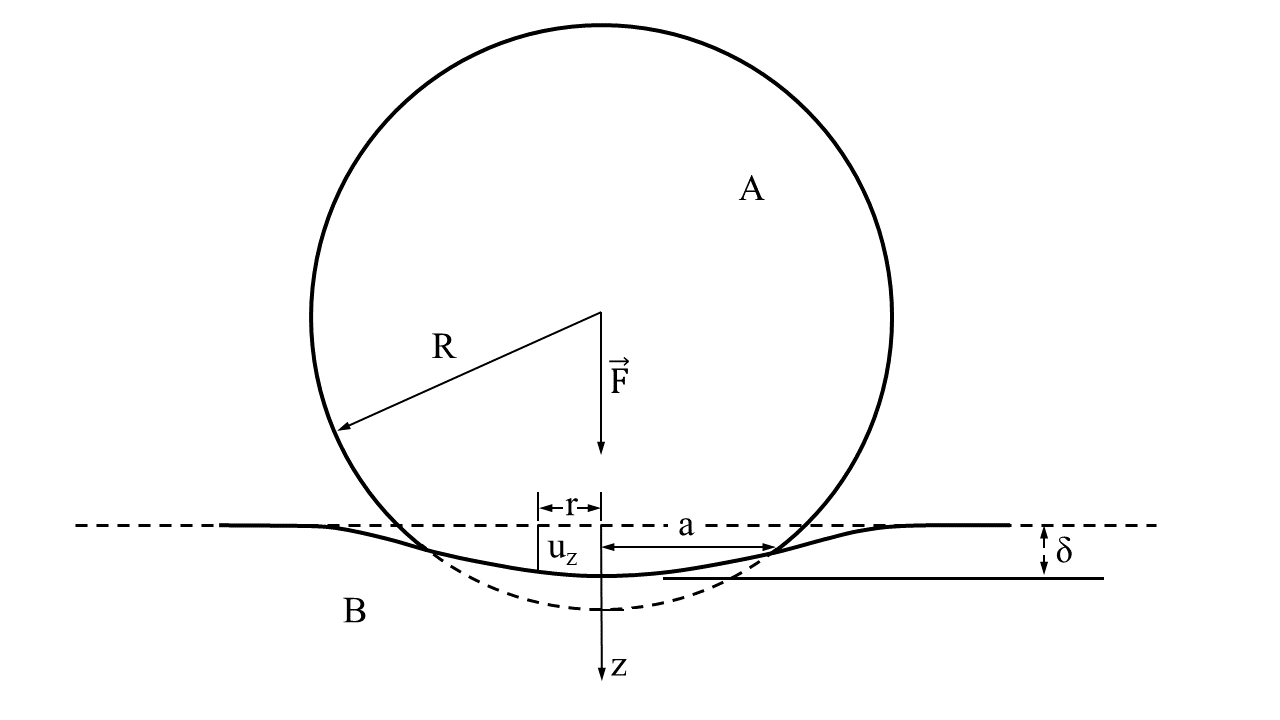
Если на поверхность действуют только вертикальные силы, её вертикальное смещение может быть описано следующим выражением:
$$u_z (x,y)=\frac{2\pi}{E'}\int_{}\int{\frac{p(x',y')}{\sqrt{(x-x')^2+(y-y')^{2}}}dx'}{dy'}$$
Здесь $u_z$ — вертикальное смещение, $E'$ — эффективный модуль Юнга ($\frac{1}{E'} = \frac{(1-v_1^2)}{E_1} + \frac{(1-v_2^2)}{E_2}$, где $v_1$, $E_1$, $v_2$, $E_2$ — коэффициенты Пуассона и модули Юнга контактирующих тел соответственно, они являются постоянными для выданных шариков, их значения будут указаны в пункте E.1), $p(x,y)$ — контактное давление.
Решение Герца получено для случая параболического профиля давлений (в общем случае уравнение не решается аналитически). В параболическом приближении хорошо описываются контакты сферических, эллиптических и цилиндрических тел.
$$p(r)=p_{0}\left(1-\frac{r^{2}}{a^{2}}\right)^{1/2}$$
где $r$ — расстояние до произвольной точки плоскости. $a$ называется контактным радиусом Герца, $p_0$ — максимальным давлением Герца. Подстановкой этого уравнения в уравнение $(1)$ получается выражение для смещения Герца:
$$u_{z}=\frac{\pi p_{0}}{4E'a}(2a^{2}-r^{2}), r\le a$$
Эта задача состоит из двух частей:

В этой части задачи вам нужно найти зависимость максимальной скорости маятника от амплитуды его колебаний во всём диапазоне углов, доступных для измерения. Для проведения измерений вам потребуется менять параметры маятника.
На каждом подвесе расположены две ручки (два гитарных колка). Они используются для регулировки положения шарика вверх/вниз (по оси $z$) и вперёд/назад (по оси $y$). Для регулировки влево/вправо (по оси $x$) используйте подвижную каретку, закреплённую двумя винтами (Рис. 3).
В этой части используйте только один маятник. Второй шарик уберите наверх. Убедитесь, что его нити не препятствуют движению исследуемого маятника.
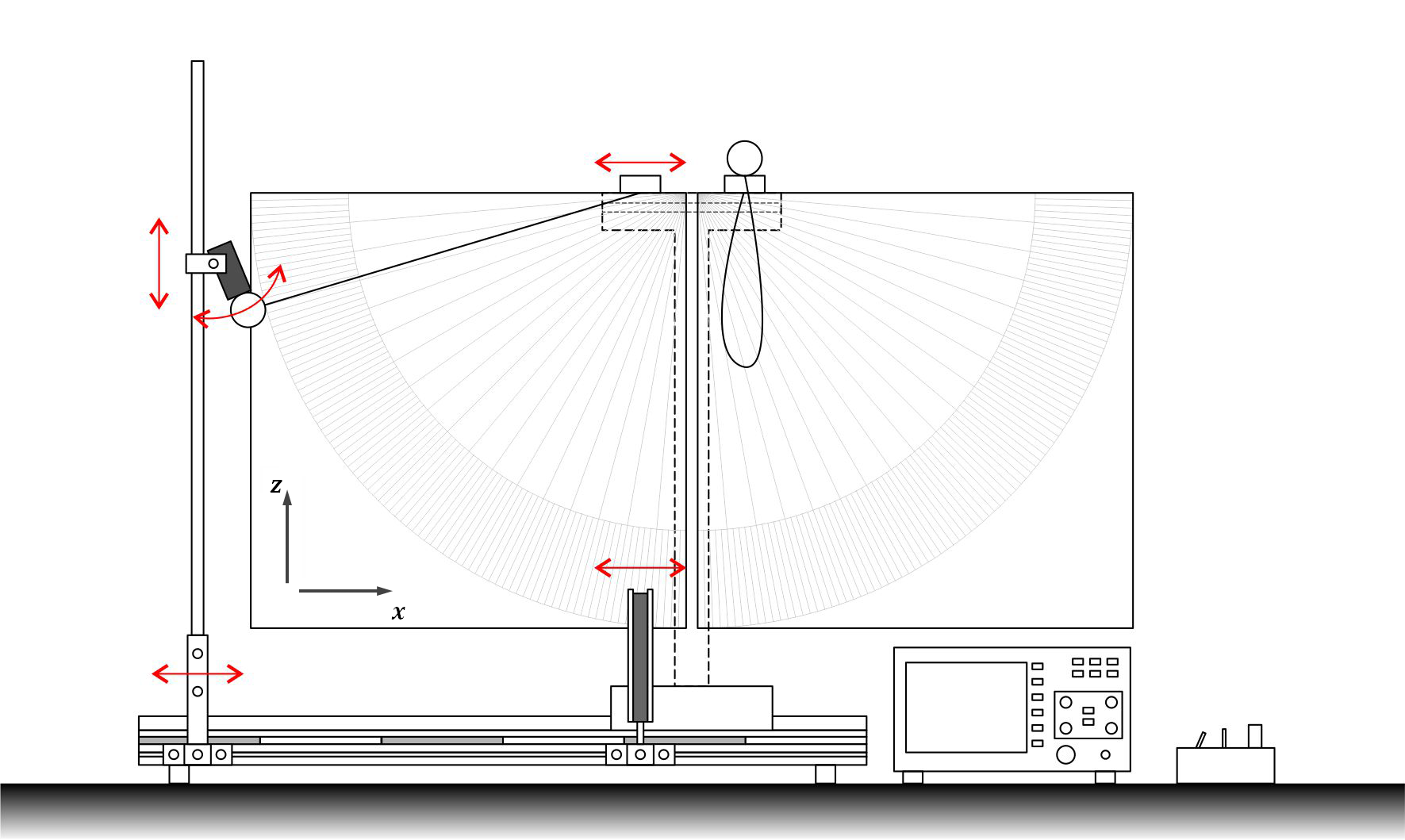
A1 1.20 Найдите угловой коэффициент графика $\Delta t^{-1}$ от $\sin \frac{\varphi_0}{2}$, где $\varphi_0$ — угловая амплитуда колебаний маятника, $\Delta t$ — время пролёта шарика через фотодатчик.
Примечание 1. Чтобы измерить период с помощью осциллографа достаточно точно, вы можете ознакомится с инструкцией по работе с осциллографом, приведённой в регламенте, а также выполнить упражнения, расположенные там же. Обратите внимание на модель вашего осциллографа.
Для экономии времени можно выполнить пункт B.1 вместе с этим пунктом. Упругость нити и намагниченность шарика могут повлиять в начальный момент на его движение. Поэтому не следует проводить измерения при первом пролёте шарика через фотодатчик.
Зависимость периода колебаний маятника от угловой амплитуды задаётся следующим рядом:
$$T=T_0\left(1+\alpha\cdot\sin^2\frac{\varphi_0}2+\beta\cdot\sin^4\frac{\varphi_0}2+\ldots\right)$$
Здесь $T_0$ — период малых колебаний маятника, $\alpha$ и $\beta$ — некоторые постоянные, а $\varphi_0$ — угловая амплитуда.
B1 1.60 Сняв зависимость периода колебаний от угловой амплитуды, постройте линеаризованные графики зависимости $T=f(\varphi_0)$. Учтите, что для разных диапазонов угла могут потребоваться разные линеаризации.
Определите по этим графикам величины $T_0$, $\alpha$ и $\beta$.
Примечание 2. Чтобы измерить период с помощью осциллографа достаточно точно, вы можете ознакомится с инструкцией по работе с осциллографом, приведённой в регламенте, а также выполнить упражнения, расположенные там же. Обратите внимание на модель вашего осциллографа.
Начальные положения шариков и многие другие параметры установки заметно влияют на длительность столкновений, а также на положения точек контакта шариков. Поэтому при выполнении этой части задачи будьте предельно аккуратны при юстировке положения шариков.
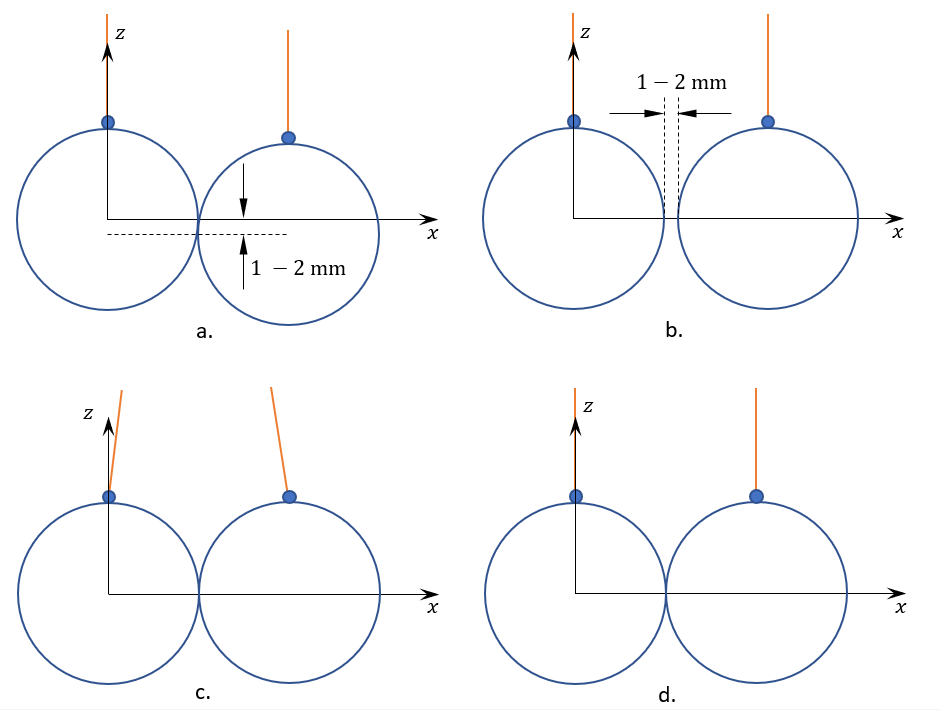
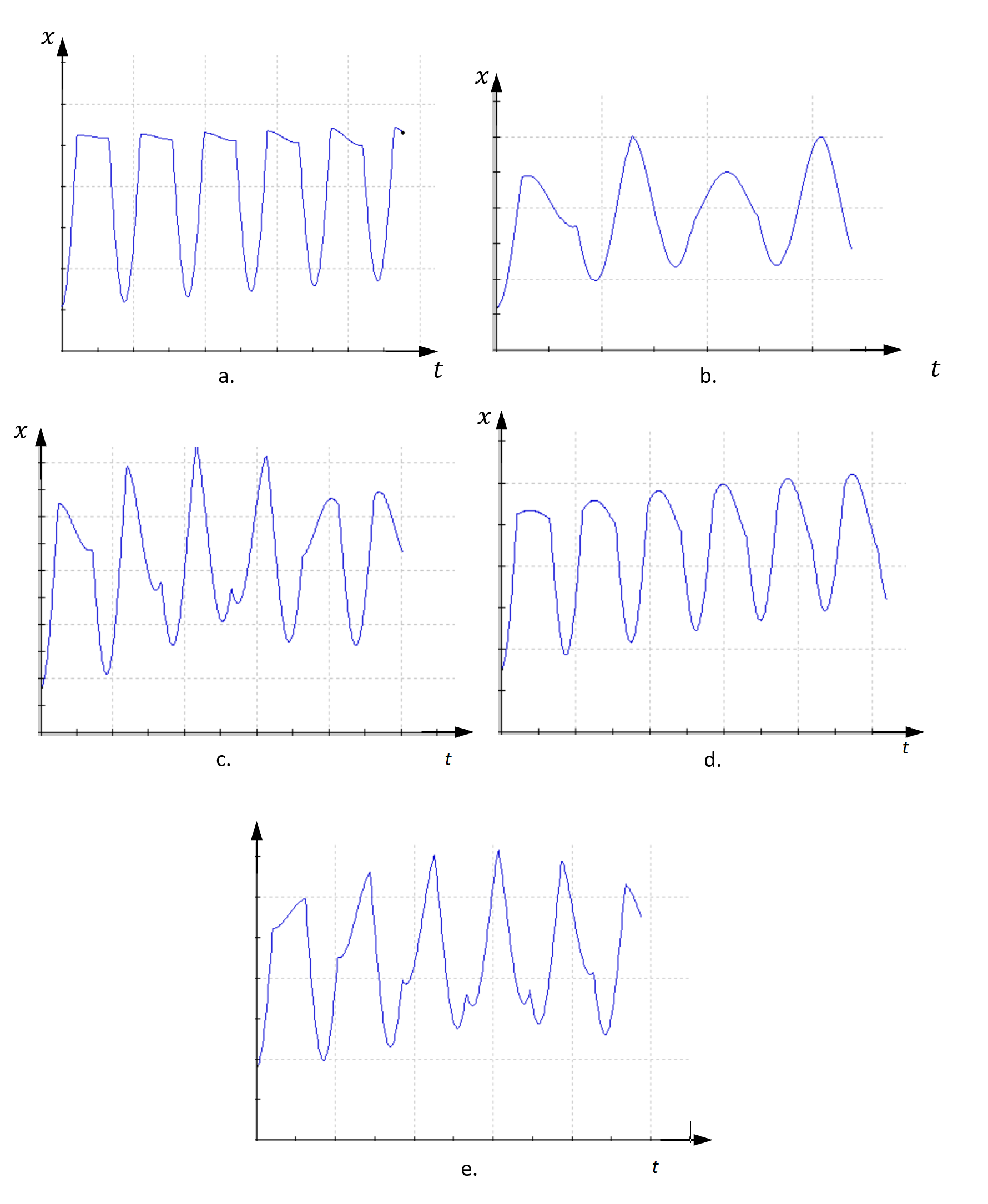
В этой части нужно пронаблюдать, как положение точки контакта шариков влияет на их поведение при соударениях. Случаи, которые необходимо рассмотреть, описаны в пунктах C.1—C.4 (положения шариков в состоянии покоя показаны соответственно на Рис. 4). На Рис. 5 приведены графики зависимости координаты $x$ одного из шариков от времени. В пунктах этой части задачи каждому положению на Рис. 4. нужно сопоставить один из графиков на Рис. 5.
C1
0.20
Когда оба шарика находятся в покое и равновесии, примем положение центра первого шарика за начало координат. Тогда положения шариков можно описать так: расстояние между центрами двух шариков по оси $x$ равно $d_x=2R$, расстояние по оси $y$ равно $d_y=0$, расстояние по оси $z$ равно $d_z \approx 1-2~$мм, а нити, на которых подвешены шарики, практически параллельны (см. рисунок 4a).
Отклоните шарик 1 на угол $25^\circ-35^\circ$ и отпустите без начальной скорости (шарик 2 покоится).
Запишите букву соответствующего графика в лист ответов.
C2
0.20
Условия эксперимента: $d_x-2R\approx1~$мм, $d_y=0$, $d_z=0$, нити параллельны. Этого можно добиться, раздвинув точки подвеса шариков на $1~$мм (см. рисунок 4b).
Отклоните шарик 1 на угол $25^\circ-35^\circ$ и отпустите без начальной скорости (шарик 2 покоится).
Запишите букву соответствующего графика в лист ответов.
C3
0.20
Условия эксперимента: $d_x\approx2R$, $d_y=0$, $d_z=0$, точки подвеса шариков соприкасаются. Нити в этом случае не будут параллельны (см. рисунок 4c).
Отклоните шарик 1 на угол $25^\circ-35^\circ$ и отпустите без начальной скорости (шарик 2 покоится).
Запишите букву соответствующего графика в лист ответов.
При соударении шарики будут некоторое время соприкасаться, пока снова не разлетятся. В этой части задачи исследуется зависимость времени соударения ($\tau$) от различных параметров шариков. Для получения зависимости вам нужно будет исследовать параметры соударений шариков одинакового или разного размеров.
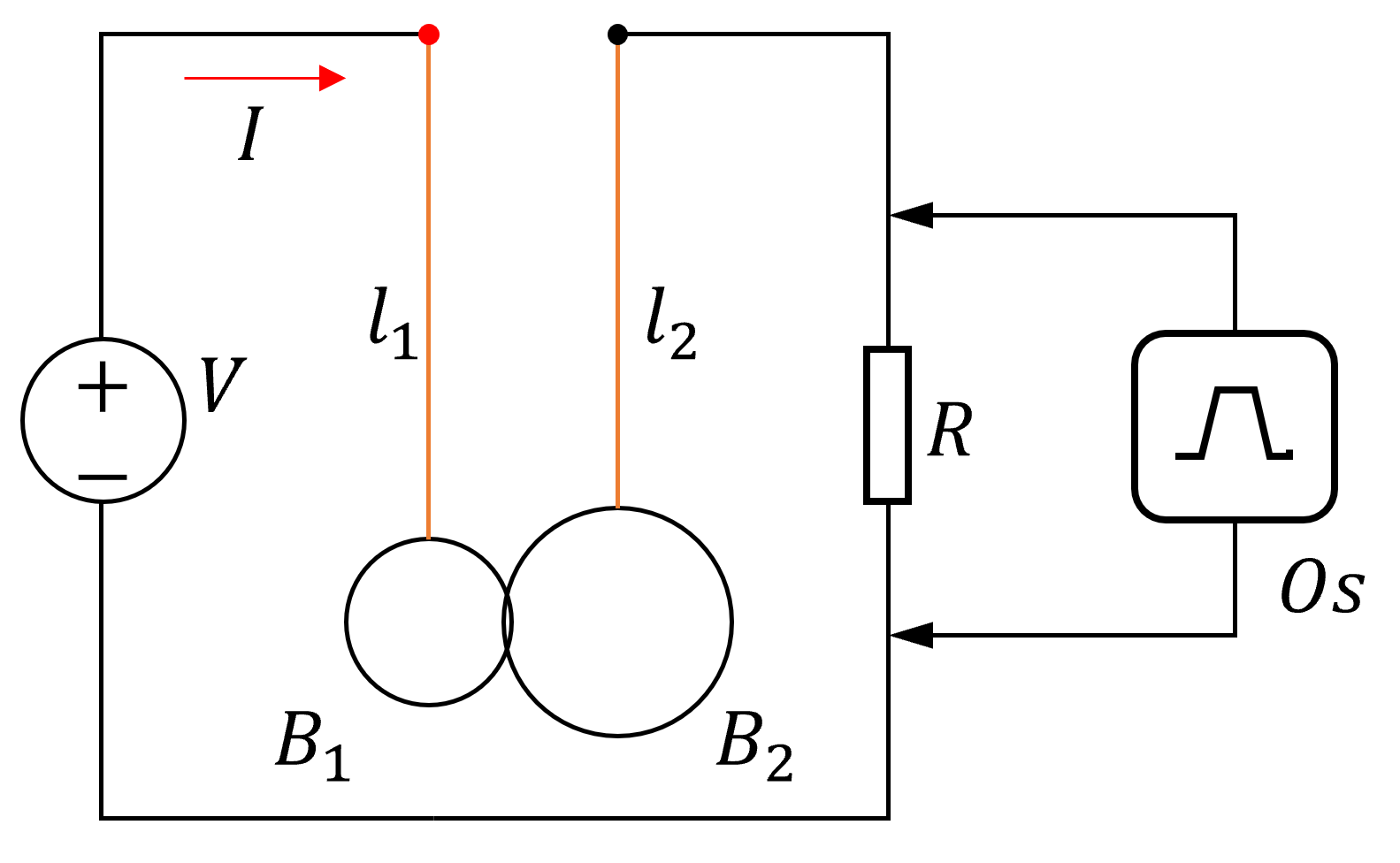
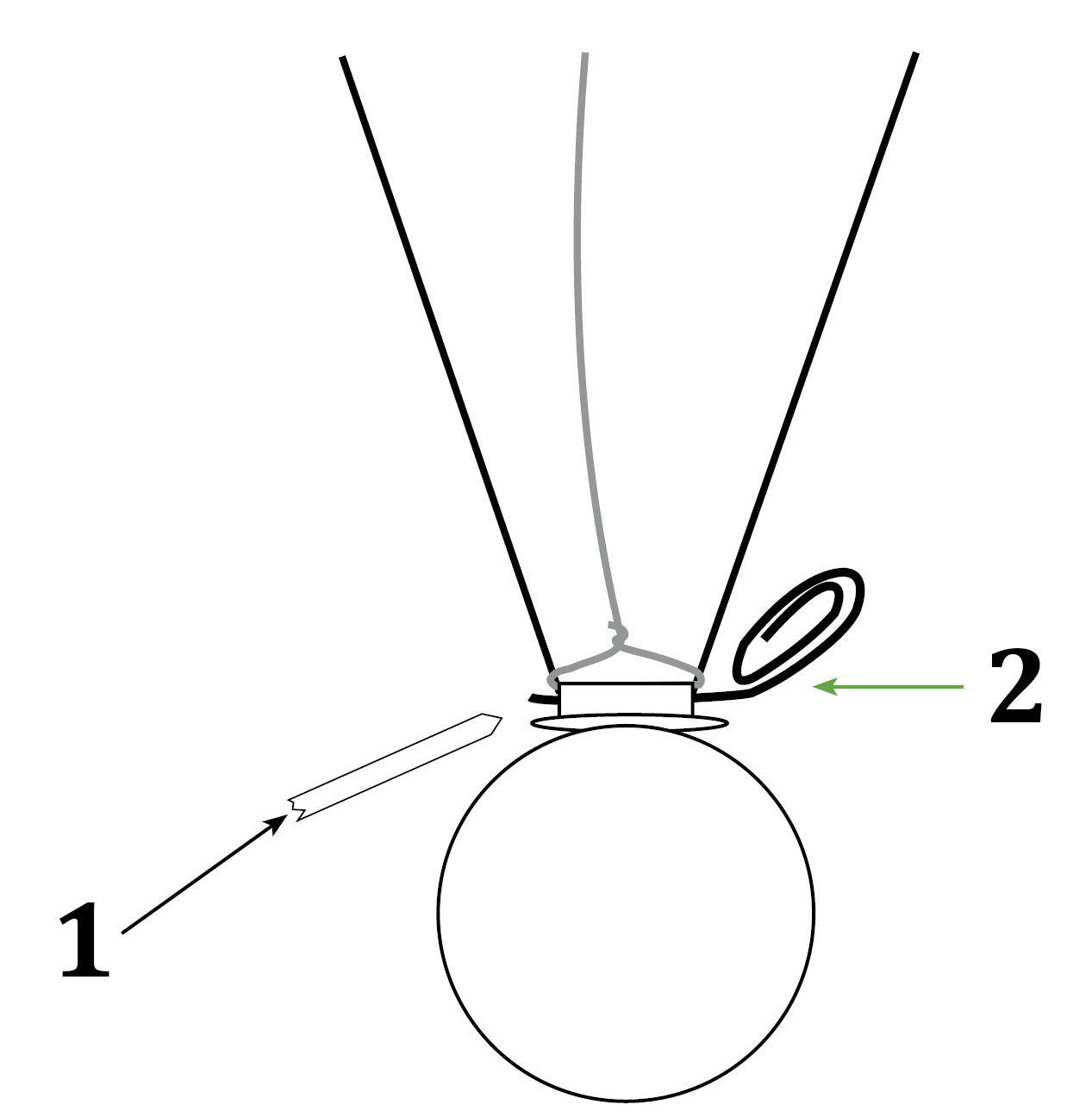
Для измерения времени соударения используется электрическая цепь, показанная на рисунке 6. К шарикам прикреплены дополнительные тонкие металлические провода, нейлоновые нити используются только в качестве подвеса маятника. Обеспечьте надёжный контакт проводов с шариками. Для этого используйте выданные зубочистки. С их помощью можно закрепить провода и нейлоновые нити в креплении шарика. Вставляйте зубочистку только с одной стороны крепления! Для замены проводов необходимо достать зубочистку, для этого вам выдана скрепка (Рис. 7).
D1
0.40
Время соударения шариков $\tau$ задаётся выражением:
$\tau\:=\:_{ }A\cdot x_1^{e_1} \cdot x_2^{e_2}\cdot... \:\cdot x_n^{e_n}$,
где $A$ — безразмерная постоянная, а $x_1$, $x_2$, $\ldots$, $x_n$ — параметры, влияющие на соударение.
Каким физическим величинам соответствуют эти параметры? Показатели $e_1$, $e_2$, $\ldots$, $e_n$ будут определены в пунктах D.2 и D.3.
Используя выражение для максимальной скорости, полученное в пункте A.2, и экспериментальные данные, полученные в пункте D.2, найдите следующие параметры для нескольких значений начальных углов.
($\nu=\nu_1=\nu_2=0.3$, $E=E_1=E_2=200~$ГПа, массы шариков $m_1=131.48~$г, $m_2=67.55~$г, диаметры шариков $d_1=31.75~$мм, $d_2=25.42~$мм.)