Градиентная оптика~— раздел оптики, изучающий оптические свойства материалов, показатель преломления которых изменяется в зависимости от координат.

Примером градиентной оптики является мираж лужи на дороге в жаркий день. В действительности лужа это изображение неба на дороге, так как лучи света преломляются (изгибаются) от их нормальной прямолинейной траектории. Это происходит из-за изменения показателя преломления между тёплым и менее плотным воздухом у поверхности дороги и более плотным и холодным воздухом над ней. Другой известный пример~— это оптоволокно, в котором свет распространяется по гармоническому закону в завимисимости от продольной координаты.

Предлагаемая вам экспериментальная задача состоит из трех независимых частей, у которых, тем не менее, есть общее оборудование. В каждой из частей вам нужно будет создавать градиенты показателя преломления в веществе и исследовать их.

Оборудование

1. Блок питания
2. Экран
3. 4 держателя
4. Рулетка
5. «Сэндвич»
6. Красный лазер (точка)
7. Отвертка (для регулировки крепежа держателей)
8. Линейка
9. Лезвие ножа
10. Шприцы с желе
11. Клейкая масса
12. Прозрачные пластины
13. Крышка, на которой резать желе
14. Фонарик
15. Сосуд с водой
16. Пара зеркал
17. Пробирки с растворами соли
18. Пробирка с дистилированной водой
19. Красный лазер (линия)
20. Пипетка
21. Секундомер
22. Кювета
23. Штатив для кюветы

Часть А. Температурный градиент в оргстекле (5 баллов)

\emph{Оборудование, используемое в этой части:} блок питания (1), экран (2), держатель лазера (3), рулетка (4), «сэндвич» (5), лазер (6), отвертка (7), линейка (8), пара зеркал (16).

Коэффициент преломления материала зависит от температуры следующим образом:
$$
n(T)=n_0 + \alpha (T-T_0),
$$
где будем считать $T_0$~— комнатной температурой, $n_0$~— показателем преломления при комнатной температуре, а $\alpha$~— температурным коэффициентом показателя преломления.

Оргстекло (плексиглас) обладает сравнительно большим температурным коэффициентом показателя преломления, поэтому на имеющемся оборудовании можно наблюдать эффекты, связанные с измерением показателя преломления вдоль одной из осей.

Нагревая оргстекло с двух сторон, можно создать градиент температуры внутри оргстекла. В установившемся режиме можно с хорошей точностью считать, что температура линейно изменяется вдоль оси $y$. Ход луча показан на рисунке ниже. При решении задачи используйте обозначения, указанные на рисунке.

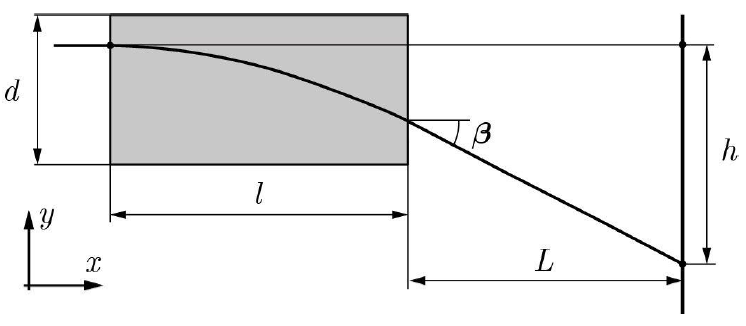
Оргстекло для проведения эксперимента помещено между двумя парами элементов Пельтье. Элемент Пельтье создает разность температур между двумя своими плоскими поверхностями. В собранном «сэндвиче» при правильном подключении источника напряжения, сторона с радиатором охлаждает поверхность оргстекла, к которой она приклеена. Противоположная сторона (без радиатора) соответственно нагревает поверхность оргстекла.

При нагревании оргстекла выше $70~{}^\circ\mathrm{C}$ происходят необратимые изменения в его структуре. Поэтому в провода, идущие к элементам Пельтье, встроены предохранители номиналом в $0.75~\mathrm{А}$. Не превышайте ток в $0.75~\mathrm{А}$ через элементы Пельтье. При параллельном соединении верхних и нижних пар элементов Пельтье показания источника не должны превышать $1.5~\mathrm{А}$ соответственно.

\emph{Если вы сожжете предохранитель, ваши баллы за этот пункт аннулируются.}

Для собранных «сэндвичей» ниже приведен график зависимости разности температур между поверхностями оргстекла от силы тока, текущего через каждую пару элементов Пельтье. Характерное время установления стационарного распределения температуры для «сэндвичей» составляет около 3 минут.

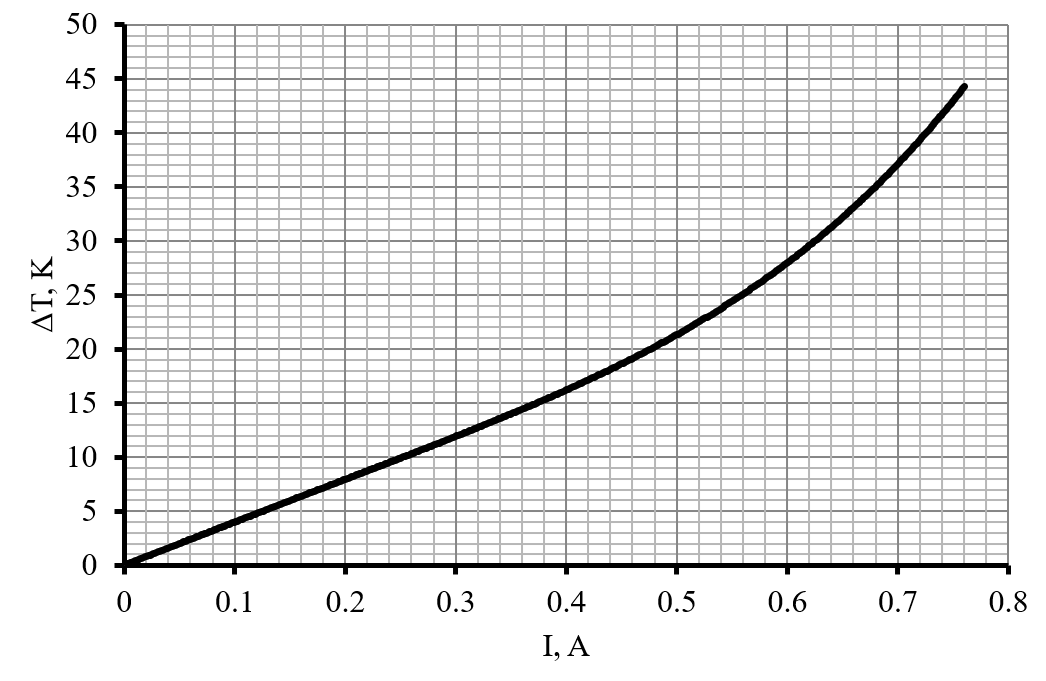
Обратите внимание на боковую поверхность оргстекла. Короткие стороны отполированы значительно лучше, чем длинные. Поэтому используйте короткие стороны для изучения эффекта. При необходимости вы можете использовать пару зеркал для увеличения расстояний, на которых вы наблюдаете эффект.

A1  ^0.50 Нарисуйте схему установки для определения градиента показателя преломления, соответствующую схеме выше. Укажите на ней все необходимые измеряемые величины.

A2  ^2.00 Подключите две пары элементов Пельтье параллельно к источнику напряжения. Снимите зависимость вертикального смещения~$h$ луча лазера от тока~$I$, текущего через источник.

Для обработки данных вам может понадобиться уравнение траектории луча в объеме оргстекла. Полагая, что показатель преломления зависит от $y$ следующим образом $n(y)=n(0)-ky$, координаты траектории связаны так:
$$
x=\cfrac{n(0)}{k}\ln\left(1-\cfrac{ky}{n(0)}+\sqrt{\left(1-\cfrac{ky}{n(0)}\right)^2-1}\right).
$$
Направление осей приведено на рисунке.

A3  ^1.00 Постройте график зависимости вертикального смещения луча от разности температур между поверхностями оргстекла $h(\Delta T)$. Определите параметры фитирующей линии.

A4  ^1.50 Приведите формулу, связывающую определенные в пункте A4 параметры и температурный коэффициент показателя преломления $\alpha$ оргстекла. Найдите численное значение $\alpha$ и оцените его погрешность.

Часть B. Диффузия соли (10 баллов)

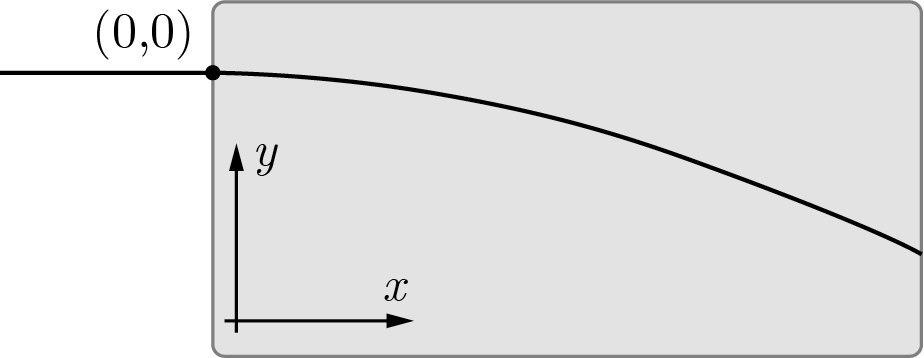
В этой части задачи будет исследоваться градиент, образующийся на границе двух растворов~— концентрированного раствора соли и дистиллированной воды. Показатель преломления жидкости зависит от концентрации соли. Таким образом, можно изучить процесс диффузии оптическим методом по отклонению лазерного луча от прямолинейного распространения.

В этой части задачи не требуется оценка погрешностей.

\emph{Оборудование, используемое в этой части задачи:} экран (2), держатель лазера (3), рулетка (4), отвертка (7), линейка (8), пробирки с растворами соли (17), пробирка с водой (18), красный лазер линия (19), пипетка (20), секундомер (21), кювета (22), штатив для кюветы (23), ведро (24).

Схема установки для этой части задачи приведена на рисунке.

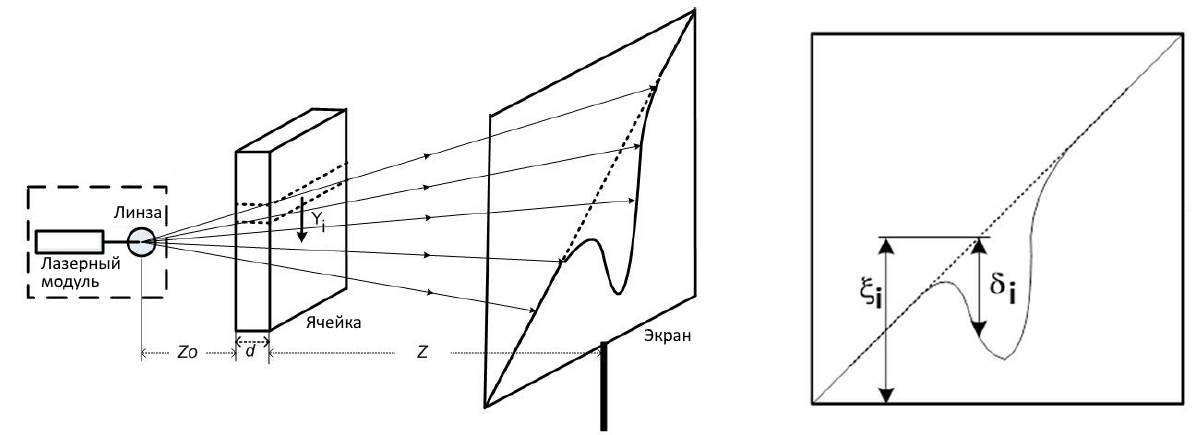
Чтобы определить функцию зависимости градиента показателя преломления от координаты (по вертикали), нужно получить соответствие между координатой на экране $\xi_i$ и координатой $Y_i$ в кювете, а также нужно получить соответстве между вертикальным отклонением $\delta$ и локальным градиентом показателя преломления $dn/dY$. Из геометрии установки можно получить $Y_i=\cfrac{\xi_i Z_0}{Z_0+d+Z}$. Также можно показать, что справедливо $\left(\cfrac{dn}{dY}\right)_i=\cfrac{\delta_i}{Zd}$.

Соберите установку, согласно схеме, приведенной выше. В этой части задачи нужно использовать красный лазер, который дает изображение в виде прямой линии. В зависимости от расстояний, на которых вы работаете, может потребоваться фокусировка луча лазера. Это делается вращением передней линзы. Добейтесь минимальной толщины линии для своей установки.

Поместите пустую кювету на пути луча лазера. На экране вы должны получить изображение наклонной линии. Залейте в кювету раствор соли. Налейте его до уровня первого разделителя. Наливайте раствор соли в широкую часть кюветы аккуратно, по боковой стенке. Затем налейте дистиллированную воду. Наливайте воду по каплям в узкую часть кюветы. Луч лазера должен отклониться на экране после прохождения границы раздела.

Засеките время, в течение которого проходит процесс диффузии. Провал нужно наблюдать на экране по центру, чтобы в дальнейшем зарисовывать картину.

Спустя 30 минут обведите лазерный луч на миллиметровке, которая прикреплена к экрану. Эксперимент нужно выполнить для трех концентраций соли. Подпишите, какой концентрации соответствует каждый лист. В конических пробирках находятся растворы соли следующих концентраций: $C_1=153~\text{г/л}$, $С_2=187~\text{г/л}$, $C_3=220~\text{г/л}$.

B1  ^1.20 Зарисуйте на миллиметровке изображение лазерного луча, описанное выше, спустя 30 минут после начала процесса диффузии для всех трех концентраций соли.

B2  ^1.50 Запишите параметры установки $Z, d, Z_0$. Снимите с миллиметровки значения $\xi_i$ и $\delta_i$ (где $i=1,...20$~— нумерация точек по горизонтали) для всех трех значений концентрации соли. Величины должны быть выражены в миллиметрах.

B3  ^1.50 Вычислите величины $Y_i$ и $\left(\cfrac{dn}{dY}\right)_i$ для всех $i$. Постройте графики зависимости $\left(\cfrac{dn}{dY}\right)_i$ от $Y_i$.

B4  ^0.30 Для каждой концентрации соли определите $Y_i$ для которого $\left(\cfrac{dn}{dY}\right)_i$ максимально. Обозначьте это значение как $h$.

Кривые, полученные в пункте B3, могут быть описаны следующими уравнениями:
$$
\left(\cfrac{dn}{dY}\right)_i=\left(\cfrac{dn}{dC}\right)~\left(\cfrac{dC}{dY}\right)_i\quad\quad\quad\quad \left(\cfrac{dC}{dY}\right)_i=\cfrac{C_0}{2\sqrt{\pi Dt}}~\exp\left(-\cfrac{(h-Y_i)^2}{4Dt}\right),
$$
где $C$~— концентрация соли в растворе, $C_0$~— начальная концентрация соли в растворе, $D$~— коэффициент диффузии, $t$~— время диффузии, $h$~— значение $Y_i$ для максимального значения градиента показателя преломления $dn/dY$. Заметим, что $dn/dC$~— константа.

B5  ^0.90 Используя вышеприведенные уравнения, найдите функции $f(\cfrac{dn}{dY})$ и $g(Y)$, для которых зависимость $f(\cfrac{dn}{dY})$ от $g(Y)$ будет линейной.

B6  ^1.80 Пересчитайте данные из пункта B3 для построения линеаризованной зависимости. Постройте графики линеаризованных зависимостей.

B7  ^1.50 Определите коэффициенты диффузии по линейным участкам графиков, построенных в пункте B6.

B8  ^1.30 По результатам измерений для трех концентраций определите $dD/dC$.

Часть C. Псевдолинза Роберта Вуда (5 баллов)

Оборудование, используемое в этой части задачи: экран (2), держатель для фонарика (3), рулетка (4), отвертка (7), линейка (8), лезвие ножа (9), шприцы с желе (10), клейкая масса (11), прозрачные пластинки (12), крышка для резки желе (13), фонарик (14), сосуд с водой (15).

Линзы с переменным показателем преломления в настоящее время нашли применение в технике сантиметровых радиоволн. Для оптического диапазона электромагнитных волн изготовить подобную линзу, которая могла бы выдержать конкуренцию с обычными, довольно сложно. Однако выдающийся американский физик-экспериментатор Роберт Вуд за много лет до того, как появились первые радиолокационные станциии, следовательно, началось широкое применение сантиметровых радиоволн, предложил простую модель оптической линзы с переменным показателем преломления, которую он назвал псевдолинзой. Сегодня вам предстоит изготовить эту псевдолинзу из желатина.

Основная идея состоит в следующем. В шприцы залито желе, приготовленное на основе желатина и глицерина. Помещая желатиновый цилиндр в чистую воду, начинается процесс диффузии воды в цилиндр, а глицерина наружу. Т.к. показатели преломления глицерина и воды отличаются, после вымачивания в цилиндре образуется переменный показатель преломления.

Последовательность действий для изготовления псевдолинзы следующая:
1. Выдавите из шприца часть желатинового цилиндра и отрежьте кусочек нужной вам длины.
2. Поместите цилиндр между двумя прозрачными пластинами. Старайтесь не деформировать цилиндр. При необходимости в углы пластинок можно поместить клейкую массу, чтобы пластинки не разъезжались. На рисунке ниже: 1~— клейкая масс, 2~— желатиновый цилиндр, 3~— пластины.
3. Поместите цилиндр с пластинами в сосуд с водой на $t=(13.0\pm0.5)~\text{мин}$.
4. Достаньте цилиндр из воды. Он готов к измерениям.

C1  ^0.50 Схематично изобразите установку, с помощью которой вы будете определять фокусное расстояние изготовленной псевдолинзы. Буквами укажите параметры, которые вы будете измерять. Они должны соответствовать столбцам в таблице измерений.

C2  ^2.50 Получите значения фокусного расстояния $F$ для не менее 5 значений длины $l$ цилиндра (не забудьте привести данные прямых измерений). Длина цилиндра должна быть от 2 до 6 мм. Для каждого значения длины проведите не менее трех измерений. Усредните значения фокусных расстояний, укажите статистический разброс и оцените погрешность определения фокусного расстояния.

Можно считать, что для псевдолинзы радиуса $R$ равны оптические пути от источника на бесконечности до фокуса для лучей, проходящих через центр и через край линзы.

C3  ^1.00 Выразите $\Delta n$~— разницу между коэффициентом преломления~$n(0)$ в центре и коэффициентом преломления $n(R)$ на краю линзы через толщину линзы $l$, фокусное расстояние $F$ и радиус линзы~$R$. Считайте, что $\Delta n \ll n$, а внутренний диаметр шприца, из которого выдавливаются цилиндры, равен $D=8.8~\text{мм}$.

C4  ^1.00 Постройте линеаризованную зависимость $F$ от $d$ с помощью результата из пункта C3. Найдите $\Delta n$. Оцените погрешность.