На гладкой горизонтальной поверхности лежит «двойная гантель»~— система, состоящая из двух лёгких стержней длины $L$, соединённых шарниром массы $2m$. На свободных концах стержней закреплены грузы массы $m$.В этой задаче исследуется движение данной системы при разных условиях.

Часть A. Движение на поверхности (2.0 балла)

В начальный момент грузы и шарнир лежат на одной прямой. В некоторой момент один из стержней начинают вращать с постоянной угловой скоростью $\omega$, причём груз на его конце всё время неподвижен. В этой части задачи необходимо найти угловую скорость вращения второго стержня в разные моменты движения. Считайте известным, что угловая скорость - векторная величина,направленная перпендикулярно плоскости движения( для первого стержня она сонаправлена с осью $OZ$ и равна $\vec\omega$).Также считайте известным закон сложения угловых скоростей
$$\vec\omega=\vec\omega_{отн}+\vec\omega_{пер}
$$
где $\vec\omega_{пер}$ - угловая скорость вращающейся системы отсчёта, $\vec\omega_{отн}$ - угловая скорость движения относительно вращающейся системы отсчёта.

A1  ^0.30 Найдите вектор угловой скорости второго стержня в начальный момент времени. Ответ выразите через $\vec\omega$.

Перейдём во вращающуюся систему отсчёта, связанную с первым стержнем. Во вращающейся системе отсчёта на груз второго стержня в плоскости движения помимо силы его натяжения действуют центробежная и Кориолисова силы. Влияние Кориолисовой силы в данной задаче учитывать не нужно,поскольку она перпендикулярна скорости груза и не меняет его кинетическую энергию.Напомним выражение для центробежной силы
$$\vec{F_{цб}}=m{\omega}^2\vec{r}
$$
где $\vec{r}$ - радиус-вектор груза во вращающейся системы отсчёта, проведённый из начала координат.

A2  ^0.20 В начальный момент времени найдите вектор угловой скорости $\vec\omega_{отн_0}$второго стержня в системе отсчёта, связанной с первым стержнем. Ответ выразите через $\vec\omega$

A3  ^0.50 Найдите потенциальную энергию груза в поле центробежной силы на расстоянии $r$ от оси вращения с точностью до произвольной постоянной. Ответ выразите через $m$, $\omega$, $r$.

A4  ^0.50 Пусть второй стержень повернулся на угол $\varphi$ относительно первого. Найдите его угловую скорость $\omega_{отн}$ в данном положении. Ответ выразите через $\omega$ и $\varphi$.

Теперь вам предстоит скорость груза в неподвижной системе отсчёта. Используйте закон сложения скоростей для вращающихся систем отсчёта.

A5  ^0.50 Найдите скорость груза в неподвижной системе отсчёта. Ответ выразите через $\omega$, $L$, $\varphi$.

Часть B. Движение в вертикальной плоскости(4.2 балла)

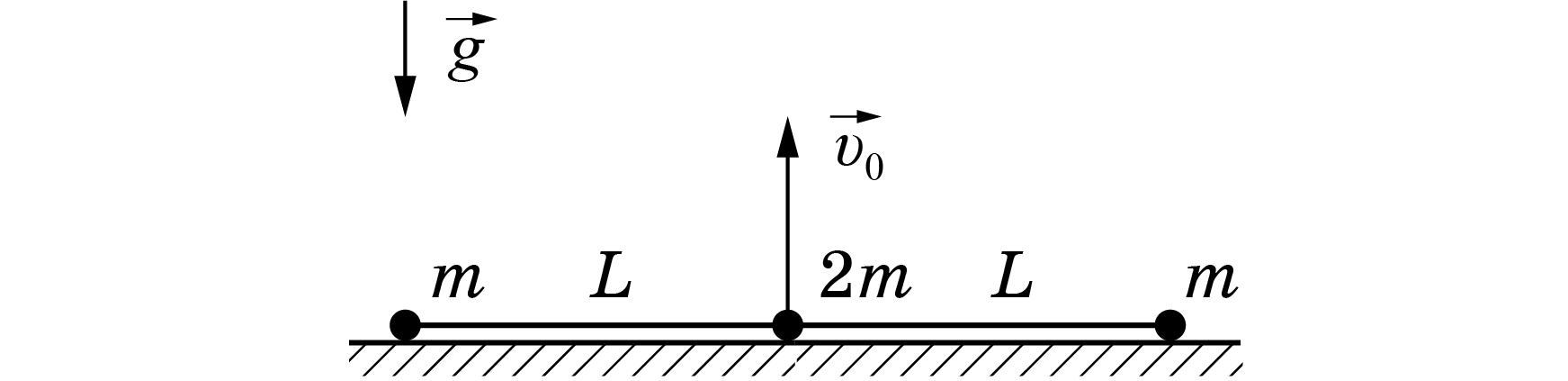
В этой части задачи в начальный момент времени грузы и шарнир находятся на одной прямой и шарниру сообщается скорость $v_0$, направленная вертикально вверх. Вам предлагается исследовать дальнейшее движение такой системы. Пусть в некоторый момент времени стержни образуют угол $\varphi$ с горизонтом.
Ось $OX$ направлена горизонтально, а ось $OY$ - вертикально вверх.

B1  ^0.40 Обозначим силу натяжения стержней за $T$
$$
$$
Найдите ускорения грузов $a_{1л}$,$a_{1п}$ в проекции на ось $OX$ и ускорение шарнира $a_2$ в проекции на ось $OY$.Ответы выразите через $m$.$g$.$T$ и $\varphi$.

B2  ^0.60 В указанном положении найдите скорости грузов $v_1$ и скорость шарнира $v_2$.

B3  ^1.00 Запишите уравнение движения шарнира относительно любого из грузов,связывающее $v_1$,$v_2$,$a_1$,$a_2$,$L$ и $\varphi$

B4  ^0.70 Найдите силу натяжения $T$ из уравнения,полученного в пункте $B3$.Ответ выразите через $m,{v_0},g,L,{\varphi}$

B5  ^1.00 Предположим, что в некоторый момент грузы отрываются от поверхности.
$$
$$
Найдите значение угла $\varphi_{отр}$ в этот момент времени.

B6  ^0.50 Найдите минимальное значение $v_0$, при котором грузы оторвутся от поверхности и значение угла $\varphi' $ в момент отрыва

Часть C.Грузы в лёгких упругих оболочках(3.8 балла)

Данная часть задачи является фактическим продолжением предыдущей.Отличие состоит в том, что теперь грузы находятся в центрах лёгких упругих оболочек радиуса $R<{L}$.Предполагается, что скорость $v_0$ шарнира достаточна для того, чтобы в части $B$ грузы оторвались от поверхности.Обозначим за ${\varphi_0}$ угол стержней с горизонтом в момент касания оболочек.

C1  ^0.20 При каких значениях $R$ столкновение оболочек происходит раньше их отрыва от поверхности под действием стержней? Ответ выразите через $L$,$\varphi_{отр}$,

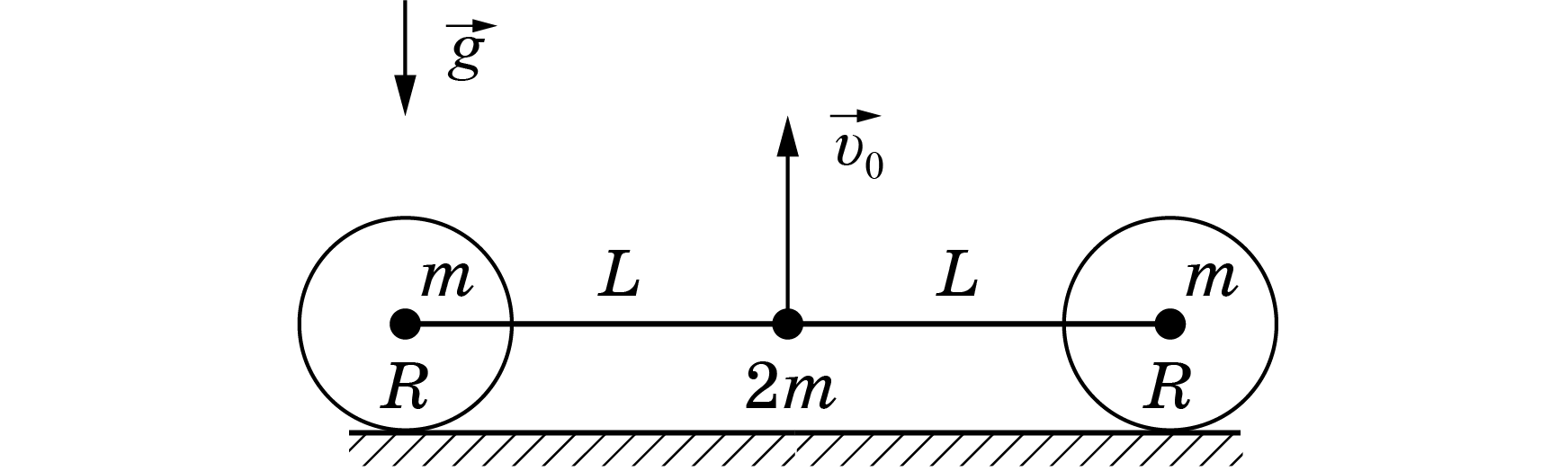
В дальнейшем считайте, что условие на $R$, полученное в предыдущем пункте выполняется.

C2  ^1.00 Пусть сразу после столкновения проекции скорости груза на оси $OX$ и $OY$ равны $v_{1x}$ и $v_{1y}$ соответственно.
$$
$$
Выразите проекцию скорости шарнира на вертикальную ось $v_{2y}$ через $v_{1x}$,$v_{1y}$ и ${\varphi_0}$.

C3  ^1.30 Найдите скорость шарнира $v_2$ сразу после соударения. Ответ выразите через ${v_0},g,{L},R$

C4  ^1.30 Найдите модуль скоростей грузов $v_1$ сразу после соударения.Ответ выразите через ${v_0},g,{L},R$