Солнце представляет массивное небесное тело, состоящее из плазмы. Плазма имеет высокую электропроводность, поэтому в ней могут возникать электрические токи и, как следствие, магнитные поля. В минимуме цикла солнечной активности оно имеет приблизительно дипольную структуру, при этом индукция поля на полюсах Солнца максимальна. На поверхности Солнца наблюдаются солнечные пятна — тёмные области на Солнце, температура которых заметно ниже по сравнению с окружающими участками поверхности Солнца. Потемнение в пятнах обусловлено подавлением магнитным полем конвективных движений вещества и, как следствие, снижением потока переноса тепловой энергии в этих областях.

Часть А. Вращение поверхности Солнца (2.3 балла)

Солнце не является твёрдым телом, оно состоит из газообразной плазмы. Точки на разных широтах вращаются с разными периодами, то есть вращение Солнца является дифференциальным. Скорость вращения $\omega$ является наибольшей на экваторе $\varphi=0^\circ$ Солнца и уменьшается при движении к полюсам $\varphi=\pm90^\circ$. В достаточно широкой окрестности экватора применима формула
\[
\omega(\varphi) = a - b \sin^2\varphi
\]

A1  ^2.00 Вам представлена таблица экспериментальных данных $\omega(\varphi)$. Данные получены исходя из эффекта Доплера, влияющего на частоту электромагнитного излучения Солнца, регистрируемого на Земле. Определите параметры $a$ и $b$.

A2  ^0.30 Найдите границы применимости формулы, указанной выше.

Часть В. Начальное состояние (1.6 балла)

В момент минимума солнечной активности будем считать магнитное поле Солнца за его пределами полем диполя с магнитным моментом $\vec{\mathfrak{M}}$. Этот магнитный момент направлен вдоль оси вращения Солнца. Будем называть компоненты поля $B_r$ — направленное вдоль радиуса, $B_\varphi$ — направленное вдоль увеличения широты, $B_\lambda$ — направленное вдоль увеличения долготы.

B1  ^0.30 Получите все составляющие магнитного поля на поверхности Солнца $B_{0,r}(\phi)$, $B_{0,\phi}(\phi)$, $B_{0,\lambda} (\phi)$. Ответы выразите через $\varphi$, $\mathfrak{M}$, $R_0$ и $\mu_0$.

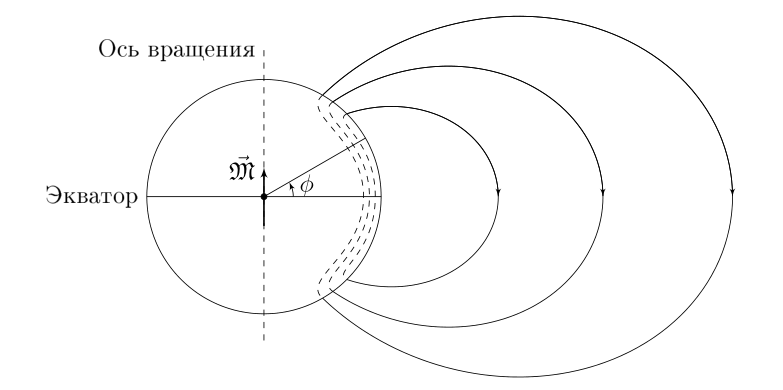
Магнитные линии внутри Солнца проходят перпендикулярно радиус-вектору в слое толщиной $H(\varphi) = H_0 \cos^2 \varphi$, где $H_0 = \xi R_0$, $\xi=0.05 \ll 1$ и лишь у самого выхода из поверхности закругляются. Считайте, что поле $B$ внутри Солнца равномерно по этому тонкому слою, в котором локализованы магнитные линии. Модуль потока $\Phi_0$ магнитного поля через северное полушарие Солнца равен $8.0\cdot10^{13}~\text{Вб}$. Радиус Солнца $R_0=6.96\cdot 10^8~\text{м}$.

B2  ^0.60 Получите величину магнитного поля $B_e$ на экваторе внутри Солнца у его поверхности. Ответ выразите через $\mathfrak{M}$, $\mu_0$, $R_0$, $\xi$.

B3  ^0.10 Найдите численное значение $B_e$.

B4  ^0.60 Получите величину магнитного поля $B_\varphi(\varphi)$ внутри Солнца у его поверхности в зависимости от широты $\varphi$. Ответ выразите через $\varphi$, $B_e$.

Часть С. Закручивание магнитных линий (3.2 балла)

Малые магнитные поля (порядка $B_e$) можно считать вмороженными в плазму в том смысле, что магнитные линии искажаются при относительном движении плазмы. Это значит, что если через точки $A$ и $B$ в начальный момент времени $t=0$ проходит линия магнитного поля, то и в любой другой момент времени она будет через них проходить. В силу того, что у разных точек поверхности Солнца разная угловая скорость, магнитные линии внутри поверхности Солнца будут искажаться. При этом внешнее поле останется таким же. Момент времени, описанный в части А обозначим за $t=0$.

C1  ^1.70 Точно рассчитайте 30 пар точек $(\varphi, \lambda)$, через которые будет проходить магнитная линия, пронизывающая точки $\varphi=\pm 50^\circ$, $\lambda=0$ в момент времени $t=150~\text{дней}$.

C2  ^1.00 Используя эти данные постройте в листе ответов, как будет выглядеть эта линия для земного наблюдателя.

Меридианом называется линия, для которой $\lambda=\text{const}$. Также эта линия получается при пересечении сферы и плоскости, проходящей через ось вращения сферы.

C3  ^0.30 Найдите угол $\psi (\varphi,t)$, который составляют магнитные линии с меридианом. Ответ выразите через $\varphi$, $t$, $a$, $b$.

С4  ^0.20 Пусть внутри Солнца вблизи его поверхности магнитные линии составляют угол $\psi$ с меридианом. Найдите модуль магнитного поля $B$ в этой точке. Ответ выразите через $\psi$, $\varphi$, $B_e$.

Часть D. Образование солнечных пятен (2.9 балла)

Солнечные пятна на поверхности Солнца образуются, когда магнитное поле внутри Солнца превышает $B_\text{крит}$. В каждом последующем пункте Вы можете использовать диаграмму Маундера, на которой цветом указана доля поверхности Солнца (чем темнее, тем больше доля), покрытая солнечными пятнами, а по осям отложены $t$ и $\sin \varphi$.

D1  ^2.70 Используя приближение $\sin \psi \approx 1 $, найдите $B_\text{крит}$.

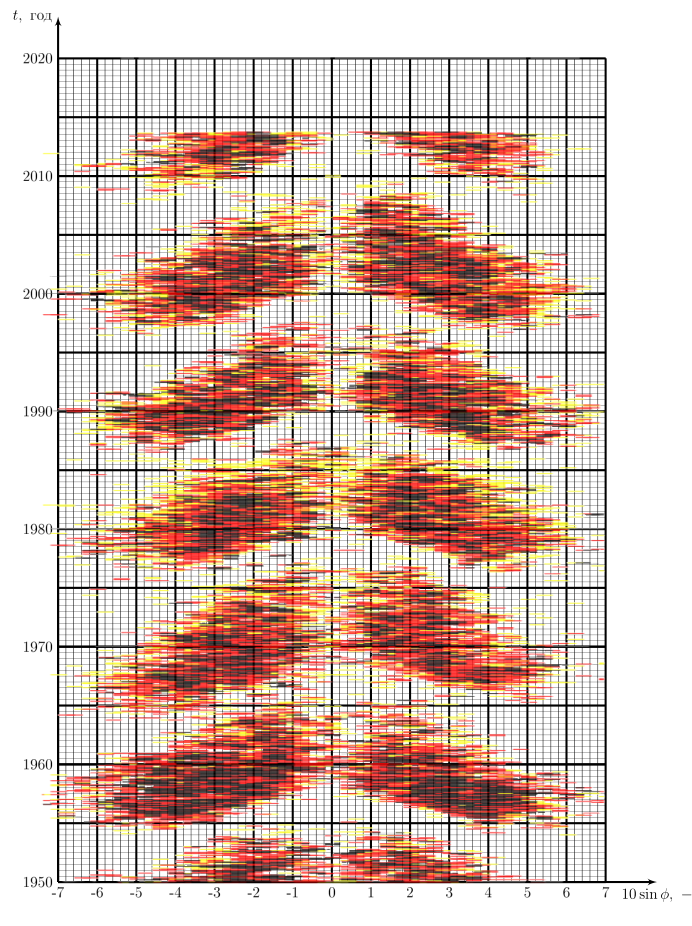
При сильном увеличении поля $B$ внутри Солнца перестает работать модель, описанная ранее в части С. Магнитные линии начинают закручиваться вокруг себя и дипольное магнитное поле подавляется. Из-за этого солнечные пятна начинают пропадать, т.к. величина поля уменьшается. В результате система приходит в начальное состояние с точностью до того, что меняется направление вектора $\mathfrak{M}$ на противоположное. Таким образом наша система периодична.

D2  ^0.20 Определите период солнечной активности $T_0$, т.е. время через которое магнитное поля Солнца возвращается в исходное состояние.