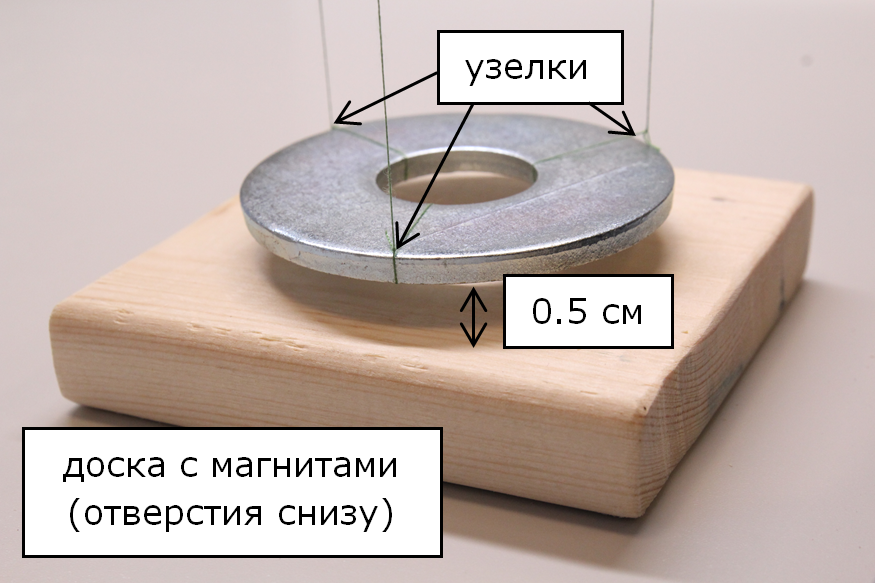
Трифилярный подвес (см. рис. ниже) используют для изучения крутильных колебаний. Вводные части этой экспериментальной задачи посвящены сборке крутильного маятника и проведению с ним простейших измерений, потребуется также теоретически получить выражение для периода колебаний. Затем собранная установка будет использоваться для изучения структуры более сложных объектов. В части, посвященной эллипсоиду инерции, будут исследоваться колебания бруска при разных его ориентациях в пространстве. Последние две части эксперимента позволят оценить влияние вязкого трения или магнитного взаимодействия на затухание колебаний.

1. штатив с муфтой и лапкой
2. верхний диск (толще)
3. нижний диск (тоньше и с окружностями, его масса всюду обозначена $m_0$)
4. линейка $50~\text{см}$
5. нитки
6. ножницы
7. канцелярская клипса
8. секундомер
9. гвоздь для закрепления петелек под нижним диском
10. гайки в зажимах A и B
11. брусок с пластинами
12. зажим для ориентирования вращаемого тела в пространстве
13. шайба (в частях F и G можно считать ее массу известной и равной $m_\text{ш} = 80~\text{г}$)
14. контейнер, вода по требованию (для части F)
15. картонный транспортир
16. бумажные салфетки для поддержания чистоты рабочего места
17. доска с магнитами
$\textbf{Оценка погрешностей не требуется ни в одной из частей этой работы!}$
В оборудовании есть мелкие детали, не теряйте их.
Будьте аккуратны с изделиями из оргстекла. Сломанные или треснувшие элементы заменяться не будут!
Вскрывать черные треугольные зажимы с гайками запрещено!

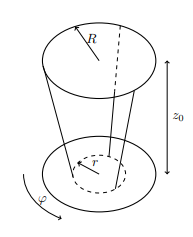
Пусть верхние и нижние концы нитей трифилярного подвеса закреплены на расстояниях $R$ и $r$ от оси соответственно. При неизменных остальных параметрах установки период крутильных колебаний такого маятника зависит от $R$ и $r$ следующим образом: $T=C \cdot R^\alpha r^\beta$.
$\textit{Примечание.}$ Сменить $r$ удобно следующим способом. Петельки на нижних концах диска снимаются с гвоздика, вынимаются из «старых» дырок и пропускаются через «новые», после чего обратно фиксируются на гвоздик. Поскольку длина подвеса при этом меняется, необходимо ослабить клипсу и скорректировать намотку трёх верхних концов нитей.
Вам выданы две различные гайки в треугольных зажимах A и B. Общие массы гаек в зажимах равны $m_A$ и $m_B$. Каждая гайка содержит пустую цилиндрическую полость (ось цилиндра совпадает с осью гайки). Считайте, что все грани гайки — плоские (скругления не учитывайте), поверхность внутренней цилиндрической полости — гладкая (резьбу не учитывайте). Ваша цель — определить радиусы $a$ и $b$ цилиндрических полостей в гайках A и B соответственно. Для измерении периода колебаний гайку располагайте на нижнем диске собранного трифилярного подвеса (плоскость треугольных оснований должна быть параллельна плоскости диска).
$\textit{Внимание!}$ В этой части, а также в части D, для удобства пользования установкой следует взять $r$ максимально возможным.
С2
3.80
Проведите точные измерения периодов колебаний гаек.
Определите $a$ и $b$.
Опишите проводимые вами измерения. Приведите их результаты, в т.ч. геометрические параметры гаек, а также предоставьте все используемые вами теоретические выкладки и расчеты. Запишите, какие значения $r$ и $z_0$ вы выбираете при сборке установки для этого пункта.
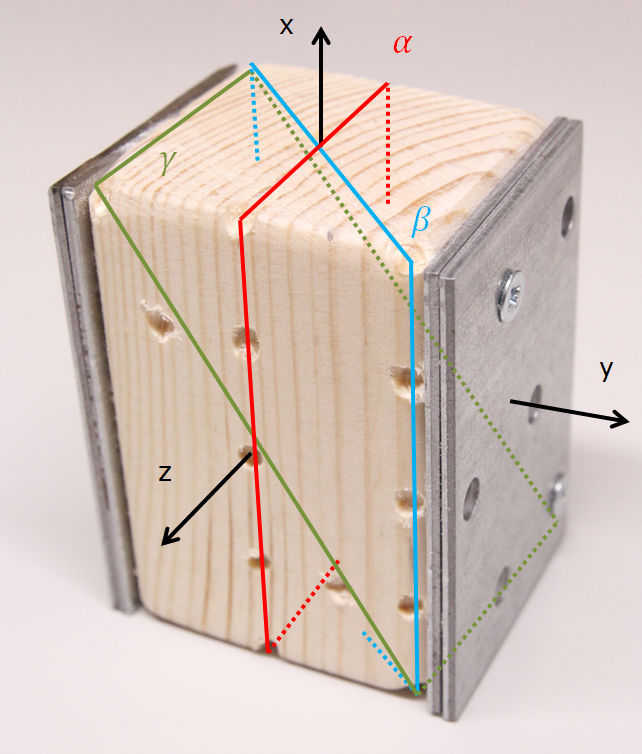
К двум граням деревянного бруска прикреплено по 2 стальные пластины. Масса бруска $M_\text{бр}$, масса каждой из четырех пластин $M_\text{пл}$. Массой и моментом инерции скрепляющих винтов следует пренебречь.
$\textit{Внимание!}$ В этой части, как и в части D, для удобства пользования установкой следует взять $r$ максимально возможным.
D2
2.40
Выразите теоретически моменты инерции $I_x$, $I_y$, $I_z$ (см. рисунок выше) бруска с пластинами через его стороны $a$ и $b=с$, толщину металлической пластины $d=1.8~\text{мм}$, а также $M_\text{пл}$, $M_\text{бр}$. Получите систему уравнений, из которой можно будет найти отношение $M_\text{пл}/M_\text{бр}$.
Предоставьте все используемые вами теоретические выкладки и расчеты.

$\textit{Внимание!}$ В дальнейших пунктах этой части пренебрегайте массой и моментом инерции зажима.
В бруске намечены отверстия, в которые можно упирать зажимающие винты зажима. Закрепляя брусок в разных пространственных ориентациях, можно провести измерения и рассчитать моменты инерции бруска $I$ относительно множества различных осей, проходящих через его центр. На фотографии выше отмечены буквами $\alpha$, $\beta$, $\gamma$ три плоскости, рассекающие брусок и проходящие через его центр.
E2
1.00
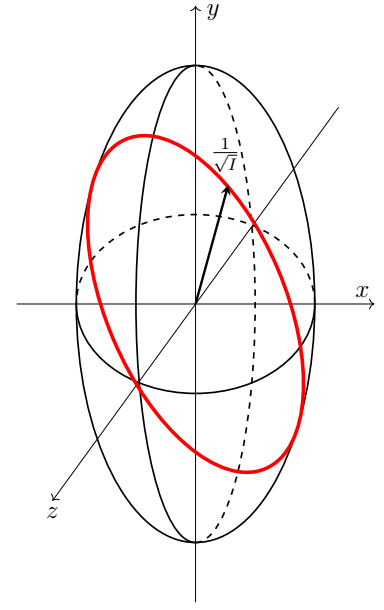
Для каждой из 6 осей в сечении $\alpha$ проведите точные измерения периода колебаний и рассчитайте величину $\cfrac{1}{\sqrt{I/m}}$.
Для каждой из осей на приведенной в листе ответов диаграмме (совпадающей с сечением $\alpha$ и нарисованной с соблюдением пропорции сторон) отложите от центра отрезок, равный $\cfrac{1}{\sqrt{I/m}}$, в обе стороны вдоль направления соответствующей оси. Обведите полученные 12 «внешних» концов отрезков единой замкнутой кривой.
F3
1.30
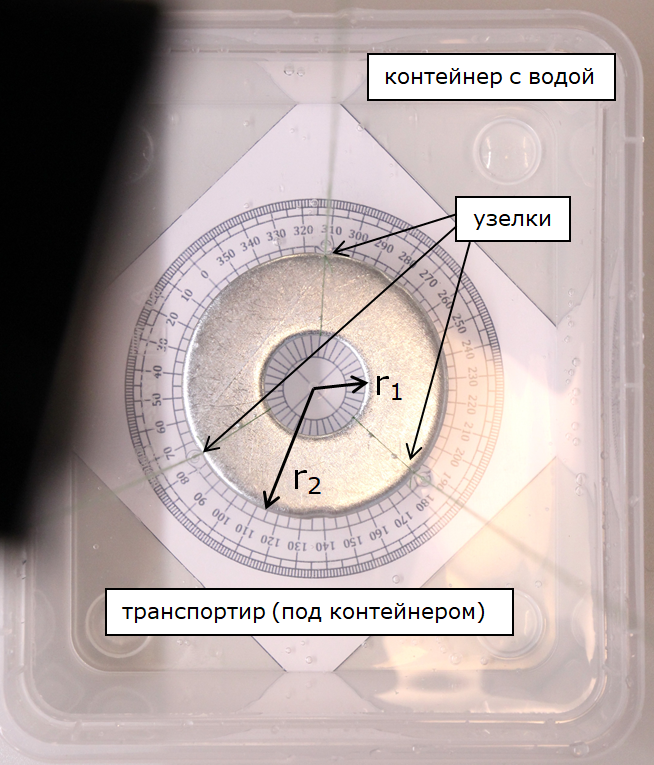
Решите теоретическую задачу. Пусть тонкая шайба с внутренним и внешним радиусами $r_1$ и $r_2$ соответственно колеблется в толще воды, за счет вязкого трения приводя в движение с некоторыми скоростями слои воды на глубинах от $(H-h)$ до $(H+h)$, где $H$ — глубина погружения шайбы, $h$ — условная суммарная толщина движущихся слоёв. Вязкость воды $\eta=8.9\cdot 10^{-4}~\text{Па}\cdot\text{с}$, ускорение свободного падения $g=9.81~\text{м} / \text{с}^2$.
Какой момент сил вязкого трения $M$ действует на шайбу в момент, когда она вращается с угловой скоростью $\dot{\varphi}$? Выразите $M$ через $\dot{\varphi}$, $\eta$, $h$, $r_1$, $r_2$.
Выразите логарифмический декремент затухания $d$ колебаний с вязким трением через $\eta$, $h$, $r_1$, $r_2$, $m$, $T$.
$\textit{Примечание.}$ Логарифмическим декрементом затухания называется логарифм отношения амплитуд последовательных колебаний: $d=\text{ln}\cfrac{\varphi_i}{\varphi_{i+1}}$.
F4
1.00
Как вы заметили, колебания довольно быстро затухают. Пусть $\varphi(i)$ - амплитуда $i$-го колебания. Снимите зависимость $\varphi(i)$. Возможно, для этого потребуется несколько раз запускать колебания с одинаковыми начальными условиями. Постройте линеаризованный график и по нему рассчитайте логарифмический декремент затухания $d$.