A1  ^1.70 При фиксированном $R$ проведите точные измерения периода $T(r)$. Запишите, какие значения $r$ и $z_0$ вы выбираете при сборке установки для этого пункта, и чему равно измеренное вами $R$. Постройте линеаризованный график и определите $\beta$.

Соберем установку с $z_0 = 50.0~\text{см}$ и после каждого изменения $r$ будем корректировать длину нитей так, чтобы $z_0$ оставалось прежним. Измерим расстояние от верхнего конца нитей до оси установки: $R = 5.0~\text{см}$. Для каждого из доступных $r$ измерим суммарное время $N$ колебаний. Поскольку зависимость $T(r)$ имеет описанный в условии вид $T=C \cdot R^\alpha r^\beta$, для ее линеаризации построим график $\ln T (\ln r)$. Его угловой коэффициент будет равен $\beta$.

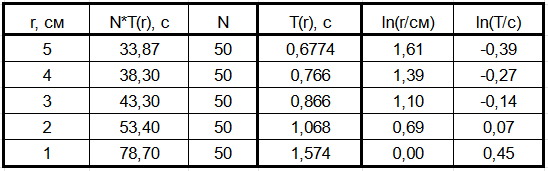
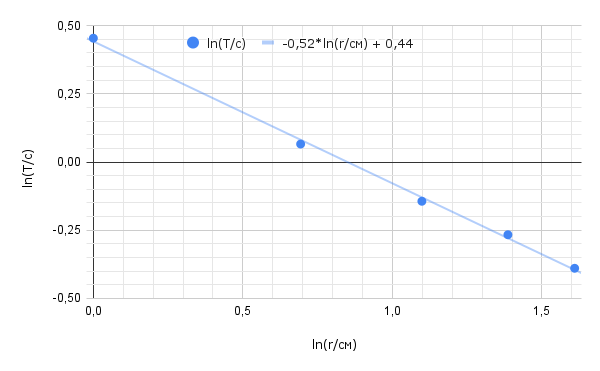
По графику определяем $\beta = -0.52 \approx -0.5$.

A2  ^0.30 Чему равна $\alpha$? Объясните свой ответ.

Для обоснования этого равенства можно привести любой из следующих аргументов:

1. Геометрия установки определяется величинами $R$ и $r$ равноправно. Например, на высоту подъема нижнего диска при его повороте на фиксированный угол влияют оба этих радиуса, и высота не изменится при "перевороте" установки. Таким образом, $R$ и $r$ должны входить в формулу для $T$ симметрично, и формула не должна меняться при замене $R\leftrightarrow r$.

2. Попробуем "угадать" примерный вид формулы $T (R, r, z_0, I, m, g)$. По аналогии с периодом колебаний математического маятника, а также с учетом найденного $\beta = -0.5$, имеем: $T \propto \sqrt{\cfrac{z_0}{gr}}$. Чтобы размерность массы сократилась, в формулу должно входить отношение $I/m$. Также, по условию, $T \propto R^\alpha$. Причем ясно, что при увеличении момента инерции, а также при уменьшении $R$, период возрастет. Таким образом, имеем:
$$T \propto \sqrt{\cfrac{z_0}{gr} \cdot \left( \cfrac{I}{m} \right)^\gamma}\cdot \cfrac{1}{R^{|\alpha|}},$$
где $\gamma>0$.
Применим метод размерностей:
$$с = \sqrt{\cfrac{\text{с}^2}{\text{м}} \cdot \left(\text{м}^2 \right) ^\gamma}\cdot \cfrac {1}{\text{м}^{|\alpha|}}$$
Получаем условие на степени: $2\gamma = 1+2|\alpha|$. Простейшее решение этого уравнения: $\alpha = -0.5$, $\gamma = 1$. Для подтверждения выбора такой пары корней можно провести, например, аналогию с формулой колебанияй стержня, подвешенного на двух нитях.

3. Явная формула, которая будет получена в пункте B3, подтверждает найденный ранее коэффициент $\beta = -0.5$ и дает $\alpha = -0.5$.

B1  ^0.60 Введите Декартову систему координат и запишите координаты верхнего и нижнего концов одной из нитей. Выразите расстояние $L$ между ними через $R$, $r$, $z_0$, $h$, $\varphi$.

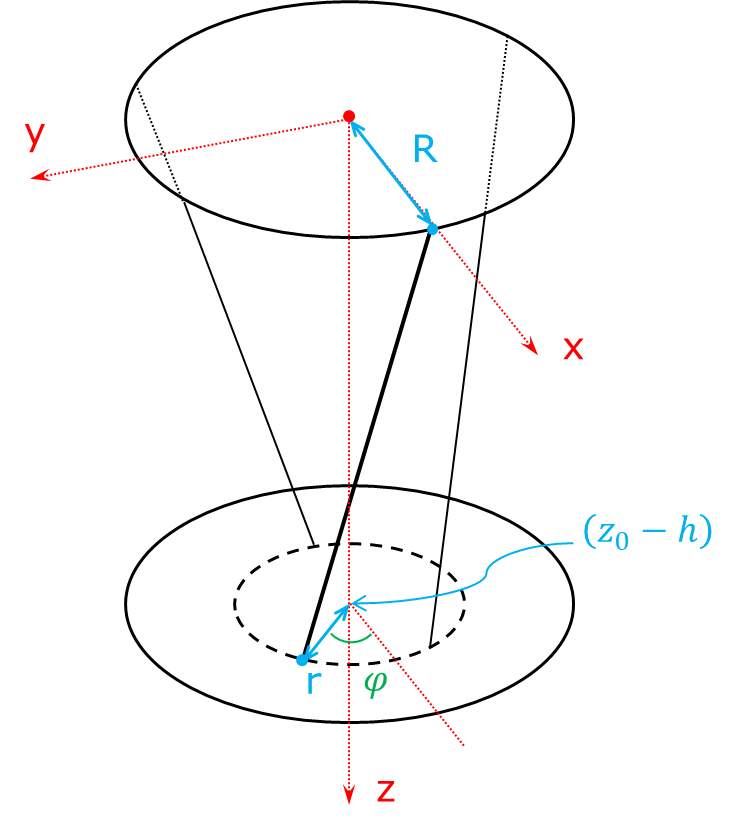
Введем систему координат, например, связанную с верхним радиус-вектором и с осью $z$, направленной вниз (см. рис.).
Кординаты верхнего конца выделенной на рисунке нити:
$X=R$
$Y=0$
$Z=0$
Нижний конец нити:
$x=r\cdot \cos\varphi$
$y=r\cdot \sin\varphi$
$z=z_0-h$

По теореме Пифагора выражаем длину нити:

B2  ^0.60 Нити нерастяжимы и при колебаниях всегда натянуты. Используя это, выразите $h$ через $R$, $r$, $z_0$, $\varphi$. Напоминаем, что угол $\varphi$ мал.

В положении равновесия $\varphi = 0$ и $h = 0$, а длина нити $L_0 = \sqrt{(R-r)^2 + z_0^2}$. Нити нерастяжимые и при колебаниях всегда натянуты, значит $L=L_0$:
$$(R-r\cos{\varphi})^2 + (r\sin{\varphi})^2 + (z_0-h)^2 = (R-r)^2 + z_0^2$$
$$(R-r\cos{\varphi})^2 + (r\sin{\varphi})^2 - (R-r)^2 = z_0^2 - (z_0-h)^2$$
$$-2Rr\cos{\varphi} + 2Rr = 2z_0h - h^2$$
$$2Rr~(1-\cos{\varphi}) = 2z_0h - h^2$$
При $\varphi \ll 1$ и $h \ll z_0$ можем отбросить все порядки их малости, кроме первых ненулевых:
$$2Rr \cdot \cfrac{\varphi^2}{2} = 2z_0h$$
Окончательно:

B3  ^0.80 С помощью закона сохранения энергии при крутильных колебаниях получите выражение для $T$ через $R$, $r$, $z_0$, $I$, $m$, $g$.

Запишем закон сохранения энергии, пренебрегая вертикальным движением центра масс:
$$\cfrac{I\left(\dot \varphi \right)^2}{2} + mgh = const$$
$$\cfrac{I\left(\dot \varphi \right)^2}{2} + mg\cfrac{Rr}{z_0} \cfrac{\varphi^2}{2} = const$$
Дифференцируем это уравнение по времени:
$$\cfrac{I \cdot 2 \dot \varphi \ddot \varphi}{2} + mg\cfrac{Rr}{z_0} \cfrac{2\varphi \dot \varphi}{2} = 0$$
И сокращаем на не равную тождественно нулю функцию $\dot \varphi (t)$:
$$I \ddot \varphi + mg\cfrac{Rr}{z_0} \varphi = 0$$
$$\ddot \varphi = - \cfrac{mgRr}{z_0I} \varphi$$
Получилось уравнение гармонических колебаний, по нему легко определить их период:

Видно, что полученные в части A результаты $\alpha = \beta = -\cfrac{1}{2}$ согласуются с теорией.

C1  ^0.20 С помощью рычага определите отношения $m_A/m_0$ и $m_B/m_0$ как можно точнее.

Сделаем из линейки симметричный рычаг. К одному из концов линейки подвесим на нитях диск трифилярного подвеса, на другом плече "взвесим" по очереди обе гайки. Уравновешивая рычаг в обоих случаях, получаем соотношения:

С2  ^3.80 Проведите точные измерения периодов колебаний гаек.

Определите $a$ и $b$.

Опишите проводимые вами измерения. Приведите их результаты, в т.ч. геометрические параметры гаек, а также предоставьте все используемые вами теоретические выкладки и расчеты. Запишите, какие значения $r$ и $z_0$ вы выбираете при сборке установки для этого пункта.

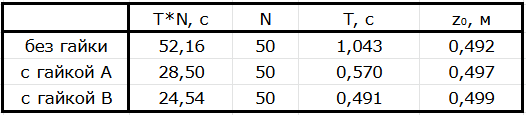
Будем использовать $z_0 \approx 49~\text{см}$ и $r = R = 5.0~\text{см}$. Нити немного растягиваются под действием помещенного на трифилярный подвес груза, поэтому точные значения $z_0$ будем проверять для каждого отдельного эксперимента. В таблице приведены результаты измерений периода крутильных колебаний как пустой платформы трифилярного подвеса, так и платформы с каждой из гаек. Как и прежде, измеряется суммарное время $N$ колебаний. Также измерим линейкой расстояние $3.5~\text{см}$ между противоположными сторонами 6-угольной гайки, отсюда сторона 6-угольника равна $s = \cfrac{3.5~\text{см}}{\sqrt 3} = 2.02~\text{см}$.

Выведем теоретические формулы, позволяющие рассчитать $a$ и $b$.
Масса гайки выражается через сторону 6-угольника $s$ и радиус отверстия $a$ следующим образом:
$$m_A=\rho\cdot \left( \cfrac{3\sqrt{3}}{2}s^2 H - \pi a^2 H\right)$$

Для расчета момента инерции гайки вычислим сначала момент инерции плоского треугольника со стороной $s$ относительно его центра. Для этого разделим треугольник средними линиями на 4 треугольника меньшего размера: масса каждого из них равна $m_\Delta/4$, сторона каждого равна $s/2$. Если момент инерции большого треугольника равен $\alpha \cdot m_\Delta s^2$ (из соображений размерности), где $\alpha$ — некий числовой коэффициент, то момент инерции каждого из меньших треугольников относительно своего центра равен $\alpha \cdot \cfrac{m_\Delta}{4} {\left(\cfrac{s}{2}\right)}^2$. Их суммарный момент инерции, равный, с одной стороны, $\alpha \cdot m_\Delta s^2$, можно, с другой стороны, выразить через моменты инерции меньших треугольников (с учетом добавок Гюйгенса-Штейнера):
$$I_\Delta = \alpha m_\Delta s^2 = 3\cdot \left( \alpha \cfrac{m_\Delta}{4} {\left(\cfrac{s}{2}\right)}^2 + \cfrac{m_\Delta}{4} {\left( \cfrac{s}{2\sqrt 3} \right)}^2 \right) + \alpha \cfrac{m_\Delta}{4} {\left(\cfrac{s}{2}\right)}^2.$$
После сокращения на $(m_\Delta s^2)$:
$$\alpha = 3\cdot \left( \alpha \cfrac{1}{16} + \cfrac{1}{48} \right) + \alpha \cfrac{1}{16},$$ откуда $\alpha = \cfrac{1}{12}$. Итого, для треугольника относительно его центра: $I_\Delta=\cfrac{1}{12}m_\Delta s^2$. Тогда относительно вершины: $I_\Delta=\cfrac{5}{12}m_\Delta s^2$. Аналогичное выражение для момента инерции треугольной призмы при ее вращении вокруг оси, совпадающей с одним из боковых ребер.

Момент инерции гайки, если ее приблизить 6-угольной призмой (состоящей из шести треугольных) с цилиндрическим отверстием, выражается следующим образом:
$$I_A = \rho \left( \cfrac{5}{12} s^2 H \cfrac {3\sqrt{3}}{2}s^2 - \cfrac{1}{2} \pi a^2 H a^2 \right).$$


Объединяя в одно уравнение неизвестный радиус отверстия $a$ и измеряемые величины, получаем биквадратное уравнение на $a$:
$$a^{4} -2 \kappa a^{2}+\frac{3 \sqrt{3}}{\pi} \cdot s^{2} \left(\kappa-\frac{5}{12} s^{2}\right)=0,$$ где
$$\kappa=Rr g \left( \left(\frac{T_A}{2 \pi}\right)^{2} \cdot \frac{\frac{m_{0}}{m_A}+1}{z_{0A}}- \left( \frac{T_{0}}{2 \pi} \right) ^2 \cdot \frac{\frac{m_{0}}{m_A}}{z_{0}}\right).$$ Здесь через $T_0$ обозначен период колебаний подвеса без гайки, $T_A$ — с гайкой, $m_0$ — масса линейки, $z_0$ — длина нитей подвеса, $z_{0A}$ — длина растянувшихся под весом гайки нитей подвеса.

Аналогичное уравнение для гайки B можно получить из этого, если заменить $a$ на $b$ и сменить индексы $A \to B$.

Рассчеты по приведенным формулам для гайки A дают два ответа:
$a_1 = \sqrt{a_1^2} = 1.2~\text{см}$ и $a_2 = \sqrt{a_2^2} = 1.8~\text{см}$.
Заметим, что расстояние от центра гайки до середины ее грани (при $s = 2.0~\text{см}$) равно $1.7~\text{см}$, что меньше предполагаемого вторым ответом отверстия, поэтому $a_2$ соответствует не реализуемому на практике случаю и мы вынуждены выбрать ответ $a_1$.

$\textit{Примечание.}$ Полученное число хорошо соответствует среднему радиусу $1.15~\text{см}$ нарезанной в гайке метрической резьбы.

Для гайки B один из ответов отпадает по той же причине, остается вариант $b_1 = 3.9~\text{мм}$. Фактически при изготовлении гайки B в нее был вкручен отрезок шпильки соответствующего диаметра, так что отверстие в ней отсутствует вовсе. Возможные небольшие отклонения рассчитанного радиуса $b$ от нулевого значения могут проявляться по нескольким причинам: неплотная резьба, разброс длины нарезаемых отрезков шпильки, пренебрежение массой зажимов гайки, неточное измерение ее сторон.

D1  ^0.40 Проведите точные измерения периодов колебаний при установке бруска с пластинами на грань с пластинами ($T_y$), а также при установке на одну из других граней ($T_x$ или $T_z$). Запишите, какие значения $r$ и $z_0$ вы выбираете при сборке установки для этого пункта.

Результаты измерений приведены в таблице, причем $T_0$ - период колебаний пустого диска. По-прежнему, $r = 5.0~\text{см}$. Нити немного растягиваются при установке бруска на диск, поэтому значение $z_0$ различается для измерений с бруском и без него. Измерим линейкой габариты бруска: $a = 60~\text{мм}$, $b=c=40~\text{мм}$.

D2  ^2.40 Выразите теоретически моменты инерции $I_x$, $I_y$, $I_z$ (см. рисунок выше) бруска с пластинами через его стороны $a$ и $b=с$, толщину металлической пластины $d=1.8~\text{мм}$, а также $M_\text{пл}$, $M_\text{бр}$. Получите систему уравнений, из которой можно будет найти отношение $M_\text{пл}/M_\text{бр}$.

Предоставьте все используемые вами теоретические выкладки и расчеты.

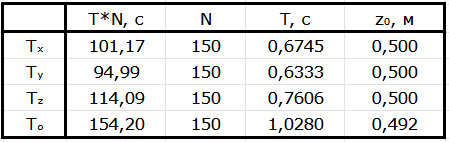
Как известно, для прямоугольника $a$x$b$ момент инерции относительно центра $I_{a\mathrm{x} b} = \cfrac{1}{12} m \left(a^2+b^2 \right)$. Аналогичное выражение верно для момента инерции параллелепипеда относительно оси, проходящей через его центр перпендикулярно граням размера $a\mathrm{x} b$.

$I_y$ складывается из моментов инерции бруска и четырех пластин:
$$I_y = (M_\text{бр}+4M_\text{пл})\cdot \cfrac{1}{12} (a^2+c^2).$$

Для вывода $I_x$ учтем добавку Гюйгенса-Штейнера к моментам инерции пластин. Разобьем их на пары толщины $2d$, центр масс каждой пары находится на расстоянии $\Big(\cfrac{b}{2}+d \Big)$ от оси $x$, тогда:
$$I_x = M_\text{бр}\cdot \cfrac{1}{12}(b^2+c^2) + 4M_\text{пл}\cdot \left( \cfrac{1}{12}\Big(c^2+(2d)^2\Big) + \Big(\cfrac{b}{2}+d \Big) ^2 \right)$$
Как доказано ранее, $T=2\pi\sqrt{\cfrac{I}{m}\cdot \cfrac{z_0}{gRr}}$, т.е.
$$T_0=2\pi\sqrt{\cfrac{I_0}{m_0}\cdot \cfrac{z_0}{gRr}}$$
$$T_x=2\pi\sqrt{\cfrac{I_x+I_0}{M_\text{бр}+4M_\text{пл} + m_0}\cdot \cfrac{z'_0}{gRr}}=
2\pi\sqrt{\cfrac{\cfrac{I_x}{m_0}+\cfrac{I_0}{m_0}}{\cfrac{M_\text{бр}}{m_0}+\cfrac{4M_\text{пл}}{m_0} + 1}\cdot \cfrac{z'_0}{gRr}}$$
$$T_y=2\pi\sqrt{\cfrac{\cfrac{I_y}{m_0}+\cfrac{I_0}{m_0}}{\cfrac{M_\text{бр}}{m_0}+\cfrac{4M_\text{пл}}{m_0} + 1}\cdot \cfrac{z'_0}{gRr}}$$

Объединяем выписанные уравнения в систему:
\begin{equation*}
\begin{cases}
\cfrac{M_\text{бр}}{m_0} \cdot \left( \cfrac{1}{12}(b^2+c^2) -
\left( \cfrac{T_x}{2\pi} \right)^2 \cfrac{gRr}{z'_0} \right)
+ \cfrac{4M_\text{пл}}{m_0} \cdot \left( \left( \cfrac{1}{12}\Big(c^2+(2d)^2\Big) +
\Big(\cfrac{b}{2}+d \Big) ^2 \right) -
\left( \cfrac{T_x}{2\pi} \right)^2 \cfrac{gRr}{z'_0} \right)
=\newline \hspace{24 pt}
= \left( \cfrac{T_x}{2\pi} \right)^2 \cfrac{gRr}{z'_0}
- \left( \cfrac{T_0}{2\pi} \right)^2 \cfrac{gRr}{z_0}
\\
\cfrac{M_\text{бр}}{m_0} \cdot \left( \cfrac{1}{12}(a^2+c^2) -
\left( \cfrac{T_y}{2\pi} \right)^2 \cfrac{gRr}{z'_0} \right)
+ \cfrac{4M_\text{пл}}{m_0} \cdot \left( \cfrac{1}{12}(a^2+c^2) -
\left( \cfrac{T_y}{2\pi} \right)^2 \cfrac{gRr}{z'_0} \right)
=\newline \hspace{24 pt}
= \left( \cfrac{T_y}{2\pi} \right)^2 \cfrac{gRr}{z'_0}
- \left( \cfrac{T_0}{2\pi} \right)^2 \cfrac{gRr}{z_0}
\end{cases}
\end{equation*}

D3  ^0.20 Рассчитайте величину $M_\text{пл}/M_\text{бр}$ численно.

Сделайте это двумя способами:
a) пренебрегая массой и моментом инерции диска и учитывая только брусок с пластинами;
b) учитывая диск.

Сравните результаты этих расчетов. Существенна ли потеря точности при пренебрежением диском?

Начнем с полноценного расчета, т.е. выполним пункт b).
Система уравнений принимает вид
$
\pmatrix{A & B \\ D & E}
\cdot
\pmatrix {M_\text{бр}/m_0 \\ 4M_\text{пл}/m_0}
=
\pmatrix{C \\ F},
$
где коэффициенты рассчитываются следующим образом:
$
A = \left( \cfrac{1}{12}(b^2+c^2) -
\left( \cfrac{T_x}{2\pi} \right)^2 \cfrac{gRr}{z'_0} \right)
= -299\cdot 10^{-6}~\text{м}^2\\
B = \left( \left( \cfrac{1}{12}\Big(c^2+(2d)^2\Big) +
\Big(\cfrac{b}{2}+d \Big) ^2 \right) -
\left( \cfrac{T_x}{2\pi} \right)^2 \cfrac{gRr}{z'_0} \right)
= 44\cdot 10^{-6}~\text{м}^2\\
C = \left( \left( \cfrac{T_x}{2\pi} \right)^2 \cfrac{gRr}{z'_0} -
\left( \cfrac{T_0}{2\pi} \right)^2 \cfrac{gRr}{z_0} \right)
= -769\cdot 10^{-6}~\text{м}^2\\
D = \left( \cfrac{1}{12}(a^2+c^2) -
\left( \cfrac{T_y}{2\pi} \right)^2 \cfrac{gRr}{z'_0} \right)
= -65\cdot 10^{-6}~\text{м}^2\\
E = \left( \cfrac{1}{12}(a^2+c^2) -
\left( \cfrac{T_y}{2\pi} \right)^2 \cfrac{gRr}{z'_0} \right)
= -65\cdot 10^{-6}~\text{м}^2\\
F = \left( \left( \cfrac{T_y}{2\pi} \right)^2 \cfrac{gRr}{z'_0} -
\left( \cfrac{T_0}{2\pi} \right)^2 \cfrac{gRr}{z_0} \right)
= -836\cdot 10^{-6}~\text{м}^2
$

Искомое отношение масс находим, решая систему методом Крамера (либо после расчета чисел $A \dots F$ — подстановкой уравнений друг в друга):
$\cfrac{M_\text{пл}}{M_\text{бр}} \Bigg|_{xy} = \cfrac{1}{4} \cfrac{4M_\text{пл}}{m_0} : \cfrac{M_\text{бр}}{m_0} = \cfrac{1}{4}
\cfrac
{ \begin{vmatrix}
A & C \\ D & F
\end{vmatrix} }

{ \begin{vmatrix}
C & B \\ F & E
\end{vmatrix} }

= \bf{0.573}
$.

Можно по аналогии повторить выкладки, получить выражение
$$I_z =m_\text{бр}\cdot \cfrac{1}{12}(b^2+a^2) + 4m_\text{пл}\cdot \left( \cfrac{1}{12}\Big(a^2+(2d)^2\Big) + \Big(\cfrac{b}{2}+d \Big) ^2 \right)$$ и повторно рассчитать искомое отношение $M_\text{пл}/M_\text{бр}$, опираясь на измерения $T_y$, $T_z$ и $T_0$. Получим
$\cfrac{M_\text{пл}}{M_\text{бр}} \Bigg|_{yz} = \bf{0.564}$.

$\textit{Примечание.}$ Отметим, что обоими способами полученные ответы хорошо сходятся и друг с другом, и со значением, вычисленным с помощью взвешивая частей разобранной установки: $\cfrac{M_\text{пл}}{M_\text{бр}} \Bigg|_\text{взвеш.} = \bf{0.569}$.

Приступим к расчетам для пункта a). Пренебережем $I_0$ и $m_0$ и будем учитывать только брусок.
$$T_x=
2\pi\sqrt{\cfrac{\cfrac{I_x}{m_0}+\cfrac{I_0}{m_0}}{\cfrac{M_\text{бр}}{m_0}+\cfrac{4M_\text{пл}}{m_0} + 1}\cdot \cfrac{z'_0}{gRr}} \xrightarrow[m_0 \to 0; \ I_0 \to 0]{}
2\pi\sqrt{\cfrac{\cfrac{I_x}{m_0}}{\cfrac{M_\text{бр}}{m_0}+\cfrac{4M_\text{пл}}{m_0}}\cdot \cfrac{z'_0}{gRr}}
$$
Такое упрощение формулы соответствует занулению правых частей обоих уравнений в системе: $C=F=0$. Тогда искомое соотношение $\cfrac{M_\text{пл}}{M_\text{бр}} \Bigg|_\text{пренебр.} = \cfrac{1}{4} \cfrac{4M_\text{пл}}{m_0} : \cfrac{M_\text{бр}}{m_0} = -\cfrac{1}{4}\cfrac{A}{B} = \bf{1.69}$ по первому уравнению системы, $\bf{-0.25}$ — по второму уравнению, $\bf{1.24}$ — по измерениям $T_z$.

E1  ^1.00 Проведите точные измерения периода крутильных колебаний зажима. Рассчитайте отношение $\cfrac{I}{m}$. Найдите отношение $m_\text{р}/m_0$.

Предоставьте все используемые вами теоретические выкладки и расчеты. Запишите, какое значение $z_0$ вы выбираете при сборке установки для этой части.

Результаты измерений приведены в таблице. Вычисляем $\cfrac{I}{m} = \left( \cfrac{T}{2\pi} \right) ^2 \cdot \cfrac{gR^2}{z_0} = 1.39 \cdot 10^{-3} ~\text{м}^2$.

Пренебрежем моментом инерции распорок относительно своих осей и будем учитывать их вклад в общий момент инерции только за счет добавок Гюйгенса-Штейнера. Тогда общий момент инерции $I\approx 3m_\text{р} R_\text{р}^2 + m_0 R^2$, где $R_\text{р} = 4.5~\text{см}$ - расстояние от оси зажима до точек крепления распорок, а $R=r$.

Искомое выражение $m_\text{р}/m_0$ можно также выразить через $T$ и рассчитать:
$\cfrac{m_\text{р}}{m_0} = \cfrac{R^2-2\Big( \cfrac{T}{2\pi} \Big) ^2 \cdot \cfrac {gR^2}{z_0}}{3 \Big( \cfrac{T}{2\pi} \Big) ^2 \cdot \cfrac {gR^2}{z_0}-3R_\text{р} ^2} = 0.147$.

$\textit{Примечание.}$ Ответ приблизительно сходится с результатом взвешивания на весах деталей разобранной установки: $\cfrac{m_\text{р}}{m_0} \Bigg|_\text{взвеш.} = 0.19$.

E2  ^1.00 Для каждой из 6 осей в сечении $\alpha$ проведите точные измерения периода колебаний и рассчитайте величину $\cfrac{1}{\sqrt{I/m}}$.

Для каждой из осей на приведенной в листе ответов диаграмме (совпадающей с сечением $\alpha$ и нарисованной с соблюдением пропорции сторон) отложите от центра отрезок, равный $\cfrac{1}{\sqrt{I/m}}$, в обе стороны вдоль направления соответствующей оси. Обведите полученные 12 «внешних» концов отрезков единой замкнутой кривой.

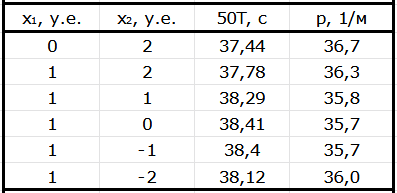
Будем измерять период $N = 50$ колебаний для точности определения $T$. Для идентификации осей вращения будем записывать «декартовы координаты» (номера) точек пересечения оси с поверхностью параллелепипеда (см. диаграмму ниже). По значениям периода и измеренным размерам $R=r = 5.0~\text{см}$ и $z_0 = 46.8~\text{см}$ рассчитаем требуемые величины для нанесения их на диаграмму: $p = \cfrac{1}{\sqrt{I/m}} = \cfrac{2\pi}{T} \cdot \sqrt{\cfrac{z_0}{gR^2}}$.

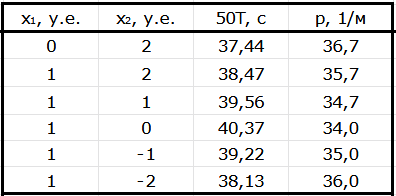
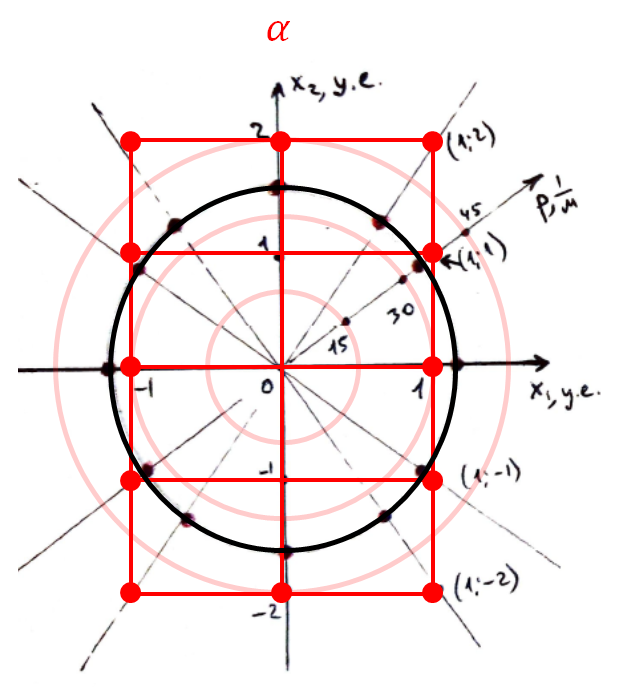
Повторим эту процедуру для плоскостей $\beta$ и $\gamma$.

E3  ^1.00 Повторите аналогичные действия для осей, лежащих в плоскости $\beta$. Приведите все результаты измерений и расчеты. Постройте соответствующую диаграмму в листе ответов.

E4  ^1.00 Повторите аналогичные действия для осей, лежащих в плоскости $\gamma$. Приведите все результаты измерений и расчеты. Постройте соответствующую диаграмму в листе ответов.

F1  ^0.30 Запишите, какое значение $z_0$ вы выбираете при сборке установки. Измерьте и запишите $r_1$ и $r_2$ — внешний и внутренний радиусы шайбы соответственно. Рассчитайте теоретически численное значение величины $\cfrac{I}{m}$ для шайбы.

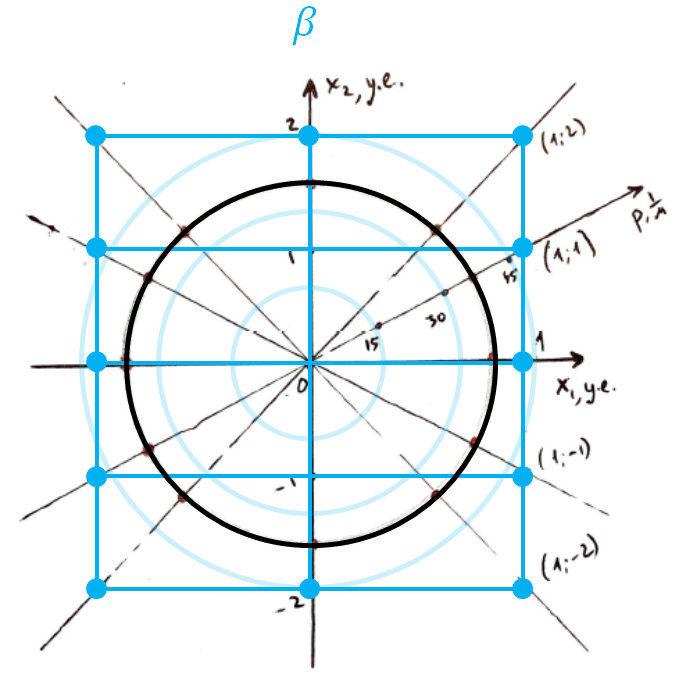
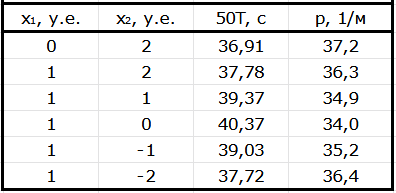
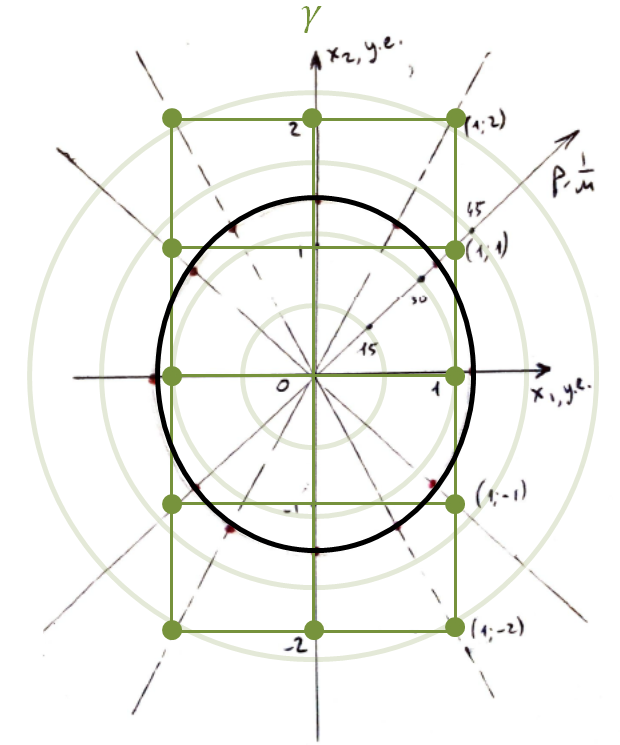
Измеряем величины $z_0 = 46.0~\text{см}, \ r_1 = 1.3~\text{см}, \ r_2 = 3.5~\text{см}$.
Момент инерции шайбы (кольца) можно теоретически рассчитать так ($\rho$ - плотность стали, $h$ - толщина шайбы):
$$\cfrac{I}{m} = \cfrac{\cfrac{\rho (h\pi r_2^2)r_2^2}{2} - \cfrac{\rho (h\pi r_1^2)r_1^2}{2}}{\rho (h\pi r_2^2) - \rho (h\pi r_1^2)} = \cfrac{r_1^2 + r_2^2}{2} = 6.97\cdot10^{-4}~\text{м}^2.$$

F2  ^0.40 Проведите точные измерения периода крутильных колебаний шайбы в воде. Рассчитайте эффективное ускорение свободного падения $g_\text{эфф}$.

Период колебаний выражается прежней формулой: $T=2\pi\sqrt{\cfrac{I}{m}\cdot \cfrac{z_0}{g_\text{эфф}Rr_2}}$. Поэтому $g_\text{эфф} = \cfrac{I}{m} \cdot \cfrac{z_0}{Rr_2} \left(\cfrac{2\pi}{T}\right)^2 = 8.4~\cfrac{\text{м}}{\text{с}^2}$.

$\textit{Примечание.}$ Похожий результат получается, если принять $\rho_\text{шайбы} = \rho_\text{стали} = 7800~\cfrac{\text{кг}}{\text{м}^3}$ и учесть силу Архимеда: $g_\text{эфф} = \cfrac{\rho_\text{стали} - \rho_\text{воды}}{\rho_\text{стали}} = 8.6~\cfrac{\text{м}}{\text{с}^2}$.

F3  ^1.30 Решите теоретическую задачу. Пусть тонкая шайба с внутренним и внешним радиусами $r_1$ и $r_2$ соответственно колеблется в толще воды, за счет вязкого трения приводя в движение с некоторыми скоростями слои воды на глубинах от $(H-h)$ до $(H+h)$, где $H$ — глубина погружения шайбы, $h$ — условная суммарная толщина движущихся слоёв. Вязкость воды $\eta=8.9\cdot 10^{-4}~\text{Па}\cdot\text{с}$, ускорение свободного падения $g=9.81~\text{м} / \text{с}^2$.

Какой момент сил вязкого трения $M$ действует на шайбу в момент, когда она вращается с угловой скоростью $\dot{\varphi}$? Выразите $M$ через $\dot{\varphi}$, $\eta$, $h$, $r_1$, $r_2$.

Выразите логарифмический декремент затухания $d$ колебаний с вязким трением через $\eta$, $h$, $r_1$, $r_2$, $m$, $T$.

Пусть вода вращается «слоями»: угловая скорость $\omega$ одна общая для всего слоя и линейно убывает с высотой от $\omega(0) = \dot \varphi$ до $\omega(h)=0$ (симметрично сверху и снизу от шайбы).

Выделим на верхней поверхности шайбы кольцо радиуса $r$ и ширины $dr$. Момент сил сопротивления, действующих на него, равен $dM = r \cdot \eta \cdot 2\pi rdr \cdot \cfrac{\dot \varphi r}{h}$, а (с учетом нижней поверхности шайбы) полный момент сил $M = 2 \int \limits_{r_1}^{r_2} r \cdot \eta \cdot 2\pi rdr \cdot \cfrac{\dot \varphi r}{h} = \cfrac{4\pi \eta \dot \varphi}{h} \int \limits_{r_1}^{r_2} r^3dr = \dot \varphi \cdot \cfrac{\eta\pi (r_2^4-r_1^4)}{h}$.

Известно, что уравнение вида $\ddot \varphi + 2\gamma\dot\varphi + \omega_0^2 \varphi = 0$ имеет решение вида $\varphi(t) = \varphi_0 \cdot e^{-\gamma t} \cdot \cos\left(\sqrt{\omega_0^2 - \beta^2}\cdot t + \psi\right)$. Логарифмический декремент вычисляется в таком случае следующим образом: $d=\text{ln}\cfrac{\varphi_i}{\varphi_{i+1}} = \ln (e^{\gamma T}) = \gamma T$, где $T = \cfrac{2\pi}{\omega} \approx \cfrac{2\pi}{\omega_0}$ - период колебаний.

В нашем случае уравнение колебаний с учетом вязкости принимает вид $I\ddot \varphi + \cfrac{\eta\pi (r_2^4-r_1^4)}{h}\dot\varphi + mg\cfrac{Rr}{z_0} \varphi = 0$. Поэтому $d = \gamma T = \cfrac{\eta\pi (r_2^4-r_1^4)}{2Ih} T = \cfrac{\eta\pi (r_2^4-r_1^4)}{2m\cfrac{r_1^2 + r_2^2}{2}h} T = \cfrac{T\eta\pi (r_2^2-r_1^2)}{hm}$.

F4  ^1.00 Как вы заметили, колебания довольно быстро затухают. Пусть $\varphi(i)$ - амплитуда $i$-го колебания. Снимите зависимость $\varphi(i)$. Возможно, для этого потребуется несколько раз запускать колебания с одинаковыми начальными условиями. Постройте линеаризованный график и по нему рассчитайте логарифмический декремент затухания $d$.

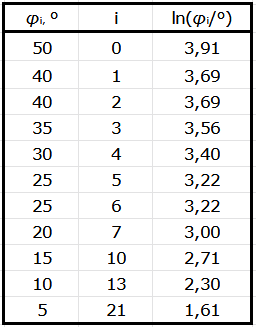
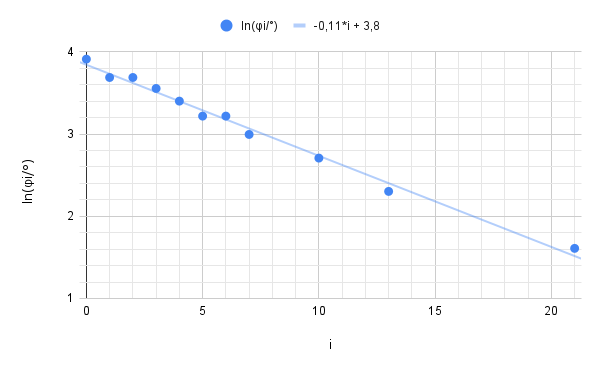
Определение логарифмического декремента $d=\text{ln}\cfrac{\varphi_i}{\varphi_{i+1}}$ преобразуется к выражению $\ln\varphi_i = \ln\varphi_0 - id$. Поэтому график $\ln \varphi_i (i)$ должен быть линейным с коэффициентом $(-d)$.

По коэффициенту наклона построенного линеаризованного графика определяем $d = 0.11$.

F5  ^0.30 Используя $d$, оцените толщину $h$ движущихся слоёв воды.

Ранее получено выражение $d= \cfrac{T\eta\pi (r_2^2-r_1^2)}{hm}$. Воспользуемся измеренными и рассчитанными величинами, а также приведенным в условии значением $m = 80~\text{г}$, чтобы рассчитать $h = \cfrac{T\eta\pi (r_2^2-r_1^2)}{md} = 0.31~\text{мм}$.

$\textit{Примечание.}$ Отметим, что в условии была намеренно указана $m = 80~\text{г}$ вместо настоящего значения $120~\text{г}$. Это было сделано для отсечения возможности успешно решить часть C простым взвешиванием гаек на рычаге. Если в расчетах учесть настоящее значение $m$, получится несколько другая оценка: $h = 0.21~{мм}$.

G0  ^?? Запишите, какое значение $z_0$ вы выбираете при сборке установки. Если вы не делали пункт F1, сделайте его сейчас.

G1  ^0.40 Проведите точные измерения периода крутильных колебаний шайбы над доской с магнитами. Рассчитайте эффективное ускорение свободного падения $g_\text{эфф}$.

G2  ^1.00 Как и в предыдущей части, колебания затухающие. Снимите зависимость $\varphi(i)$. Возможно, для этого потребуется несколько раз запускать колебания с одинаковыми начальными условиями. Постройте линеаризованный график и по нему рассчитайте логарифмический декремент затухания $d$.

G3  ^0.30 Рассчитайте численно коээфициент пропорциональности в соотношении $M_\text{маг. тр.}=k\cdot \omega$ между моментом сил магнитного трения и угловой скоростью.

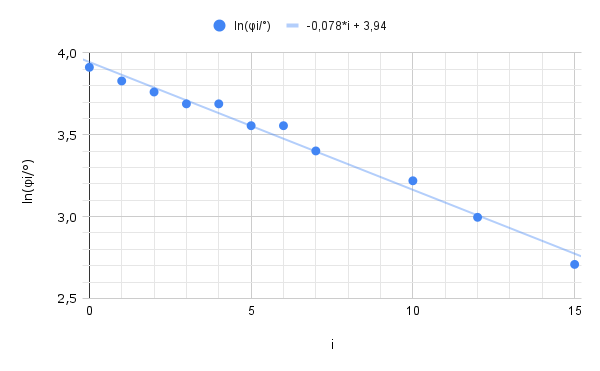
Уравнение колебаний на этот раз выглядит так: $I\ddot \varphi + k\dot\varphi + mg\cfrac{Rr}{z_0} \varphi = 0$. Логарифмический декремент соответствует величине $d=\cfrac{k}{2I}T$. Поэтому коэффициент $k$ можно выразить и рассчитать следующим образом: $k = \cfrac{d\cdot 2I}{T} = \cfrac{2d\cfrac{I}{m}m}{T} = 1.24\cdot 10^{-5}\cfrac{\text{кг}\cdot \text{м}^2}{\text{с}}$.

$\textit{Примечание.}$ Как и в части F, это значение на самом деле надо скорректировать, если учитывать настоящую $m = 120~\text{г}$: тогда $k = 1.87\cdot 10^{-5}\cfrac{\text{кг}\cdot \text{м}^2}{\text{с}}$.